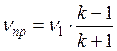Расчёт скорости ударной волны

Для простоты и наглядности вывода соотношений для фронта прямой ударной волны представим себе, что в трубу (рисунок 4.2) площадью поперечного сечения 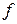, заполненную сжимаемой средой, с постоянной скоростью 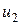вдвигается поршень.

Среду будем считать идеальной, а процесс адиабатным. В момент времени 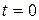в сечении 0 - 0 поршень мгновенно начал двигаться с постоянной скоростью 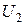. При этом от поршня начнет распространяться фронт ударной волны 2 - 2 со скоростью 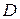. Среда перед фронтом ударной волны имеет параметры 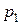, , 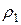, 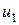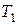. За фронтом ударной волны (зона 1-1 - 2-2) параметры обозначим , , , .

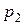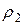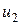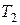Для того, чтобы найти связь между параметрами среды до и после фронта ударной волны, воспользуемся законами сохранения массы, импульса и энергии.

За время 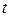поршень относительно невозмущенного газа пройдет расстояние 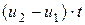, а фронт ударной волны – на расстояние 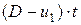. Масса ударно сжатого газа равна 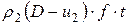; с другой стороны, эта масса до сжатия определяется величиной 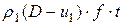. Приравнивая эти выражения, получим

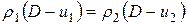. (4.5)

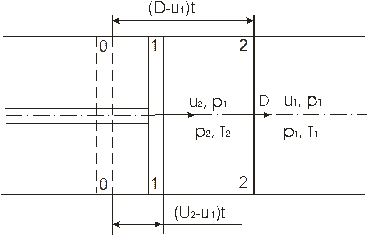
Рисунок 4.2 – К выводу зависимостей на фронте ударной волны

Поскольку изменение количества движения данной массы равно импульсу действующей на нее силы, то получим:

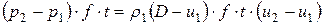
или

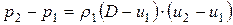. (4.6)

Составим теперь уравнение сохранения энергии. Для адиабатного процесса изменение полной энергии среды равно произведенной над ней работе. Обозначим внутреннею энергию единицы массы среды через 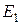, а кинетическую энергию через 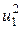/2. Следовательно, полная энергия невозмущенной среды будет равна:

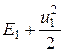, (4.7)

а полная энергия ударно сжатой среды:

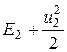. (4.8)

Полное изменение энергии среды равно работе внешних сил:

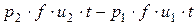, (4.9)

поэтому

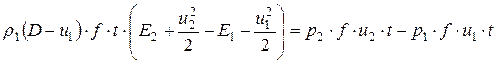. (4.10)

Это уравнение сохранения можно записать в виде:

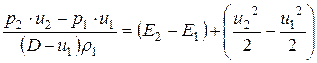. (4.11)

Преобразуем выведенное соотношение. Напишем уравнение (4.6) в виде:

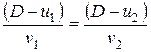. (4.12)

Здесь 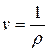- удельный объем. Умножив обе части этого уравнения на 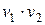, получим:

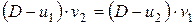, (4.13)

откуда

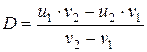. (4.14)

Вычитая 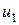из обеих частей равенства, найдем:

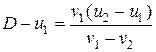, (4.15)

откуда

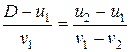. (4.16)

Далее из (4.6) имеем

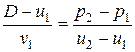. (4.17)

Сравнивая два последних выражения, получим:

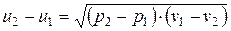. (4.18)

Из найденных выражений легко получается скорость распространения ударной волны:

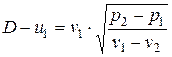. (4.19)

Если среда перед фронтом покоится, т.е. 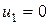, то

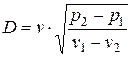. (4.20)

Весьма важное значение в теории ударных волн имеет адиабата Гюгонио, устанавливающая связь между параметрами среды до и после прохождения через нее скачка уплотнения. Изобразив эту связь в виде диаграммы в координатах 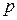, , 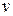мы получим так называемую кривую Гюгонио (рисунок 4.3).

P

Ударная адиабата

		V

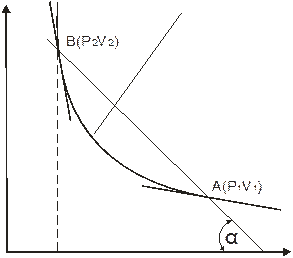
Рисунок 4.3 – Адиабата Гюгонио

Используя эту диаграмму, можно в простой и наглядной форме исследовать некоторые особенности ударных волн. Проведём через точку 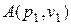, характеризующую состояние невозмущенной среды, и точку 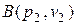, характеризующую состояние среды, сжатой ударной волны, прямую. Очевидно, что 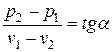, где 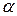- угол наклона этой прямой к оси абсцисс. Таким образом, очевидно, что величины 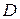и 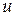целиком определяются углом наклона .

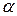Для ударных волн всегда 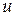> 0, причем 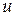< 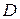, т.е. среда перемещается в направлении распространения фронта, но с меньшей, чем у фронта скоростью.

4.8 Контрольные вопросы

4.8.1 В чем принципиально заключается отличие физического взрыва от химического?

4.8.2 Классификация взрывчатых веществ.

4.8.3 Как определяется кислородный баланс взрывчатого вещества?

4.8.4 В чем заключается тепловая и нетепловая теории механического воздействия на взрывчатые системы?

4.8.5 В чем различие между электроогневыми и электрическими способами взрывания?

4.8.6 Как устроен детонационный шнур?

4.8.7 Какие величины на адиабате Гюгонио определяется углом наклона α ?

4.8.8 Какие законы используются при выводе скорости ударной волны?

Детонация

Взрыв вызывается ударной волной. Если в каком-либо слое вещества резко повышается давление, то от этого места начинает распространяться фронт повышенного давления. Эта волна приводит к значительному скачку температуры, который передается от слоя к слою. Повышение температуры дает начало взрывной реакции, а взрыв приводит к повышению давления и поддерживает ударную волну, интенсивность которой иначе быстро падала бы по мере ее распространения. Таким образом, ударная волна вызывает взрыв, а взрыв в свою очередь поддерживает ударную волну. Такой взрыв и называется детонацией.

Детонация - это процесс химического превращения взрывчатого вещества, сопровождающийся выделением теплоты и распространяющийся с постоянной скоростью, превышающей скорость звука в данном веществе.

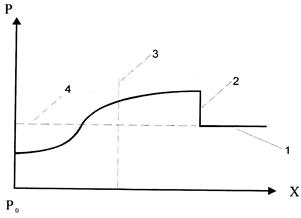
1 - зона исходного вещества; 2 - фронт волны; 3 - зона химической реакции; 4 – зона продуктов детонации; Р_о – начальное давление; X - простран­ственная координата.

Рисунок 5.1 - Распределение давления в детонационной волне

В отличие от горения, где распространение пламени обусловлено мед­ленными процессами диффузии и теплопроводности, детонация представля­ет собой комплекс мощной ударной волны и следующей за её фронтом хи­мические превращения вещества (детонационная волна).

Ударная волна сжимает и нагревает взрывчатое вещество, вызывая в нём реакцию, продукты которой сильно расширяются, т.е. создаются условия взрыва.