Влияние температуры на скорость химической реакции
Скорость химической реакции зависит от температуры. Влияние температурына скорость химической реакции определяется либо приближённым эмпирическим уравнением Вант-Гоффа, либо более точным уравнением Аррениуса.
Согласно правилу Вант-Гоффа при повышении температуры на 10° скорость химической реакции (или константа скорости) увеличивается в одно и то же число раз
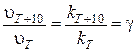 ,
, 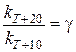 и т.д.;
и т.д.; 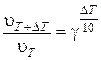 ,
, 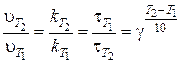 . (1)
. (1)
В этих формулах 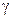 – температурный коэффициент, который для большинства низкотемпературных реакций изменяется в пределах от 2 до 4. Он показывает, во сколько раз увеличится скорость реакции при повышении температурына каждые 10°;
– температурный коэффициент, который для большинства низкотемпературных реакций изменяется в пределах от 2 до 4. Он показывает, во сколько раз увеличится скорость реакции при повышении температурына каждые 10°; 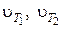 – скорости реакции при соответствующих температурах Т1 и Т2;
– скорости реакции при соответствующих температурах Т1 и Т2; 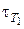 ,
, 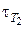 – время протекания реакции при данных температурах.
– время протекания реакции при данных температурах.
Уравнение Аррениуса в виде интегральных уравнений
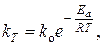
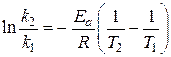 (2)
(2)
позволяет определять энергию активации данной реакции.
Пример 4. Как изменится скорость реакции, протекающей в газовой фазе, при повышении температуры от 20 до 60 °С, если γ = 2?
Решение. Используем выражение (1), в которое подставляем данные: T1 = 20 °С; T2 = 60 °C; γ = 2. Получаем
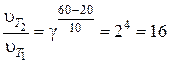 ,
,
т.е. при повышении температуры на 40°С скорость реакции возросла в 16 раз.
Пример 5. Некоторая реакция в газовой фазе при 100 °С заканчивается за 27 с. За сколько секунд закончится та же реакция при температуре 130 °С, если γ = 3?
Решение. Время протекания реакции обратно пропорционально скорости реакции. Поэтому в выражении (1) используем вместо скорости время. Подставляем 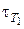 = 27с, Т1 = 100 °С, а
= 27с, Т1 = 100 °С, а 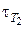 – время, необходимое для протекания реакции при Т2 = 130 °С, γ = 3, тогда
– время, необходимое для протекания реакции при Т2 = 130 °С, γ = 3, тогда
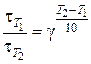 ,
, 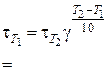 , 27 =
, 27 = 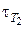 ·
· 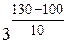 = 27 ·
= 27 · 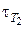 .
.
Отсюда 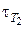 =
= 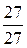 = 1с, т.е. при температуре 130 °С реакция закончится за 1с.
= 1с, т.е. при температуре 130 °С реакция закончится за 1с.
Химическое равновесие
Обратимая химическая реакция протекает не до полного расходования исходных веществ (или хотя бы одного из них), а до состояния химического равновесия, когда в реакционной системе присутствуют все участники химической реакции. Под химическим равновесием понимают такое состояние системы, когда скорость прямой реакции равна скорости обратного процесса.
Количественно характеристики равновесного состояния химической реакции определяются константами равновесия, выраженными через равновесные давления (pi) или равновесные молярные концентрации участников реакции (ci).
В общем случае для любой газовой реакции
a А + b B ↔ е Е + d D
константы равновесия определяются следующими выражениями, которые называются законом действующих масс:
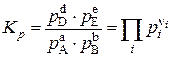 ,
, 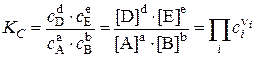 .
.
Соотношение между так определяемыми константами равновесия устанавливаются с использованием выражения 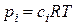 и имеет вид
и имеет вид 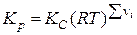 ,
, 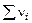 = d + e – a – b. Если давления ( p) определять в атм, а концентрацию в моль/л, то в этой формуле R = 0,082 л×атм/моль×K.
= d + e – a – b. Если давления ( p) определять в атм, а концентрацию в моль/л, то в этой формуле R = 0,082 л×атм/моль×K.
Для гетерогенных реакций между чистыми конденсированными (твердыми или жидкими) веществами и газовыми смесями закон действующих масс записывается только с учетом количественных характеристик равновесной газовой фазы. Константы равновесия не зависят от исходных концентраций реагирующих веществ и зависят только от температуры.
Пример 6. Напишите выражения констант равновесия 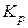 и
и 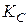 для следующих реакций:
для следующих реакций:
1) СO2 (г) + H2 (г) ↔ CO (г) + H2O (г);
2) С (к) + CO2 (г) ↔ 2CO (г).
Решение. Константы равновесия 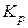 и
и 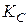 для реакции 1:
для реакции 1:
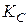
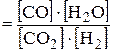 ;
; 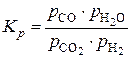 ,
,
для реакции 2: 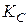
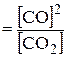 ;
; 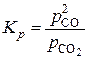 .
.
Вещество C (к) находится в твердом состоянии и его концентрация в уравнение закона действующих масс не входит.
Пример 7. При нагревании водорода и йода в замкнутом сосуде протекает реакция H2 (г) + I2 (г) ↔ 2HI (г). Равновесная смесь содержит 5,64 моль/л HI, 0,12 моль/л I2 и 5,28 моль/л Н2. Вычислите константу равновесия указанной реакции и исходные концентрации Н2 и I2.
Решение. Данная реакция идёт без изменения объема, и значение константы равновесия будет одинаково при всех способах выражения концентраций. Поэтому можно записать 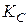 =
= 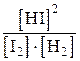 , подставив равновесные концентрации веществ, получим
, подставив равновесные концентрации веществ, получим 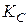 =
= 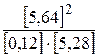 = 50,19.
= 50,19.
Определяем исходные концентрации йода и водорода. По реакции для образования 2 моль HI расходуется 1 моль Н2 и 1 моль I2. К моменту достижения равновесия для получения 5,64 моль/л HI прореагировало 5,64/2 моль I2 и 5,64/2 моль Н2. По условию задачи в равновесной смеси осталось непрореагировавшими 0,12 моль/л I2 и 5,28 моль/л Н2. Находим исходные концентрации этих веществ:
[I2]o = 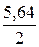 + 0,12 = 2,94 моль/л; [H2]o =
+ 0,12 = 2,94 моль/л; [H2]o = 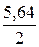 + 5,28 = 8,1 моль/л.
+ 5,28 = 8,1 моль/л.
Пример 8. Константа равновесия 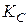 реакции FeO (к) + СО (г) ↔ Fe (к) + СО2 (г) при 1000 °С равна 0,5. Каковы равновесные концентрации СО и СО2, если начальные концентрации этих веществ составляли: [CO]o = 0,05 моль/л; [СО2]o = 0,01 моль/л?
реакции FeO (к) + СО (г) ↔ Fe (к) + СО2 (г) при 1000 °С равна 0,5. Каковы равновесные концентрации СО и СО2, если начальные концентрации этих веществ составляли: [CO]o = 0,05 моль/л; [СО2]o = 0,01 моль/л?
Решение. До взаимодействия было 0,05 моль СО и 0,01 моль СО2. К моменту равновесия в реакцию вступило х молей СО. Тогда,согласно уравнению реакции, образовалось х молей СО2. Таким образом, к моментудостиженияравновесия, равновесные концентрации [СО] = (0,05 – х) моль/л, [СО2] = (0,01+ х) моль/л.
Отсюда 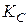 =
= 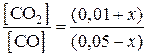 . Подставивв это выражение
. Подставивв это выражение 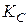 = 0,5, получим х = 0,01, а [СО] = 0,05 – 0,01 = 0,04 моль/л, [СО2]= 0,01 + 0,01 = 0,02 моль/л.
= 0,5, получим х = 0,01, а [СО] = 0,05 – 0,01 = 0,04 моль/л, [СО2]= 0,01 + 0,01 = 0,02 моль/л.
