Моделирование пожаров и взрывов
Чтобы реально оценить пожарный риск на том или ином объекте защиты, необходимо познать закономерности возникновения, развития и ликвидации пожара.
Действительно, начиная со второй половины ХХ века, всё больше исследователей в разных странах мира начинают профессионально изучать пожары. Наука о пожаре занимает своё место среди других прикладных наук. Трудно указать научную дисциплину, методы которой не использовались бы при решении проблем пожарной безопасности.
В каком-то помещении возник пожар. Нарастает количество выделяемого тепла, растет температура, появляются продукты горения. Часть тепла рассеивается в виде продуктов горения в окружающем пространстве. Другая часть аккумулируется горючими и негорючими материалами, находящимися в помещении. Нагреваясь до определенной температуры, сгораемые конструкции,
предметы и оборудование воспламеняются и горят, а несгораемые материалы и конструкции меняют свойства, теряя механическую прочность, и при определенных условиях разрушаются. Пожар может распространяться на соседние помещения, охватить весь объект, перебросится на соседние здания.
Чтобы проанализировать все перечисленные явления и процессы, необходимо использовать методы общей физики, химии, теплофизики, механики твердых тел, жидкостей и газов, токсикологии, физиологии, психологии, математики и других научных дисциплин. Только с помощью указанных дисциплин можно изучить и описать все сложнейшие явления, сопровождающие возникновение, развитие и ликвидацию пожара, т.е. смоделировать пожар, построить его модель.
Понятие модели является центральным в современной теории познания.
В процессе познавательной деятельности человека постепенно вырабатывается система представлений о тех или иных свойствах изучаемого объекта и их связях. Эта система представлений закрепляется, фиксируется в виде описания объекта на обычном языке, в виде рисунка, схемы, графика, формулы, в виде макетов, механизмов, технических устройств. Всё это обобщается в едином понятии «модель», а исследование объектов познания на их моделях называется моделированием.
Модель – это создаваемый объект, на который воспроизводятся вполне определенные характеристики реального исследуемого объекта с целью его изучения.
Метод моделирования, как метод научного познания, имеет историю, исчисляемую тысячелетиями. Его нельзя считать недавно открытым. Однако только в середине ХХ века само моделирование стало предметом как философского, так и специальных исследований. Объясняется это тем, что метод моделирования переживает сейчас подлинную революцию, связанную с развитием теории подобия, кибернетики и электронной вычислительной техники.
Это и позволило в последние годы приступить к созданию и активному использованию, прежде всего в научных целях, а затем на практике различных моделей возникновения, развитие и тушение пожаров.
В первой половине ХХ века возникла острая необходимость в развитии специфической теории физического моделирования в связи с интенсивным развитием авиастроения и кораблестроения. Так как сформировалась теория подобия, зачатки которой появились задолго до нашего века.
Теория подобия – это учение об условиях подобия физических явлений, процессов и систем, которая опирается на учение о размерностях физических величин и положено в основу экспериментов с физическими моделями. Физические явления, процессы и системы считаются подобными, если в сходственных точках пространства в сходственные моменты времени величины, характеризующие состояние системы, пропорциональны соответствующим величинам другой системы. Такими величинами являются так называемые критерии подобия – безразмерные числовые характеристики, составленные из размерных физических параметров, определяющих исследуемые физические явления. Равенство однотипных критериев подобия для двух физических процессов и систем – необходимое и достаточное условие их физического подобия. Предметом теории подобия является установление критериев подобия для различных физических явлений. Автором теории физического моделирования процессов теплопередачи и тепловых устройств является М. В. Кирпичёв (1879-1955г.г.). Теория подобия в целом и его работы послужили импульсом в использовании методов физического моделирования при изучении динамики пожаров.
Во многих моделях пожаров используется так называемые уравнения Навье-Стокса, т.е. дифференциальные уравнения движения вязкой жидкости или газа, представляющих математическое выражение законов сохранения импульсов и массы. Впервые уравнения Навье-Стокса вывел в 1822 г. французский ученный Анри Навье (несколько позже это сделал С.Д. Пуассон, затем англичанин Стокс).
Использование ЭВМ позволило эффективно применять эти численные методы решения уравнений Навье-Стокса, но и ЭВМ во многих случаях пока не в состоянии решать с нужной степенью точности такие задачи.
Модель – это объект любой природы, который заменяет реальный исследуемый объект так, что его изучение дает реальную информацию о реальном объекте.
Различают материальное (предметное) и идеальное (абстрактное) моделирование. Материальным называется моделирование, в котором исследование ведется на основе модели, воспроизводящей основные геометрические, физические, динамические и функциональные характеристики изучаемого объекта.
Идеальные модели связаны с использованием каких-либо символических схем (графических, логических, математически и др.). Для изучения пожаров используют математические модели, которые подразделяются на аналитические и имитационные. В случае аналитических моделей исследуемый объект и его свойства описывают отношениями – функциями (дифференциальными и интегральными уравнениями).
Одной из первых и простейших аналитических моделей пожара была модель, используемая при испытании строительных конструкций на огнестойкость. Её обычно называют стандартной кривой «температура - время» и задают в виде таблицы, либо в виде эмпирической формулы:
 (6.1)
(6.1)
где 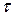 - время, мин;
- время, мин;
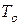 - начальная температура, o C;
- начальная температура, o C;
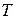 - текущая температура пожара, o C.
- текущая температура пожара, o C.
Впервые в виде таблицы эта зависимость была выведена в 1916 г. в результате наблюдений за температурой пожаров древесины. С тех пор изменялась лишь незначительно и в 1966 г. была рекомендована Международной организацией по стандартизации в качестве температурного режима для испытаний строительных конструкций на огнестойкость.
Имитационные методы представляют собой совокупность программ ЭВМ, с помощью которых воспроизводятся алгоритмы и процедуры, описывающие свойства и динамику интересующего нас процесса. Имитационные модели обычно используют в тех случаях, когда не удается построить для изучаемого объекта достаточно простых и удобных для исследования аналитических моделей.
Возвращаясь к основному объекту нашего изучения – пожару, заметим, что мы дали словесное описание возникновения и развития пожара в помещении. Это описание уже является простейшей моделью пожара, которую называют вербальной. Углубляя это описание пожара, мы постепенно будем его детализировать и уточнять. Эти ситуации удобно описывать в терминах физических полей. Например, в ситуации «помещение до пожара, помещение во время пожара» приходиться анализировать температурные поля, поля концентрации газа и дыма, поля давлений, скоростей газовых потоков и т.д.
Очевидно, с математической точки зрения задание поля означает задание функции точки. Например, нестационарное температурное поле в помещении при пожаре можно описать некоторой функцией:
 ,
,
 где
где 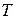 - температура;
- температура;
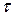 - время;
- время;
 - декартовые координаты точки.
- декартовые координаты точки.
В таком случае, наиболее полной и точной моделью пожара в помещении является задание всех физических полей, существующих в нём до пожара, во время пожара на всех его стадиях и после ликвидации. Знание этих полей позволяет правильно сконструировать и разместить в помещениях пожарные датчики разных типов (тепловые, дымовые и др.), правильно спроектировать само здание с учётом нужной степени огнестойкости его конструкции, обеспечение путей эвакуации и т.д.
Следовательно, центральной проблемой математического моделирования пожаров является разработка способов и методов получения всех характеристик его физических полей. Такие математические модели пожаров называют полевыми (дифференциальными) моделями.
Эти модели основываются на использовании известных уравнений механики сплошной среды, включающих в себя реологический закон Стокса, закон теплопроводности Фурье, законы диффузии, законы радиационного переноса в газовой среде и т.п. Однако, эта система уравнений, описывающих изменение во времени плотности, температуры и состава газовой смеси в каждой точке пространства внутри помещения, достаточно громоздка и её численное решение даже с помощью современных высокопроизводительных ЭВМ связано с большими трудностями. Существуют и другие проблемы, ограничивающие практическое использование полевых (дифференциальных) моделей (например, недостаточная изученность явления турбулентности, которую необходимо учитывать в этих моделях).
Несмотря на перечисленные сложности в развитии и использовании полевых моделей пожара, их совершенствованию уделяется большое внимание, как в нашей стране, так и за рубежом.
Хотя полевые модели пожара в принципе позволяют получить наиболее полную и точную информацию об исследуемом процессе по сравнению с другими математическими моделями пожара, однако не для всех прикладных пожарно-технических задач необходима такая детальная информация. Поэтому во многих случаях на практике используются и другие, более простые, математические модели пожара, среди которых нужно отметить интегральные модели. Эти модели описывают изменение среднеобъёмных параметров состояния газовой среды (плотности, давления, температуры, концентрации различных компонентов среды) во времени при пожаре в помещении.
Усреднение всех этих параметров теоретически осуществляется с помощью интегральной теоремы о среднем, на практике – экспериментально, расчетным путем. Далее, на основе сохранения массы и первого закона термодинамики составляется так называемое уравнение пожара: уравнение материального баланса, уравнение кислородного баланса, уравнение продуктов горения, уравнение баланса инертного газа, уравнение энергии пожара. К этим уравнениям добавляется усредненное уравнение состояния среды, находящейся в помещении при пожаре, которое связывает среднеобъемную температуру со среднеобъёмным давлением и плотностью.
Совокупность всех этих соотношений (обыкновенные дифференциальные уравнения первого порядка) обеспечивает математическое описание пожара в помещении на уровне усредненных термодинамических параметров состояния среды. Именно эти соотношения и называют интегральной моделью пожара в помещении.
Проблема защиты от взрывов напрямую связана с проблемой противопожарной защиты. Зачастую пожары сопровождаются взрывами или инициируются ими. Моделирование динамики взрыва необходимо для прогнозирования развития аварийной ситуации и предотвращения её катастрофических последствий.
В настоящее время в мире существуют десятки моделей пожаров, разработанных специалистами Австралии, Великобритании, Германии, Канады, России, США, Швеции, Японии и др. стран.
