Химическая термодинамика

Химическая термодинамика рассматривает энергетические аспекты различных процессов и определяет условия их самопроизвольного протекания.

Химическая термодинамика является уникальной теорией; рассматривая только макроскопические свойства вещества может предсказать возможное поведение системы и ответить на вопрос: возможна ли химическая реакция (физико-химический процесс) в данных условиях или нет.

Первое начало (первый закон) термодинамики – это всеобщий закон природы, закон сохранения и превращения энергии, соответствующий основному положению диалектического материализма о вечности и неуничтожимости движения. Впервые этот закон в 1842 г. сформулировал выдающийся немецкий физик Ю. Мейер, врач по образованию.

Энергия не исчезает и не возникает из ничего, а только превращается из одного вида в другой в строго эквивалентных соотношениях.

В зависимости от вида системы первый закон термодинамики имеет различные формулировки.

В изолированной системе внутренняя энергия постоянна, т.е. ∆U = 0.

Для закрытой системы:

Если к закрытой системе подвести теплоту, то эта энергия расходуется на увеличение внутренней энергии системы и на совершение системой работы против внешних сил окружающей среды.

Математическое выражение первого закона термодинамики в интегральной форме имеет вид: Q = ΔU + W (1).

Здесь: ΔU – изменение внутренней энергии. Внутренняя энергия представляет собой общий запас энергии системы за вычетом кинетической энергии движения центра масс и потенциальной энергии системы. Этот общий запас включает энергию поступательного и вращательного движения молекул, энергию колебательного движения атомов и атомных групп, составляющих молекулы, энергию взаимодействия ядер и электронов, энергию взаимодействия нуклонов в ядре.

Абсолютное значение внутренней энергии не известно, т.к. не возможно перевести систему в состояние, где внутренняя энергия была бы равна нулю. Поэтому в термодинамических расчетах пользуются разностными значениями внутренней энергии (∆U). Измеряется внутренняя энергия в Дж или Дж/моль.

Теплота Q и работа W. Это две формы передачи энергии к системе и наоборот. Работа характеризует направленную передачу энергии, а теплота – хаотическую. Эти функции характеризуют не состояние, а процесс передачи энергии, и являются функциями процесса или функциями пути. Измеряются они в Дж или в Дж/моль. Теплота, переданная системе в ходе процесса, является отрицательной (теплота поглощается, Q < 0)), а такой процесс называется эндотермическим. Экзотермическим называется процесс, в котором теплота выделяется (передается от системы к окружающей среде). В этом случае теплота положительная (Q > 0).

Для системы идеального газа в зависимости от протекаемого процесса математический вид первого закона термодинамики меняется:

1. Для изотермического процесса (Т = const) ΔU = 0 и Q = W (2).

2. Для изохорного процесса (V=const) W=0 и Q_V =ΔU:

3. Для изобарного процесса (р=const).

Q_р = ΔU + рΔV = (U_кон – U_нач) + (рV_кон – рV_нач) = (U_кон - рV_кон) – (U_нач – рV_нач).

Сумма внутренней энергии системы и произведения объема на давление (U + рV) называют энтальпией (Н). Поэтому Q_р = ΔU + рΔV = Δ Н.

Энтальпия Н – это функция специально введенная в термодинамику, которая характеризует общий запас энергии системы при постоянном давлении (внутренняя энергия – при постоянном объеме). Абсолютное ее значение не известно, поэтому в расчетах используют ∆Н. Измеряется энтальпия в Дж или Дж/моль.

Энтальпия является функцией состояния системы. Одним из самых важных свойств функций состояния является следующее: при переходе системы из одного состояния в другое изменение функции состояния не зависит от пути перехода (процесса), а определяется лишь начальным и конечным её состояниями. К ним относят внутреннюю энергию U [Дж], энтальпию H [Дж], энтропию S [Дж/К], энергию Гиббса G [Дж], энергию Гельмгольца A [Дж].

Энтальпия системы является экстенсивным параметром и зависит от количества вещества, температуры и давления, поэтому изменение энтальпии в результате химической реакции или других процессов определяют при стандартных условиях.

Стандартные условия: количество вещества – 1 моль;

давление – 1 атм. = 760 мм рт. ст. = 101325 Па; температура – 298 К ≈ 25⁰С.

В термодинамики для оценки энергетического состояния веществ используют значения стандартных энтальпий образования этих веществ, обозначаемые ∆Н⁰_обр, кДж/моль и стандартных энтальпий сгорания - ∆Н⁰_сг, кДж/моль.

Стандартная энтальпия образования простых веществ в их наиболее термодинамически устойчивом агрегатном и аллотропном состоянии при стандартных условиях принимается равной нулю.

Например, для кислорода ∆Н⁰_обр(О₂) = 0, для графита ∆Н⁰_обр(С_{графита}) = 0. Однако стандартная энтальпия образования озона ∆Н⁰_обр(О₃) = 142,2 кДж/моль, алмаза ∆Н⁰_обр(С_алмаз) = 1,8 кДж/моль.

Стандартная энтальпия образования сложных веществ равна энтальпии реакции получения 1 моль этого вещества из простых веществ при стандартных условиях.

Например, стандартная энтальпия образования этанола равна стандартной энтальпии гипотетической реакции: 2С_графит + 3Н₂(г) + 0,5О₂(г) = С₂Н₅ОН (ж), ∆Н⁰_f(С₂Н₅ОН) = -277 кДж/моль.

Стандартная энтальпия сгорания простейших (высших) оксидовв их наиболее устойчивых состояниях равна нулю.

Например, для воды ∆Н⁰_сг(Н₂О(ж)) = 0; для углекислого газа ∆Н⁰_сг(СО₂(г)) = 0 и т.д.

Стандартная энтальпия сгорания сложных веществ равна энтальпии реакции сгорания в атмосфере кислорода 1 моль вещества при стандартных условиях до простейших оксидов. При этом все участники реакции должны быть в устойчивых агрегатных состояниях.

Например, стандартная энтальпия сгорания этанола равна стандартной энтальпии реакции: С₂Н₅ОН + 7/2О₂ = 2СО₂ + 3Н₂О, ∆Н⁰_сг(С₂Н₅ОН) = -1370 кДж/моль.

Значения стандартных энтальпий образования и сгорания сложного вещества зависят от природы вещества и его агрегатного состояния. Числовые значения стандартных энтальпий образования (сгорания) веществ приводятся в справочниках.

Изучением тепловых эффектов (энтальпий) химических реакций и фазовых переходов занимается термохимия.

Энтальпию реакции можно определить как экспериментально, так и методом расчета с использованием стандартных энтальпий образования (сгорания) веществ, участвующих в химической реакции, на основе закона, открытого академиком РАН Г.И. Гессом (1840).

Тепловой эффект реакции, протекающей при постоянном давлении или объеме и при условии, что продукты реакции и исходные вещества имеют одинаковую температуру и отсутствуют другие виды работ, кроме работы расширения, не зависит от пути процесса, а определяется только начальным и конечным состоянием системы.

В термохимических расчетах большое значение имеют следствия из закона Гесса.

Первое следствие.

Тепловой эффект реакции (энтальпия реакции) равен разности между суммой энтальпий образования продуктов реакции и суммой энтальпий образования исходных веществ с учетом их стехиометрических коэффициентов:

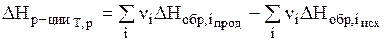. ( 2 )

Это следствие позволяет вычислить энтальпии различных реакций (в том числе и биохимических, осуществление которых in vitro невозможно), используя табличные значения стандартных энтальпий образования продуктов реакции и исходных веществ.

Второе следствие.

Тепловой эффект реакции (энтальпия реакции) равен разности между суммой энтальпий сгорания исходных веществ и суммой энтальпий сгорания продуктов с учетом их стехиометрических коэффициентов:

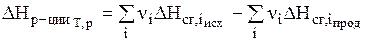. ( 3 )

Третье следствие, известное также как закон Лавуазье – Лапласа.

Тепловой эффект образования соединения из данных веществ равен взятому с обратным знаком тепловому эффекту разложения данного соединения при этих же условиях до тех же исходных веществ.

DН⁰_обр = -DН⁰_cг. ( 4 )

Из закона Гесса также следует, что неизвестная энтальпия реакции может быть получена путем алгебраического суммирования известных энтальпий соответствующим образом подобранных химических реакций.

Первый закон термодинамики и вытекающие из него законы термохимии позволяют составить энергетический баланс термодинамического процесса, но не позволяют сделать заключение о возможности и направлении химического процесса и состоянии равновесия.

Второй закон термодинамики позволяет судить о направлении самопроизвольных процессов и совместно с первым началом устанавливает множество точных количественных соотношений между различными макроскопическими параметрами систем в состоянии термодинамического равновесия.

Процессы, происходящие в определенном направлении без затрат энергии из внешней среды и завершающиеся установлением состояния равновесия, называют самопроизвольными (например, взрыв, коррозия, разряд аккумулятора). Несамопроизвольные процессы (например, заряд аккумулятора) требуют подвода энергии из внешнего источника.

Процессы, протекающие в реальной жизни, являются самопроизвольными и необратимыми. Обратимый процесс (равновесный процесс, который может возвратиться в первоначальное состояние без каких-либо энергетических изменений в окружающей среде или в самой системе под влиянием бесконечно малой силы) является идеализацией.

Во всех необратимых процессах осуществляется более равномерное распределение энергии и вещества, происходит выравнивание в системе температур и других интенсивных параметров. Разупорядоченность, или степень беспорядка системы может быть определена количественно и называется энтропией. Эту функцию ввел Клаузиус и обозначил буквой S. Подобно энтальпии энтропия является экстенсивным свойством системы и функцией состояния системы. Поэтому изменении энтропии в ходе химической реакции может быть найдено в соответствии с первым следствием из закона Гесса: 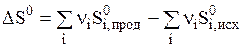. ( 2 )

Формулировки второго начала термодинамики:

- Теплота не может самопроизвольно переходить от более холодного тела к более горячему (Клаузиус).

- Теплота наименее нагретого из тел системы не может служить источником работы, т.е. невозможно превращение только теплоты в работу, тогда как превращение работы в теплоту может быть единственным результатом процесса (Томсон).

- В изолированной системе самопроизвольные (необратимые) процессы происходят в направлении увеличения энтропии системы: dS > 0.

В случае открытых и закрытых систем энтропия не может быть критерием направленности процесс, т.к. кроме изменений в системе, необходимо учитывать изменения в окружающей среде. А это далеко не всегда возможно.

Для таких систем были введены специальные функции состояния, по изменению которых можно судить о направлении самопроизвольного процесса – термодинамические потенциалы.

В зависимости от системы и процесса роль термодинамического потенциала выполняют различные функции:

в изолированной системе (U=const и V=const) – энтропия;

изотермо- изобарный процесс - энергия Гиббса (G);

изотермо- изохорный процесс - энергия Гельмгольца (F);

при S=const и V=const - внутренняя энергия (U);

при S=const и p=const - энтальпия (H).

Термодинамические потенциалы являются критериями направления процесса: в ходе самопроизвольного процесса соответствующий термодинамический потенциал при постоянстве естественных переменных убывает: ∆U_S,V < 0; ∆H_S,p < 0; ∆A_T,V < 0; ∆G_p,T < 0, (энтропия – возрастает ∆S_U,V > 0). При этом потенциал стремится к некоему экстремальному значению: энтропия – к максимуму, все остальные – к минимуму, которому соответствуют равновесное состояние системы. В состоянии равновесия изменения всех потенциалов становиться равным нулю.

Для процессов, происходящих на Земле и в живых организмах, наибольшее значение имеет изотермо-изобарный потенциал – энергия Гиббса. Биохимические реакции, сопровождающиеся уменьшением энергии Гиббса, называются экзэргоническими реакциями, они могут совершаться самопроизвольно. Биохимические реакции, сопровождающиеся увеличением энергии Гиббса, называются эндэргоническими, и они не возможны без внешнего подвода энергии. Например, процесс фотосинтеза в растениях идет только под воздействием солнечной энергии. В живых организмах эндэргонические реакции происходят за счет их сопряжения с экзэргоническими реакциями.

Рассчитать стандартную энергию Гиббса можно по уравнениям:

1) Уравнение изотермы: ∆G⁰ = -RTlnK_p.

2) Следствие из закона Гесса:

∆G⁰₂₉₈ = å(n_i∆G⁰_i)_прод - å(n_i∆G⁰_i)_реаг.

3) Уравнение Гиббса – Гельмгольца: ∆G⁰ = ∆Н⁰ - Т∆S⁰ (при условии, что все составляющие уравнения взяты при одинаковой температуре).

Примеры решения задач

Пример 1.

В результате реакции, термохимическое уравнение которой:

4NO₂ + O₂ = 2N₂O₅ + 109,4 кДж

выделилось 27350 Дж теплоты. Рассчитать массу затраченного кислорода и объем израсходованного оксида азота (IV) (при н.у.).

Решение:

Выделение или поглощение теплоты в ходе реакции происходит в строго эквивалентных количествах, поэтому:

При участии 4 моль NO₂ выделяется 109400 кДж теплоты,

А при участии х моль NO₂ - 27350 кДж теплоты:

Отсюда х равен: х = 4∙27350/109400 = 1 моль.

Объем оксида азота (IV) при н.у. может быть найден по формуле: V = n ∙ V_m.

V(NO₂) = 1 ∙ 22,4 = 22,4 л.

Составим пропорцию для нахождения массы кислорода:

1 моль О₂ – 109400 кДж теплоты;

х моль О₂­ – 27350 кДж теплоты.

Отсюда: х = 1 ∙ 27350 / 109400 = 0,25 моль.

Масса кислорода: m(O₂) = n ∙ M = 0,25 ∙ 32 = 8 г.

Ответ: Масса затраченного кислорода равна 8 г, а объем оксида азота 22,4 л.

Пример 2.

Рассчитать стандартную энтальпию сгорания этанола, если известно, что при сгорании 4,6 г спирта выделяется 137 кДж теплоты.

Решение:

Тепловой эффект реакции (теплота) и энтальпия равны по значению, но притивоположны по знаку, следовательно, энтальпия сгорания 4,6 г спирта составляет -137 кДж.

По определению, стандартная энтальпия сгорания, это энтальпия сгорания 1 моль вещества. Определим, сколько моль составляет 4,6 г спирта:

n = m / M = 4,6 / 46 = 0,1 моль.

Составим пропорцию:

Энтальпия сгорания 0,1 моль составляет -137 кДж;

А энтальпия сгорания 1 моль - х кДж;

Отсюда: х = 1 ∙ (-137) / 0,1 = -1370 кДж.

Ответ: - 1370 кДж/моль.

Пример 3.

При образовании 134 г СО₂ выделилось 787 кДж теплоты. Определить стандартную энтальпию сгорания углерода.

Решение:

Образование углекислого газа и сгорания углерода до высшего оксида – это одна и та же реакция:

С + О₂ = СО₂,

энтальпия которой и является стандартной энтальпией сгорания С и стандартной энтальпией образованияСО₂.

Поэтому определим по имеющимся данным стандартную энтальпию образования СО₂, т.е. энтальпию образования 1 моль СО₂. Учтем, что энтальпия и тепловой эффект реакции равны по величине, но противоположны по знаку.

Рассчитаем количество вещества СО₂: n = m / M = 134 / 44 = 3 моль.

Составим пропорцию:

Энтальпия образования 3 моль СО₂ составляет -787 кДж,

а энтальпия образования 1 моль СО₂ – х кДж;

Отсюда: х = 1 ∙ (-787) / 3 = -262,3 кДж.

Ответ: Энтальпия сгорания С равна - 262,3 кДж/моль.

Пример 4.

Определить тепловой эффект реакции синтеза диэтилового эфира, применяемого в медицине для наркоза, при 298К;

2С₂Н₅ОН(ж) = С₂Н₅ОС₂Н₅(ж) + Н₂О (ж),

если известны стандартные энтальпии сгорания веществ, участвующих в реакции:

ΔН⁰_с (С₂Н₅ОС₂Н₅(ж)) = -2727 кДж/моль;

ΔН⁰_с (С₂Н₅ОН(ж)) = -1371 кДж/моль;

ΔН⁰_с (Н₂О(ж)) = 0 кДж/моль.

Решение:

Используя второе следствие из закона Гесса, получим:

ΔН⁰_r = [2ΔН⁰_с (С₂Н₅ОН(ж))] - [ΔН⁰_с (С₂Н₅ОС₂Н₅(ж)) + ΔН⁰_с (Н₂О(ж))] = [2(-1371)] - [(-2727) + 0] = - 15 кДж/моль.

Ответ: ΔН⁰_r = - 15 кДж/моль – процесс экзотермический.

Пример 5.

Вычислить энергию Гиббса тепловой денатурации трипсина при 50°С, если DН⁰₂₉₈ = 283 кДж/моль, DS⁰₂₉₈ = 288 Дж/моль∙К. Протекает ли эта реакция в данных условиях? Считать, что энтальпия и энтропия в данном интервале температур являются постоянными.

Решение:

Согласно уравнению Гиббса – Гельмгольца: DG⁰_T = DН⁰_T - TDS⁰_T:

DG⁰₃₂₃ = 283 кДж/моль - 323∙288∙10^-3 кДж/моль = 190 кДж/моль.

Ответ: DG⁰₃₂₃ = 190 кДж/моль > 0, реакция самопроизвольно не протекает.