Момент сил относительно точки и оси
Момент силы относительно точки определяется произведением модуля силы на длину перпендикуляра, опущенного из точки на линию действия силы (рисунок 4).
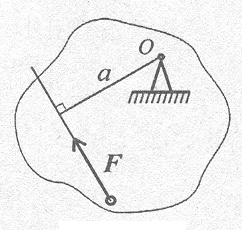
Рисунок 4 – Момент силы F относительно точки О
При закреплении тела в точке О сила F стремится поворачивать его вокруг этой точки. Точка О, относительно которой берется момент, называется центром момента, а длина перпендикуляра а называется плечом силы относительно центра момента.
Момент силы F относительно О определяется произведением силы на плечо.
МО(F) = F·a.
Момент принято считать положительным, если сила стремится вращать тело по часовой стрелке, а отрицательным — против часовой стрелки. Когда линия действия силы проходит через данную точку, момент силы относительно этой точки равен нулю, так как в рассматриваемом случае плечо а = 0 (рисунок 5).
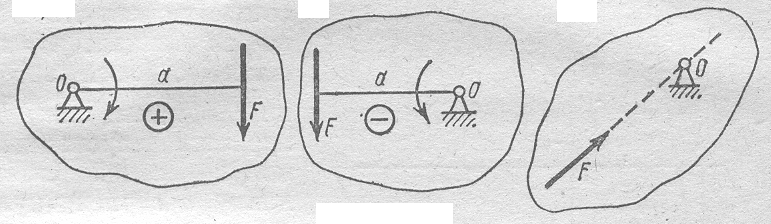
Рисунок 5 – Определение знака момента силы относительно точки
Между моментом пары и моментом силы есть одно существенное различие. Численное значение и направление момента пары сил не зависят от положения этой пары в плоскости. Значение и направление (знак) момента силы зависят от положения точки, относительно которой определяется момент.
Уравнения равновесия плоской системы сил
Условия равновесия сил на плоскости: для равновесия системы сил, произвольно расположенных в плоскости, необходимо и достаточно, чтобы главный вектор и главный момент этих сил относительно любого центра каждый в отдельности равнялся нулю.
FГЛ = 0; МГЛ = Σ МО (Fi) = 0.
Получим основную форму уравнения равновесия:
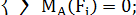
Теоретически уравнений моментов можно записать бесконечное множество, но практически для решения задач на плоскости достаточно трех уравнений равновесия. В каждом конкретном случае используются уравнения с одним неизвестным.
Для разных случаев используются три группы уравнений равновесия:
1. Первая форма уравнений равновесия
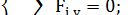
2. Вторая форма уравнений равновесия
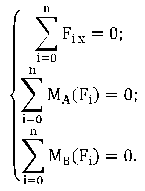
3. Третья форма уравнений равновесия
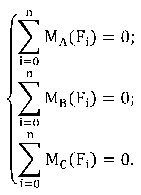
Для системы параллельных сил (рисунок 43), можно составить только два уравнения равновесия:
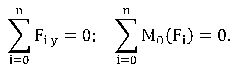
Пример.
Дано: F = 24 кH; q = 6 кН/м; М = 12 кН·м α = 60°; а = 1,8 м; b = 5,2 м; с = 3,0 м. Определить реакции VA, HA и VВ (рисунок 6).
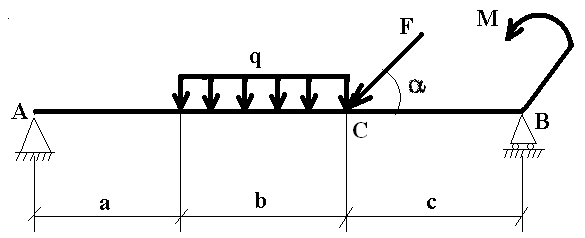
Рисунок 6 – Заданная двухопорная балка
Решение:
Отбрасываем связи (опоры А и В), заменяем их действие реакциями: неподвижная опора имеет реакции VА (вертикальная) и HА (горизонтальная). Подвижная опора — реакцию VB (вертикальная). Выбираем систему координат ХУ с началом в левой опоре, определяем равнодействующую распределенной нагрузки:
Q = q·a2 = 6·5,2 = 31,2 кН.
Чертим расчетную схему балки (рисунок 7).
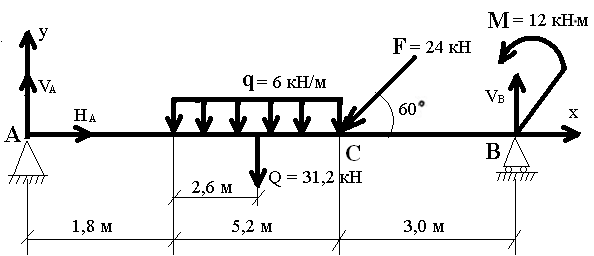
Рисунок 7 – Расчётная схема балки
Для полученной произвольной плоской системы сил составляем уравнения равновесия:
∑Fix = 0; HA – F·cos60° = 0;
∑Fiу = 0; VA – F·cos30° – Q + VB = 0;
∑МА(Fi) = 0; Q·(1,8 + 2,6) + F·cos30°·(1,8 + 5,2) – М – VB·(1,8 + 5,2 + 3) = 0.
Решаем систему уравнений.
HA = F·cos60° = 24·0,5 = 12 кН;
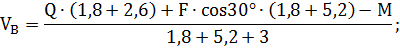
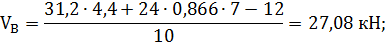
VA = F·cos30° + Q – VB = 24·0,866 + 31,2 – 27,08 = 24,9 кН.
Для проверки правильности решения составим сумму моментов относительно точки приложения наклонной силы F:
∑МА(Fi) = VA·(1,8 + 5,2) – Q·2,6 – М – VB·3 = 24,9·7 – 31,2·2,6 – 12 – 27,08·3 = – 0,06.
Ответ: опорные реакции балки равны VA = 24,9 кН; VВ = 27,08 кН; НА = 12 кН.
Контрольные вопросы:
1. Что определяет эффект действия пары сил?
2. Зависит ли эффект действия пары сил от её положения в плоскости?
3.Зависят ли значения и направление момента силы относительно точки от взаимного расположения этой точки и линии действия силы?
4. Когда момент силы относительно точки равен нулю?
5. Сколь независимых уравнений равновесия можно составить для плоской системы параллельных сил?
