Температура пламени для газовоздушных смесей на нижнем концентрационном пределе распростронения пламени

Горючий газ	Нижний предел воспламенения, об. %	Температура пламени, оС
Метан	5,0
Этан	2,9
Пропан	2,1
Бутан	1,8
Пентан	1,4
Гексан	1,3
Гептан	1,0

Как видно из табл. 4.1, температура пламени при горении различных горючих веществ в воздухе на нижнем концентрационном пределе распростронения пламени – величина практически постоянная.

Установлено также, что на нижнем пределе воспламенения равные объемы смесей большого числа газов и паров выделяют одинаковое количество тепла.

Согласно законам теплового взрыва, достижение НКПР обусловливается равновесием между тепловыделением за счет экзотермичности процесса окисления и теплопотерями из зоны реакции. Так как основным содержанием смеси на НКПР является воздух, то можно полагать, что теплопотери для одних и тех же условий для любых газов будут определяться условиями теплоотвода практически через воздух, т.е. будут одинаковы.

Учитывая указанное выше условие предела теплового взрыва (равновесие между тепловыделением и теплопотерями из зоны реакции), можно полагать, что для рассматриваемых смесей теплотворная способность элемента объема также будет одинакова. А если так, то и тепловой эффект, а значит, и повышение температуры будут на нижнем пределе воспламенения одинаковы для всех горючих паров и газов.

Более строго постоянство температуры горения газовых смесей на нижнем концентрационном пределе распростронения пламени доказано Я.Б. Зельдовичем. Он получил количественное решение задачи определения пределов распространения пламени (пределов воспламенения), согласно которому температура горения на нижнем пределе воспламенения весьма слабо зависит от начальной температуры и состава смеси. Согласно этой теории, появление пределов распространения пламени (концентрационных пределов воспламенения) обусловливается неадиабатичностью процесса горения вследствие теплопотерь в окружающую среду. Наличие этих теплопотерь вызывает необходимость предположения конечных пределов значений скорости распространения пламени. Эти конечные значения определяют концентрационные пределы распространения пламени.

Если скорость пламени с учетом теплопотерь обозначить U, скорость пламени без учета теплопотерь 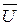и максимальную теоретическую температуру горения T , то соотношение между скоростями пламени при адиабатическом протекании процесса и учете теплопотерь выразится так:

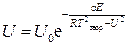, (4.5)

где Е – энергия активации; a – константа.

Я.Б. Зельдович установил, что уравнение (4.5) имеет нетривиальное решение только при

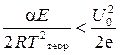. (4.6)

Следовательно, распространение пламени возможно только при условии, если 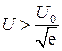или на пределе

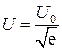. (4.7)

Дальнейшие преобразования приводят к тому, что

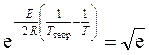, (4.8)

где Т – истинная температура горения. Отсюда

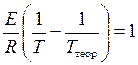(4.9)

или

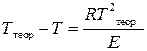. (4.10)

Из уравнения (4.10) следует, что максимальное падение температуры горения на пределе от теоретической составляет:

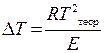. (4.11)

Это условие и есть количественное решение задачи пределов распространения пламени. Если в уравнении (4.11) Т выразить через скорость химической реакции и константы, характеризующие теплоотдачу и т.п., то в результате для температуры горения на пределе получится трансцендентное уравнение. Поскольку в уравнении (4.11) есть экспонента, то решение его приводит к выводу, что температура горения на пределе весьма слабо зависит от начальной температуры и состава смеси, т.е. равные объемы смесей большого числа горючих паров и газов выделяют одинаковое количество тепла.

Теоретические предпосылки были экспериментально подтверждены, что послужило основанием для разработки универсальных приборов, определяющих суммарное содержание горючих газов и паров, модификаций СВК, СТХ, "ЩИТ", СТМ. Сравнительные характеристики современных стационарных термохимических газоанализаторов приведены в табл. 4.2. Схема принудительного забора контролируемой среды на анализ показана на рис. 4.2.

Таблица 4.2