Уравнение Бернулли. Статическое и динамическое давления.

14.

.

Т 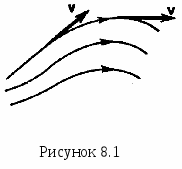ечение жидкости графически изображают линиями тока- воображаемыми линиями, касательные к которым в каждой точке совпадают с направлением вектора скорости частиц, а их густота пропорциональна значению скорости.

Рассмотрим установившееся течение идеальной жидкости.

Установившимся или стационарнымназывается течение, при котором скорости частиц в каждой точке потока со временем не изменяются (при этом условии линии тока совпадают с траекториями частиц жидкости).

В 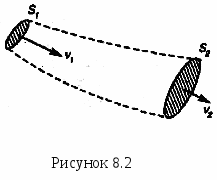ыделяя часть потока, ограниченную линиями тока, получим трубку тока. На рис. 8.1 трубка тока ограничена пунктирными линиями. Сечения трубки тока, напримерS₁иS₂(перпендикулярные скорости), различны, поэтому и скорость в этих сечениях неодинакова.

Условие неразрывности струи предусматривает, что струя жидкости нигде не имеет разрывов. Частицы жидкости при стационарном течении движутся по линиям тока, поэтому боковую поверхность трубки тока жидкость не пересекает.

Если за промежуток времени ∆t в трубку тока вошел объем жидкости V , то такой же объем за такой же промежуток времени ∆t должен выйти из трубки тока.

Выберем малый промежуток времени ∆t и будем считать, что вместе с жидкостью передвигаются сеченияS₁иS₂. Тогда они переместятся на расстояние, соответственно равное ℓ₁= υ₁∆tи ℓ₂= υ₂∆t. Переместившиеся объемы жидкости

V1= υ1∆tS1 иV2= υ2∆tS2

При этом объемы одинаковы, т. е. V₁=V₂, поэтому

υ₁S₁= υ₂S₂ (8.1)

Данное уравнение, выведенное для двух сечений потока несжимаемой жидкости, называется уравнением неразрывности.

В общем случае для идеальной жидкости в стационарных условиях произведение скорости на поперечное сечение трубки тока остается неизменным в любом сечении трубки, т. е. уравнение неразрывности имеет вид

υ S= соnst(8.2)

Из уравнения неразрывности следует, что в более узком сечении трубки тока скорость должна быть больше, чем в более широком сечении (рис. 8.1).

Уравнение Бернулли. Статическое и динамическое давления.

Теорема: вероятность того n независимых событий, в каждом из которых вероятность появления события=р, данное событие наступает К раз в безразлично какой последовательности, равна

Или Р_n(К)=Pⁿ *q^n-k

Это и есть уравнение Бернулли. Все члены уравнения, как легко убедиться, имеют размерность давления и называются: 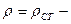статистическим: 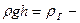гидростатическим: 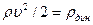- динамическим. Тогда уравнение Бернулли можно сформулировать так:

при стационарном течении идеальной жидкости полное давление равное сумме статического, гидростатического и динамического давлений, остается величиной постоянной в любом поперечном сечении потока.

Для горизонтальной трубки тока гидростатическое давление ос­тается постоянным и должна быть отнесено в правую часть уравнения, ĸᴏᴛᴏᴩᴏᴇ при этом принимает вид

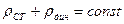
статистическое давление обусловливает потенциальную энергию жидкос­ти (энергию давления), динамическое давление — кинетическую.

Из этого уравнения следует вывод, называемый правилом Бернулли:

статическое давление невязкой жидкости при течении по горизон­тальной трубе возрастает там, где скорость ее уменьшается, и на­оборот.

27.