Схема кинетики внутренних термических напряжений

Стальной стержень

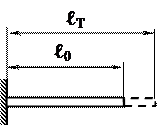При равномерном нагреве на температуру ΔТ закрепленного одним концом стержня с начальной длиной ℓ₀ его длина увеличится и составит

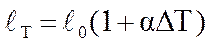
Термическая деформация стержня равна

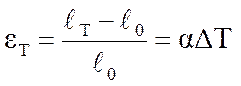
При жестком двухстороннем закреплении стержня его свободная термическая деформация невозможна и в нем возникают термические напряжения сжатия

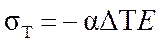
Совместим графики зависимостей предела текучести и термических напряжений в стержне от температуры.

tgβ = –αЕ

Нарастание напряжений в стержне будет идти по прямой ОА, наклоненной к оси Т под углом β (tgβ = –αЕ). Если термические напряжения в стержне не превышают предела текучести (точка А), то стержень при остывания будет разгружаться по прямой АО . При полном остывании стержень вернется в исходное состояние (точка О).

Если термические напряжения достигнут предела текучести в точке В, то при дальнейшем нагреве стержень будет пластически деформироваться, а напряженное состояние в нем будет меняться по пути А-В-С. При остывании от температуры Тс стержень будет упруго разгружаться по прямой СD║AO. Из графика разгрузки следует, что после полного остывания в стержне будут иметь место остаточные растягивающие напряжения (точка D).

Приведенный анализ показывает, что причиной появления растягивающих остаточных напряжений в жестко защемленном стержне является пластическая деформация в процессе нагрева. При ее достаточном уровне (нагружение при нагреве по пути ОBD) уровень растягивающих остаточных напряжений может достичь предела текучести.

При удалении закреплений стержень освободится от остаточных напряжений и деформируется на величину ε = – σ_ост / Е, т.е. укоротится.

Местный нагрев пластины

В процессе воздействия термического цикла сварки сварное соединение нагревается неравномерно. Свободному термическому расширению более нагретых участков препятствует жесткость соседних менее нагретых участков, при этом все участки сварного соединения деформируются совместно.

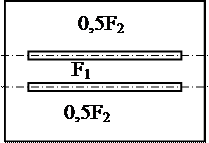
Рассмотрим модель сварного соединения в виде пластины с двумя прорезями, расположенными для простоты анализа симметрично оси Средняя полоса площадью F₁ подвергается нагреву, соседние полосы площадью 0,5F₂ остаются ненагретыми, причем F₁ < F₂ .

При нагреве средней полосы не может свободно деформироваться из-за реакции крайних полос. В средней полосе появляются напряжения сжатия, в крайних – растяжения.

Если бы крайние пластины имели бесконечную жесткость, то в средней полосе упругие напряжения определялись бы аналогично ранее рассмотренному случаю жестко защемленного стержня. С учетом податливости крайних полос упругие термические напряжения во внутренней полосе определятся по формуле, выведенной с учетом равенства нулю внутренних усилий

,

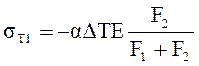При F₂ ® ¥ формула сводится к случаю жестко защемленного стержня.

Реактивные напряжения в крайних полосах равны

.

σs(Т)

О

σs, σТ

Т

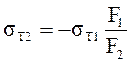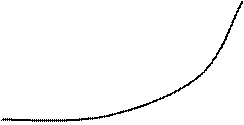
На графике показана схема кинетики внутренних напряжений .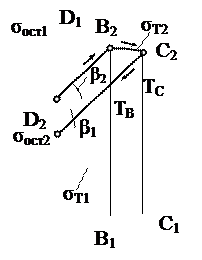

Характер изменения напряженного состояния в средней полосе качественно подобен случаю жестко защемленного стержня – по достижению термических напряжений предела текучести их рост определяется графиком зависимости σ_s(Т). Отличием является величина угла наклона прямых роста упругих напряжений и разгрузки при остывании, определяемого из соотношения

.

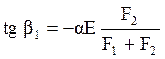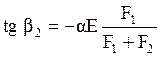
В случае несимметричного расположения прорезей расчетные формулы усложняются, т.к. в пластине появляется изгибающий момент.