Второе начало термодинамики. Энтропия
Прежде чем сформулировать второе начало термодинамики, уточним понятие работа.
Работой называется энергия, передаваемая от одних тел к другим в процессе взаимодействия. Число форм работы так же велико, как велико число форм движения.
Работа равна произведению двух величин – обобщенной силы – I (интенсивный параметр) и обобщенной координаты ξ (экстенсивный параметр)
А = I ξ .
Некоторые формы работы
| Форма работы | Интенсивный параметр | Экстенсивный параметр | Формула |
| Механическое перемещение Механическая деформация Электрическая работа Тепловая работа | Сила F Давление р Потенциал U Температура Т | Путь S Объем V Заряд q Энтропия S | ΔА = F δS ΔА = p δV ΔА = q δU ΔА = T δS |
Применительно к задачам химической термодинамики определяется: физико-химические процессы являются необратимыми, т.е. самопроизвольно развивиаются в сторону выравнивания обобщенных сил ( интенсивных параметров). Момент выравнивания интенсивных параметров соответствует достижению термодинамического равновесия.
Рассмотрим пример.
Если ящик, наполненный сверху черными, а сверху – белыми шарами, встряхивать, то можно добиться полного перемешивания, но невозможно получить разделение шаров по цвету. Дальнейшее встряхивание не приведет к существенному изменению взаимного расположения шаров, т.е. система будет находиться в неизменном макросостоянии или термодинамическом равновесии. Ему в данном примере соответствует наиболее равномерное распределение шаров или наибольшее число способов взаимного расположения.
Применительно к термодинамической системе состоянию равновесия соответствует максимальное число размещений частиц или наибольшего беспорядка. Мерой распределения частиц в фазовом пространстве является энтропия системы. С увеличением степени беспорядка энтропия системы возрастает. Если 1 моль системы в результате обратимого процесса поглотит бесконечно малую порцию теплоты δQ, то приращение энтропии системы составит
dS = δQ/T.
Приближение dS → 0 и S → max указывает на приближение системы к равновесию. Поэтому энтропия является весьма важным в информативном отношении параметром системы.
Для чистых веществ энтропия для чистых веществ при нагреве от 0оК рассчитывается по уравнению
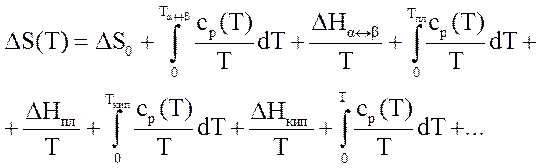
Для смесей и растворов энтропия резко возрастает, т.к. увеличивается число возможных состояний. Для идеальных газов этот прирост учитывается для энтропии i-ого компонента соотношением
Si(T) = S0i (T) – R ln Ni ,
где Ni – молярная концентрация i-ого компонента;
Si(T)– энтропия i-ого компонента в смеси при температуре Т;
S0i (T)– энтропия i-ого компонента в чистом виде;
R – универсальная газовая постоянная.
Если Ni → 0,то энтропия стремится к бесконечности, т.е. выделение вещества из смеси сопряжено со значительными энергетическими затратами.
Для практических расчетов значения энтропии для чистых веществ табулированы для стандартных условий, а также для различных температур.
Энергия Гиббса
Энтропия как термодинамическая функция указывает своим изменением направление самопроизвольно изменяющегося процесса – стремление к равновесию
dS → 0 и S → max при V = const, U = const.
Для большинства физико-химических процессов условие постоянства внутренней энергии неудобно, т.к. она неизбежно меняется.
Большинство металлургических процессов протекает при постоянных давлении и температуре, поэтому более удобна энергия Гиббса или изобарный потенциал
G = H – TS.
Условие стремления к равновесию
dН → 0 и Н → min при T = const, р = const.
Для чистых веществ энергия Гиббса определяется из справочной литературы.
Рассмотрим пример расчета условий равновесия реакции образования углекислого газа
2СО +О2 ↔ 2 СО2.
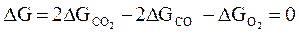 .
.
Однако любая равновесная система представляет собой смесь различных газов, энтропия которых зависит от концентрации
Si = S0i – R ln Ni ,
Тогда энергия Гиббса равна
Gi = Hi - TS0i + RT ln Ni.
Сделаем подстановку
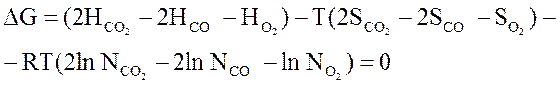 .
.
ΔG = ΔHi - TΔS + RT ln KN =0 ,
.
КN называется константой равновесия реакции и дает возможность определить соотношение молярных долей реагирующих газов в состоянии равновесия. В справочной литературе имеются данные по стандартному изменению энергии Гиббса различных реакций
ΔG0 = – RT ln KN = ΔН – TΔS.
