Примеры решения типовых задач. Пример 1. Как изменится начальная скорость простой реакции образования NOСl2
Пример 1. Как изменится начальная скорость простой реакции образования NOСl2
2NO(г)+ Cl2(г) = 2NOCl2(г),
если уменьшить объем газовой смеси в 2 раза?
Решение. Скорость данной реакции равна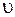 
=k[NO]2[Cl2 ].
Если обозначить концентрации NO и Cl2 до изменения объема, соответственно, через a и b, тогда 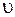=k∙a2∙b.
В результате уменьшения объема в 2 раза концентрации NO и Cl2 увеличиваются в 2 раза, и скорость реакции станет равна
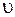*=k(2a)2∙2b=8k∙a2∙b=8 .
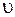Тогда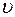 
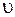*/ =8. Таким образом, скорость реакции увеличится в 8 раз.
Пример 2. Скорость разложениявещества А описывается кинетическим уравнением первого порядка. Определите концентрацию вещества А через 100 с после начала реакции, если известно, что начальная концентрация его составляла 0,01 моль/л, а константа скорости равна 0,023 с-1.
Решение. Используя интегральное кинетическое уравнение реакции первого порядка, имеем
ln[A]t = ln[A]0 – kt;
ln[A]t = ln0,01 – 0,023 ×100;
ln[A]t = – 6,9; [A]t =0,001 моль/л.
Пример 3. Определите энергию активации Еа реакции, для которой при повышении температуры от 22 до 32°C константа скорости возрастает в 2 раза.
Решение. Запишем уравнение Аррениуса для двух температур в виде
,
.
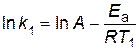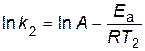В результате вычитания первого уравнения из второго, получим
.
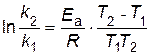Следовательно:
.
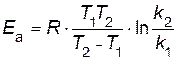Отношение k2 /k1=2 по условию. Переводим температуру в Кельвины и подставляем значения в уравнение
.
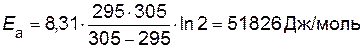Пример 4. Энергия активации некоторой реакции при отсутствии катализатора равна 75 кДж/моль, а с катализатором 50 кДж/моль. Во сколько раз возрастет скорость реакции в присутствии катализатора, если реакция протекает при 25°C?
Решение. Обозначим энергию активации реакции без катализатора через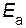 
, а с катализатором – через 
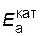; соответствующие константы скорости реакции обозначим через 
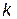и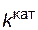 
. Предположим, что величина А для данной реакции постоянна и не зависит от присутствия катализатора. Используя уравнение Аррениуса, находим
,
.
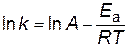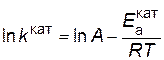В результате вычитания первого уравнения из второго
.
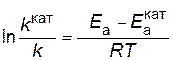Подставляя в последнее уравнение данные задачи, выражая энергию активации в Джоулях и учитывая, что Т=298К, получим
.
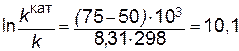
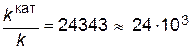Таким образом, в присутствии катализатора скорость реакции возрастет в 24 тысячи раз.
Пример 5. Константа равновесия реакции А+В«C+D равна единице. Исходные концентрации: [А]0=0,01моль/л, [В]0=0,03 моль/л. Определите равновесные концентрации всех четырех веществ.
Решение.
1. Из уравнения реакции видно, что из каждого моля А и В образуется по одному молю С и D. Принимаем, что в ходе реакции к моменту достижения равновесия прореагировало x моль/л вещества А. Если прореагирует х молей А, то должно прореагировать также х молей В, в то же время должно образоваться по х молей С и D.
2. Определяем равновесные концентрации веществ. При протекании реакции в прямом направлении до состояния равновесия происходит уменьшение концентраций исходных веществ и увеличение концентраций продуктов реакции. Поэтому концентрации веществ при равновесии будут:
[A]=0,01 –x, [B]=0,03 –x, [C]=[D]=x.
3. Запишем выражение закона действующих масс. Подставляем в него найденные значения равновесных концентраций.
.
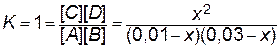4. Решаем уравнение. При этом учитываем, что отрицательный корень не имеет физического смысла и убыль концентрации исходного вещества не может быть больше величины самой концентрации: х=0,0075 моль/л.
5. Находим равновесные концентрации.
[А]=[А]0–x=0,01–0,0075=0,0025 моль/л;
[B]=[B]0–x=0,03–0,0075=0,0225 моль/л;
[C]=x=0,0075 моль/л;
[D]=x=0,0075 моль/л.
Пример 6. В системе А(г)+В(г)«2С(г) равновесные концентрации равны: [А]=0,018 моль/л, [В]=0,011 моль/л, [С]=0,016 моль/л. Определите константу равновесия реакции и исходные концентрации веществ А и В.
Решение. Константа равновесия данной реакции выражается уравнением:
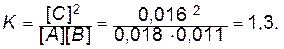
Для нахождения исходных концентраций веществ А и В учтем, что, согласно уравнению реакции, из 1 моля А и 1 моля В образуется 2 моля С. Поскольку по условию задачи в каждом литре системы образовывалось 0,016 моля вещества С, то при этом было израсходовано 0,008 моля вещества А и 0,008 моля вещества В.
Таким образом, исходные концентрации равны:
[А]0 =0,018+0,008=0,026 моль/л;
[В]0=0,011+0,008=0,019 моль/л.
Пример 7. Эндотермическая реакция разложения пентахлорида фосфора протекает по уравнению
PCl5 (г) « PCl3 (г) + Cl2 (г); DН=+92,59 кДж.
Как надо изменить: а) температуру; б) давление; в) концентрации реагирующих веществ, чтобы сместить равновесие в сторону прямой реакции – разложения PCl5?
Решение. В соответствии с принципом Ле Шателье, если на систему, находящуюся в состоянии равновесия, оказать внешнее воздействие, то смещение равновесия происходит в сторону той реакции (прямой или обратной), которая ослабляет эффект внешнего воздействия.
1. Смещение равновесия при изменении температуры связано с тепловым эффектом реакции. Так как рассматриваемая реакция эндотермическая (DНо>0), то для смещения равновесия в сторону прямой реакции нужно повысить температуру.
2. Так как в данной реакции разложение PCl5 ведет к увеличению объёма (из одного моля газа образуются два), то для смещения равновесия в сторону прямой реакции надо уменьшить давление.
3. Чтобы сместить равновесие в сторону прямой реакции, необходимо увеличить концентрацию PCl5.
5. РАСТВОРЫ
Растворами называются гомогенные (однородные) системы, состоящие из двух или более компонентов, относительные количества которых могут изменяться.
Наиболее распространенный вид растворов – жидкие растворы. Любой раствор состоит из растворенного вещества и растворителя, т.е. среды, в которой это вещество равномерно распределено в виде молекул или ионов. Обычно растворителем считают тот компонент, который в чистом виде существует в таком же агрегатном состоянии, что и полученный раствор. Например, в случае водного раствора соли растворитель – вода, а растворенное вещество – соль. Если оба компонента до растворения находились в одинаковом агрегатном состоянии, то растворителем считается компонент, находящийся в большем количестве (пример – смесь воды и спирта).
Растворы занимают промежуточное положение между механическими смесями и химическими соединениями.
Непостоянство состава раствора приближает их к механическим смесям, однако от последних они отличаются своей однородностью.
Отличие растворов от чистых веществ состоит в том, что индивидуальные вещества имеют определенные физические константы, например, температуры плавления и кипения, определенный химический состав, в то время как физические константы и состав растворов зависят от соотношения их компонентов. Например, плотность раствора соли в воде растет, а температура замерзания понижается с увеличением содержания соли. Чистые вещества при изменении их агрегатного состояния не изменяют своего химического состава, а при возвращении в исходное агрегатное состояние приобретают исходные характеристики.
Согласно гидратной теории Д.И. Менделеева, при образовании раствора частицы растворенного вещества вступают во взаимодействие с молекулами растворителя, образуя малоустойчивые соединения, называемые сольватами (или гидратами в случае водных растворов). В зависимости от природы растворенного вещества гидраты образуются за счет ион-дипольного взаимодействия (растворы веществ с ионной структурой, например, солей и полярных молекул; например, HCl) и диполь-дипольного взаимодействия (растворы веществ с молекулярной структурой, например, спиртов).
Идеальным называют раствор, в котором не происходят химические реакции между компонентами, а силы межмолекулярного взаимодействия между компонентами одинаковы. Соответственно образование этих растворов не сопровождается тепловым эффектом (ΔН=0) и каждый компонент ведет себя в растворе независимо от других компонентов. К идеальным растворам по своим свойствам приближаются лишь очень разбавленные растворы, т.е. растворы с очень низкой концентрацией растворенного вещества.