Жұмысты орындау реті. § параметрлерді идентификациялау;
Негізгі
§ параметрлерді идентификациялау;
§ басқару объектілерді модельдеу;
§ нәтижелердің адекваттылығы.
Теориялық негіздері
Бірнеше кірісі және жалғыз шығысы бар объект бар болсын:
 |
Сурет 1.1 – Объекттің құрылымдық сұлбасы
Бұл объекттің статикасын зерттеу барысында тәжірибеші басқа кіріс айнымалылардың мәндерін тұрақты етіп үстап, уақыттың белгілі бір аралығы сайын Xi кіріс айнымалының мәнін ΔXi өсіріп тұруы қажет. Яғни, Xi мәні ретімен Ximin ден Ximax ға өзгереді. Бұл кезде шығыс Y айнымалының мәні тіркеліп тұрады. Тәжірибенің нәтижесінде Х-тің түрлі мәндері мен Y мәні арасындағы сәйкестік кестесі түріндегі статикалық сипаттама пайда болады.
Тәжірибені өңдеу мақсаты – кестелік түрде пайда болған заңдылықты бір аналитикалық F(x) өрнекпен аппроксимациялау.
Жақындастыру (приближение) әдісі үшін тәуелсіз Xi айнымалының бұкіл өзгеру аралығындағы F(X)-Y(X) арасындағы айырмашылықты сипаттайтын бір функционалды минимизациялау тәң. Тәжірибеде квадраттық жақындастыру жиі пайдаланылады. Ол кезде минимизацияланатын функционалдың түрі:
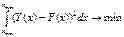 |
Тәжірибелік есептеулерде функционал келесі түрге ие болады:
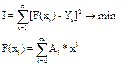 |
(1.1)
Al коэффициенттерін анықтау үшін осы коэффициенттердің әрқайсысы бойынша (1.1)-ді дифференциалдап, пайда болған теңдеулерді нольге теңестіру қажет. Сол кезде біз олардан қажетті коэффициенттерді анықтап алуымызға болатын (m+1) теңдеулер жүйесіне ие боламыз:
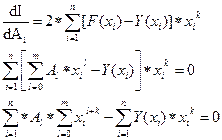 |
k = 0,1,2,...,m
 (1.2) (1.3)
(1.2) (1.3)
Сызықтық түрдегі F(X)=A+B·X функциясы үшін ең кіші квадраттар әдісін қарастырайық.
Пайда болған модельдің адекваттылығын тәжірибенің әр нүктесіндегі орташа салыстырмалы қатені анықтау арқылы тексеруге болады:
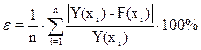 |
(1.4)
бұл жерде: Y(Xi) – тәжірибелік нүктелер
F(Xi) – модель бойынша табылған мәндер
Егер ε 3-5% төмен болса, онда модель тәжірибелік деректерді адекватты сипаттайды деп тұжырымдауға болады.
Білім берудің және оқытудың әдістері:Бақылау сұрақтар мен жүргізілген жұмыс туралы әзірленген есеп бойынша ауызша сұрау.Жұмысты өзіндік орындау
Жұмысты орындау реті
1. ЛАБ1 бағдарламасын іске қосып, сынақ кітапшаңыздың нөмірі бойынша тіркеліңіз.
2. Сол бойынша статикалық сипат алынатын арнаны (Y= f(T), Y= f(Q) не Y = f(F)) таңдаңыз.
3. Кіріс айнымалының өзгертілу аралығын 10-15 бірдей бөліктерге бөліңіз.
4. Кіріс айнымалыны ең кіші мәнінен ең үлкеніне дейін ретімен өзгертіп, шығыс Y айнымалының мәнін тіркеңіз.
5. Қолмен немесе MsExcel не Mathcad жүйелерін пайдаланып қажетті барлық есептеулерді орындаңыз.
6. Осы сияқты әдіспен басқа кіріс айнымалылар үшін бір қатар тәжірибелер өткізіңіз.
7. Қолмен немесе MsExcel не Mathcad жүйелерін пайдаланып қажетті барлық есептеулерді орындаңыз.
8. Оқытушы ұсынған жұмысты орындау бақылау мысалды қолданыңыз.
Әдебиет:
негізгі:
1. Ахназарова С.Л., Кафаров В.В. Методы оптимизации эксперимента в химической технологии: Учебное пособие для вузов. - 2-е изд., перераб. и дополненное. -М.: Высшая школа, 1985. -327с.
2. Инков А.М. Моделирование и идентификация объектов управления. Методические указания к выполнению лабораторных работ для студентов спец. 050702. Шымкент, ЮКГУ, 2010 г., -78 с.
қосымша:
3. Практикум по автоматике и системам управления производственными процессами: учеб. пособие для вузов /под ред. И.М.Масленникова. -М.: Химия, 1986. -336с.
4. Построение математических моделей химико-технологических процессов. Под ред. Дудникова Е.Г. - Л.: Химия, 1970. –312 с.
5. Райбман Н.С., Чадеев В.М. Построение моделей производства. - М.: Энергия, 1975.
Бақылау (сұрақтар, тесттер, тапсырмалар және т.б.)
1) Математикалық модельдерді құрудың регулярлық әдістерінің статистикалық әдістерінен айырмашылығы неде?
2) Статикалық сипаттама дегеніміз не?
3) Объектінің статикалық сипатының динамикалық сипатынан айырмашылығы неде?
4) Статикалық сипатты алу тәжірибені жұргізу әдістемесі.
5) Статикалық сипаттама қандай түрде бейнеленілуі мүмкін?
6) Тәжірибелік деректерді аппроксимациялау әдістері. Олардың жетістіктері мен кемшіліктері.
7) Интерполяциялау әдісі.
8) Квадраттық жақындату (приближения) әдісі.
9) Аппроксимациялаушы тәуелділіктерді сызықтау (линеаризация).
10) Аппроксимациялау нәтижесінде пайда болған математикалық модельдердің адекваттылығын тексеру.
Тақырыб 2:Регрессиялық модельдің параметрлерін анықтау. Басқару объектінің бірфакторлы дисперсиялық анализі
Мақсаты: Жұмыстың мақсаты тәжірибелердің әр нақты сериясы үшін математикалық күтімдердің тең болуы жөніндегі гипотезаны тексеру болып табылады. Студент «Регрессиялық модельдің параметрлерін анықтау. Басқару объектіні бірфакторлы дисперсиялық талдау» тақырыбын оқу барысында алған білімдерін пайдалана білуі керек.
Оқыту мақсаты:
Студент білуге тиіс:
§ математикалық күтімдердің тең болуы жөніндегі гипотезаны;
§ бірфакторлы дисперсиялық талдауы.
Студент істей алуға тиіс:
§ математикалық күтімдердің тең болуы гипотезасын тексеру;
§ Регрессиялық модельдің параметрлерін анықтау.
Тақырыптың негізгі сұрақтары:
Базалық
§ математикалық күтім;
§ дисперсия;
§ Фишер критерий.
Негізгі
§ математикалық күтімдердің тең болуы жөніндегі гипотезасы;
§ есепетеу нәтижелерін сұлба ретінде ұсыну.
Теориялық негіздері
Кез-келген экспериментте бақыланатын шамалардың орташа мәні эксперименттің шарттарын анықтайтын кіріс факторлардың өзгеруіне және кездейсоқ факторларға (сыртқы әсерлерге) байланысты өзгеріп турады.
Дисперсиялық талдаудың мәселесі - орташа мәндердің өзгеруіне факторлардың тигізетін әсерлерін зерттеу.
Дисперсиялық талдау – зерттелетін кездейсоқ шаманың өзгеруіне әкелетін жеке факторларды ерекшелеп, бағалау. Ол үшін қосындылған таңдамалы дисперсияны тәуелсіз факторлар себеп болатын құрамдастарға (составляющие) жіктейді (разложение).
Берілген фактордың әсері маңызды екендігін анықтау үшін кездейсоқ факторларлар себеп болатын ұдайы өңдірілу дисперсиясына сәйкес таңдамалы дисперсияның маңыздығын бағалау қажет.
Эксперименттің нәтижесі n түрлі мәндерді қабылдайтын (n-тәжірибелер серияларының саны) жеке бір А факторына тәуелді болсын. Тәжірибелердің әр сериясы үшін қайталанатын m бақылау жүргізіледі, олардың нәтижелерін келесі түрде жазуға болады:
Y11 Y12 Y13 ... Y1m
Y21 Y22 Y23 ... Y2m
Y31 Y32 Y33 ... Y3m
... ... ... ... ...
Yn1 Yn2 Yn3 ... Ynm
Алынған статистикалық деректердің негізінде нақты әр серия үшін математикалық күтімдердің тең болуы жөніндегі гипотезаны тексеру керек. Егер тексерілетін гипотеза дұрыс болса, онда барлық сериялар үшін орташа арифметикалық мәндердің бір бірінен айырмашылығы жоқ, керісінше жағдайда жобаланған гипотезаны қабылдамау керек.
 - тәжірибелердің i-ші сериясының орташа мәнін, ал
- тәжірибелердің i-ші сериясының орташа мәнін, ал 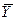 арқылы барлық бақылаулар үшін орта мәнді белгілейік:
арқылы барлық бақылаулар үшін орта мәнді белгілейік:
 |
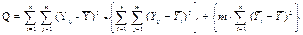 (2.1) (2.1) |
Дисперсиялық талдаудың мағынасы – жеке Yij –дің жалпы орташадан ауытқулары квадраттарының қосындысын екі қосындыға жіктеуде:
Q - әр тәжірибенің (Yij) мәнінің орташадан жалпы ауытқуын анықтайды;
QА - А факторының себебінен пайда болған шашырауды (рассеяние) сипаттайды (екінші фигуралық жақшалардағы өрнек);
Qқалд - кездейсоқ бөгеулер себебінен пайда болған шашырауды сипаттайды (бірінші фигуралық жақшалардағы).
Ауытқулардың квадраттар қосындыларын сәйкесінше еркіндік дәрежелеріне бөліп, келесі дисперсияларды аламыз:
σ2 = Q/f
σА2= QA/f1 (2.2)
σқалд2 = Qқалд/f2
Еркіндік дәрежелер саны: f = m·n -1 f1 = n - 1 f2 = n·(m-1)
Дисперсиялық талдауды орындау - σА2 және σқалд2 бағаларын салыстыруда. Егер әр серия үшін математикалық күтімдер бір біріне тең жөніндегі гипотеза дұрыс болса, онда σ А2 σқалд2 –тан көп аспауы тиіс, ол Фишер критериі бойынша тексеріледі:
F = σА2/ σқалд2 (2.3)
Егер F < Fкр, онда σА2 мен σқалд2 арасындағы айырмашылықты маңызсыз деп санауға болады, демек А факторының әсері кездейсоқ бөгеулер әсерімен шамалас.
Егер F > Fкр, онда σА2 мен σқалд2 арасындағы айырмашылық маңызды, демек А факторы шығыс шамаға әсер тигізеді.
Fкр мәндерін маңыздылықтың α ("альфа") деңгейінде және f1 мен f2 еркіндік дәрежелерінде Фишер таралуының квантильдері бойынша анықтайды:
Fкр = f( α , f1, f2)
Білім берудің және оқытудың әдістері:Бақылау сұрақтар мен жүргізілген жұмыс туралы әзірленген есеп бойынша ауызша сұрау.Жұмысты өзіндік орындау
