А. Ошибки прямых измерений.
Оценку точности и правильности физико-химических измерений производят с помощью следующих характеристик.
1. Среднее арифметическое значение случайной величины 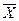 . Пусть X1, Х2,..., Хn обозначают n результатов измерений величины, истинное значение которой Хист. Предполагается, что все измерения проведены одним методом и с одинаковой тщательностью. Такие измерения называют равноточными.
. Пусть X1, Х2,..., Хn обозначают n результатов измерений величины, истинное значение которой Хист. Предполагается, что все измерения проведены одним методом и с одинаковой тщательностью. Такие измерения называют равноточными.
Согласно статистической теории погрешностей при условии выполнения нормального закона (закона распределения Гаусса) среднее арифметическое из результатов измерений является наиболее вероятным значением измеряемой величины ( 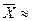 Хист):
Хист):
 (3)
(3)
2. Единичное отклонение εi — отклонение отдельного измерения от среднего арифметического:
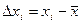 (4)
(4)
Алгебраическая сумма единичных отклонений равна нулю:
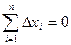
3. Приближенное значение дисперсии 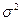 , обозначаемое S2 — это рассеяние случайной величины относительно среднего значения.
, обозначаемое S2 — это рассеяние случайной величины относительно среднего значения.
Для n найденных значений случайной величины:
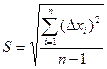 (5)
(5)
4. Приближенное значение средней квадратичной погрешности S равно корню квадратному из приближенного значения дисперсии:
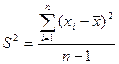 (6)
(6)
5. Относительная квадратичная погрешность, выраженная в % (коэффициент вариации), — отношение приближенного значения средней квадратичной погрешности к среднему арифметическому, умноженное на 100%:
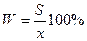 (7)
(7)
6. Приближенное значение средней квадратичной погрешности среднего арифметического:
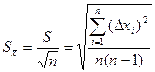 (8)
(8)
- Абсолютная погрешность среднего арифметического
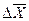 , вычисленная по результатам n независимых (параллельных) определений с использованием коэффициента Стьюдента в предположении, что распределение случайной величины нормальное:
, вычисленная по результатам n независимых (параллельных) определений с использованием коэффициента Стьюдента в предположении, что распределение случайной величины нормальное:
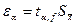 (9)
(9)
где α — доверительная вероятность или надежность; f — число степеней свободы (f = n—1); ta,f — коэффициент нормированных отклонений (коэффициент Стьюдента), который зависит от n и α.
Коэффициент ta, с надежностью α показывает, во сколько раз разность между истинным и средним результатами больше стандартного отклонения среднего результата.
8. Относительная погрешность
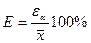 (10)
(10)
9. Доверительный интервал. Согласно формуле (9), интервальные значения измеряемой величины при выбранном коэффициенте надежности ta определяются выражением:
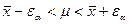 (11)
(11)
из которого следует, что величина доверительного интервала зависит от размера выборки. С уменьшением числа измерений п увеличивается доверительный интервал.
10. Обнаружение промахов. Если Xi - 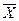 >2S, то результат Xi считают ошибочным (промахом) и при расчете Sx его отбрасывают.
>2S, то результат Xi считают ошибочным (промахом) и при расчете Sx его отбрасывают.
Задание
При потенциометрическом определении рН раствора были получены следующие значения: 4,05; 4,01; 4,03; 4,02; 4,05. Число определений n=5. Требуется определить характеристики точности измерения. (t0,95,4 = 2,776).
Б. Погрешности косвенных измерений.
Косвенным называют такое измерение, при котором вначале проводят прямые измерения некоторых величин (Х1, X2,...), а затем по формулам, связывающим эти величины с измеряемой величиной у, вычисляют ее значение. Наиболее часто вычисление результатов косвенных измерений и их ошибок производят по уравнениям:
| Расчетная формула | Формула для расчета ошибки косвенного определения |
| y = x1 + x2 | 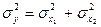 (12) (12) |
| y = x1 – x2 | |
| y = x1 x2 | 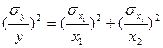 (13) (13) |
| y = x 1 / x2 |
Формулы (12) и (13) показывают, что ошибка анализа, подсчитываемая из приближенного значения дисперсии 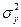 , определяется суммой соответствующих дисперсий; при суммах или разностях измеряемых величин складываются дисперсии абсолютных ошибок (12), при произведениях или частных измеряемых величин складываются дисперсии относительных ошибок (13).
, определяется суммой соответствующих дисперсий; при суммах или разностях измеряемых величин складываются дисперсии абсолютных ошибок (12), при произведениях или частных измеряемых величин складываются дисперсии относительных ошибок (13).
Пример. Вычислить относительную погрешность определения теплоемкости калориметрической системы (С), рассчитываемой по формуле
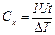
по опытным данным: сила тока I=1,12 А; напряжение U = 6,15 В, время t =200,5 с; найденное изменение температуры системы ΔТ=0,800°. Цена деления амперметра 0,02 А, вольтметра 0,05 4В, термометра Бекмана 0,01°, секундомера 0,2 с.
Решение. Согласно опытным данным: 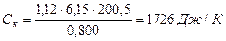
Погрешности измерения величин на приборах часто принимают равными половине цены деления шкалы. Если какая-либо величина представляет собой разность двух измерений, например ΔТ, то погрешность определения ΔТ' удваивают. Допустим, что Δ I =±0,01 A; ΔU= ±0,025 В; Δt = ± 0,1 с; ΔТ'=±0,005° Согласно формуле (13):
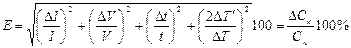
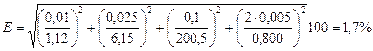
Абсолютная ошибка: 1726·1,7/100 = 29,3 Дж/К. Теплоемкость калориметрической системы С = 1726±29 Дж/К.
Запись результатов измерений. Цифра окончательного результата должна заканчиваться разрядом единиц, которым начинается погрешность. При выполнении работы экспериментатор должен оценить точность отсчета на приборах и в записи результатов не давать лишних цифр. Например, при пользовании термометром со шкалой, разделенной на 0,01°, в лучшем случае можно сделать отсчет с точностью 0,002°. Поэтому неверно выглядела бы запись «4,3724°».
Чтобы конечный результат отвечал заданной точности, необходимо все величины в расчетной формуле определять с точностью на порядок большей.
