Отыскание логарифма по числу

Логарифма целых степеней числа 10 отыскиваются без таблиц. Для отыскания логарифмов остальных чисел поступаем так:

а) Отыскание характеристики. Для чисел, больших единицы, характеристика равна на единицу уменьшенному числу цифр целой части.

Примеры: lg35,28=1,…; lg3,528=0,…; lg60 100=4,…

(точки после запятой означают, что здесь должны стоять цифры мантиссы.)

Для чисел, меньших единицы, характеристика искусственной формы логарифма равна числу нулей перед значащими цифрами числа (считая и нуль целых).

Примеры: lg 0,00635=3,…; lg0,1002=1,…; lg0,06004=2,…

б) Отыскание мантиссы. При отыскании мантиссы десятичной дроби, правильной или неправильной, отбрасываем запятую и ищем в таблице мантиссу получившегося целого числа можно отбросить все нули в конце его (если таковые имеются). Например, мантисса числа 20,73 равна мантиссе числа 2073; мантисса числа 6 004 800 равна мантиссе числа 60 048.

При пользовании четырехзначными таблицами логарифмов у полученного целого числа оставляем только четыре первых знака; при пользовании пятизначными таблицами – первые пять. Остальные отбрасываются, так как они не повлияют (или почти не повлияют) на содержащиеся в таблице разряды мантиссы.

По четырехзначной таблице можно найти непосредственно мантиссу трехзначного числа; по пятизначной – мантиссу четырехзначного числа. Мантиссы четырехзначных (пятизначных) чисел являются прибавлением поправки (см. ниже приводимые примеры).

Четырехзначная таблица

Пример 1. Найти логарифм числа 45,8. Находим (без таблицы) характеристику: 1,…Отбрасывая запятую, имеем целое число N = 458. Берем первые две его цифры (45). В строке 45 отыскиваем число, стоящее в столбе 8. Находим 6609. Это – мантисса. Имеет lg45,8 = 1,6609.

Пример 2. Найти lg 0,02647. Находим (без таблицы) характеристику: 2,… Отбрасываем запятую. Получаем число 2647. Берем первые его две цифры (26); в строке 26 отыскиваем число, стоящее в столбце 4 (третья цифра данного числа). Находим 4216. Это – мантисса lg264. Находим поправку, соответствующую последней цифре 7 данного числа. Она помещается в той же строке 26, в столбце 7 раздела «поправки». Находим 11. Прибавляем поправку к ранее найденной мантиссе. Получаем 4216 +11=4227. Это мантисса данного числа. Имеем lg 0,02647=2,4227.

Запись:

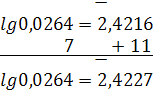
Замечание. Поправки рассчитаны с помощью интерполяции, применение интерполяции облегчает работу вычисления. Из таблицы видно, что мантисса числа 2640 меньше мантиссы числа 2650 на 4232 – 4216 = 16 (десятичных долей). Разности чисел 10 отвечает разность мантисс 16. Порцинальный расчет дает: х:16=7:10=0,7; х=16·0,7=11.

Пятизначная таблица

Пример 1. Найти lg0,02647. Находим без таблиц характеристику lg0,02647=2,… отбрасывая запятую, получаем число 2647. Открываем ту страницу, где есть строки 264. В строке 264 отыскиваем число, стоящее в столбце 7. Находим 275. Это три последние цифры мантиссы. Первые две (42) находим в начале строки. Вся мантисса 42275; lg0,02647 = 2,42275.

Для большинства строк вначале первые две цифры не проставлены. Тогда нужно взять первые две цифры либо из нижней (если перед последними тремя цифрами мантиссы стоит звездочка), либо (если звездочки нет) из ближайшей верхней.

Пример 2. Найти lg 6764. Характеристика есть 3. В строке 676 таблицы логарифмов отыскиваем в столбце 4 три последние цифры мантиссы 020. Они снабжены звездочкой. Поэтому первые две цифры (83) берём из нижележащей строки 677. Вся мантисса 83020; lg 6764 = 3,83020.

Пример 3. Найти lg 6,6094. Находим характеристику: lg 6,6094 = 0,… Отбрасываем запятую, получаем 66094. В строке 660 (соответствующей первым трем цифрам) отыскиваем в столбце 9 (четвертая цифра) число 014 со звездочкой слева. Это последние три цифры мантиссы числа 6609. Первые две (82) находим в следующей строке. Мантисса lg6609 есть 82014. Находим поправку, соответствующую последней цифре 4 данного числа. В столбце РР помещена табличка с надписью 6 (d=6 есть разность между мантиссами чисел 6609 и 6610). В левой части этой таблички отыскиваем число 4. Против него стоит 2,4. Отбрасывая десятые доли, округляем это число до 2. Это поправка. Прибавляя ее ранее найденной мантиссе, получаем 82014 + 2 = 82016. lg 6,6094 = 0,82016.

Запись:

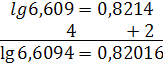
Приложение Б