Основні методи обробки експериментальних даних

19.1. Обробка результатів дослідження

в координатах з рівномірними шкалами

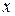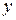Якщо під час нанесення спостережуваних з досліду даних на графік з рівномірними шкалами виявиться, що точки розташовуються поблизу прямої, то залежність змінних, наприклад і , є лінійною функцією. Для подання одержаних даних у вигляді лінійної функції залишається тільки визначити коефіцієнти 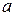і 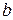у рівнянні:

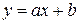. /19.1/

Найбільш зручний і точний спосіб визначення цих коефіцієнтів – спосіб найменших квадратів. Менш точними, але простішими способами визначення коефіцієнтів рівняння прямої лінії, є способи натягнутої нитки і середньої.

19.1.1. Спосіб натягнутої нитки. Ґрунтується на геометричному добиранні прямої візуально. Після нанесення досліджуваних параметрів на графік, який звичайно виконують на міліметрівці, добирають графічну пряму, яка знаходиться найближче до нанесених точок.

Вибравши на цій прямій дві довільні точки, які не обов'язково є спостережуваними значеннями, визначають їхні координати ( 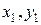), ( )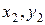. Потім складають рівняння.

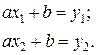/19.2/

Розв’язавши їх, визначають

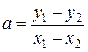. /19.3/

Підставивши значення 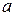в будь-яке з рівнянь, знаходять коефіцієнт .

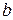19.1.2. Спосіб середньої не потребує графічного зображення експериментальних даних і полягає ось у чому. Нехай маємо якісь експериментальні значення досліджуваних параметрів, наприклад, ( ), ( ),…, ( ).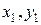

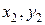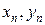Яшо встановлено лінійну залежність 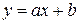, то значення 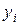будуть відмінні від 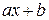внаслідок експериментальних похибок, тобто

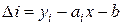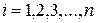( ). /19.4/

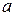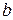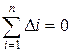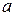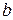Якщо і вибрано так, що для всіх спостережень похибки усереднилися, тобто , то це приведе до одного рівняння. Для знаходження і потрібні два рівняння. У цьому разі чинять так.

Поділяють групу наявних значень на дві частини. Вважають, що усереднення похибок відбувається не тільки для всіх значень, а й для кожної частини окремо.

До першої частини відносять всі значення, які дорівнюють їхньому середньому значенню або менші від нього:

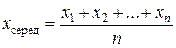. /19.5/

До другої – всі значення параметра, які більші від 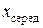. При цьому можна записати два рівняння

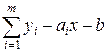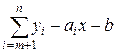, , /19.6/

де 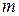– кількість спостережень у першій частині.

Для визначення коефіцієнтів 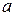і 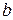одержану систему рівнянь записують у вигляді

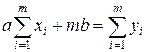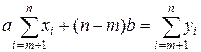; . /19.7/

Якщ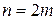о , то

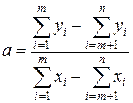. /19.8/

Коефіцієнт 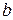визначають за початковими умовами.

19.1.3. Спосіб найменших квадратів дає змогу одержувати більш точні емпіричні формули. При цьому вигляд залежності /прямолінійний чи криволінійний між досліджуваними величинами має бути попередньо знайдений розміщенням експериментальних точок на графіку з рівномірними шкалами. Суть способу найменших квадратів полягає в тому, що сума квадратів відстаней від експериментальних точок до попередньо проведеної лінії є найменшою, тобто

.

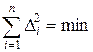Виведення емпіричної формули в цьому разі одержують аналітично.

Якщо між змінними х і у припускається лінійна залежність вигляду 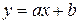, то за експериментальними точками розв’язуванням системи рівнянь масна віднайти значення коефіцієнтів 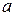і :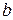

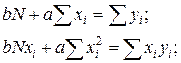, /19.9/

де 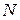– кількість дослідних точок. – кількість дослідник точок.

У практиці дослідних робіт широко застосовують рівняння, які подаються у вигляді степеневих функцій.

Для відшукання способом найменших квадратів коефіцієнта і показника ступеня дану форму треба прологарифмувати, в результаті чого дістають лінійну залежність.

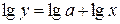. /19.10/

Коефіцієнти 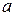і 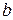визначають розв'язуванням системи рівнянь.

19.2. Обробка результатів дослідження

в координатах з логарифмічними шкалами

У системі координат з рівномірними шкалами всяку непропорціональну залежність зображають кривою лінією. Для відшукання істинної закономірності в цьому разі потрібна велика кількість спостережень. Якщо залежність у разі нанесення одержаних даних на графік з рівномірними шкалами наближається до кривої лінії, тобто має степеневий характер вигляду 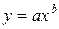, де 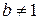, зручніше користуватися системою координат з логарифмічними шкалами.

Прологарифмувавши вираз 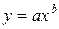, дістають .

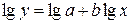Припускаючи, що 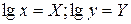, записують рівняння у вигляді

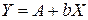. /19.11/

Таким чином, якщо на осях координат відкласти величини 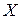і 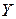, пропорціональн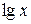і і 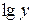, виходить пряма лінія. Отже, в цьому разі всяке рівняння розглядуваного типу зображається в системі координат з логарифмічними шкалами у вигляді прямої лінії, тангенс кута нахилу якої до позитивного напряму осі абсцис дорівнює показнику ступеня 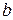. Необхідною умовою побудови графіка в логарифмічних шкалах є рівність масштабів обох осей координат, нормальна до їхнього напряму, і відповідність їхнього початку координат одиниці /0,001; 0,01; 0,1; І; 10 і т.д./. Звичайно такі сітки готують заздалегідь, використовуючи при цьому логарифмічну лінійку. Папір з нанесеною логарифмічною сіткою, який дістав назву логарифмічного, зображено на рис. 19.1.

Пряму в системі координат з логарифмічними шкалами будують описаними способами. Коефіцієнт визначають так само, як і для лінійної залежності, тобто за способом середньої або натягнутої нитки. Тільки в цьому разі координати х і у вимірюють масштабною лінійкою в міліметрах, безпосередньо на логарифмічній сітці, яка повинна мати рівність масштабів обох осей координат. Сталу можна відшукати двома способами: аналітичним і графічним.

Для визначення аналітичним способом треба в рівняння 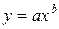підставити відповідно значення 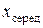і 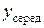для першої і другої груп значень /для першої групи 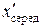= 70 мм, 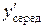= 53 мм; для другої 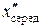= 111 мм, 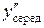= 32 мм і розв’язати його. З двох одержаних значень визначають середнє арифметичне, яке й буде шуканим.

Для визначення сталої а графічним способом подовжують лінію до перетину з віссю координат і на осі ординат одержують її значення

/а = 1,74, див. рис. 19.1/.

19.3. Метод середньоарифметичного знаходження лінії
досліджуваної залежності

Під час нанесення результатів спостережень на графік з рівномірними або з логарифмічними шкалами звичайно виходить розкид точок з обох боків лінії. Дослідження можна визнати якісним і достатнім тільки в разі, якщо точки на графіку з рівномірними шкалами в загальному вигляді розміщуються по певній кривій або по прямій. Якщо цього немає, треба з’ясувати причини розкиду точок і, якщо потрібно, виконати додаткові дослідження.

Метод середньоарифметичного знаходження лінії досліджуваної залежності полягає ось у чому. Нехай маємо дослідні значення ( 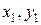), ( ),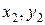..., ( 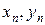). У більшості випадків вони будуть відмінні від 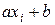через наявність експериментальних похибок. Позначимо через 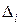відповідну похибку, тоді 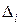= 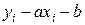, де і = 1,2…, .

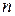Вибравши 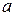і 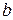так, щоб для всіх спостережень похибки усереднилися, тобто 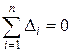, знаходять лінію, яка найбільш точно відображає функціональний зв’язок досліджуваних факторів.

19.4. Визначення кількості значень факторів
і інтервалів між ними

Під час вивчення різних процесів хімічної технології основним завданням є визначення ступеня впливу різних факторів на параметр оптимізації. З метою скорочення дослідної роботи й забезпечення вимог і точності треба вивчити вплив основних факторів за мінімально потрібної кількості їхніх значень. Кількість значень факторів, за яких треба виконати дослідження для побудови графічної залежності й виведення емпіричної формули, залежить від їхніх граничних величин і мас бути тим більша, що більше відношення крайніх величин. Мінімальну кількість їхніх значень, потрібних для виявлення закономірності побудови графічної залежності й виведення емпіричної формули, визначають так:

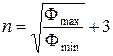/19.12/

де 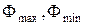– відповідно максимальне й мінімальне числові значення фактора.

Конкретні числові значення фактора, за яких необхідно провести дослідження, встановлюють таким чином.

Якщо досліджувана залежність під час нанесення точок на графік з рівномірними шкалами має прямолінійний характер, то інтервал між двома значеннями визначають за формулою

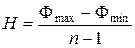. /19.13/

Інтервал у системі координат з логарифмічними шкалами визначають за формулою

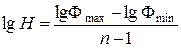. /19.14/

19.5. Визначення залежності від двох
або від кількох змінних факторів

Вивчаючи динаміку процесів, в основному доводиться досліджувати значення кількох факторів. Кінцева мета експериментатора – одержати залежність, яка охоплює всі досліджувані фактори, що впливають на процес, у вигляді

,

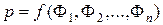де 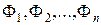– фактори, що впливають на шукану величину.

Таку залежність можна одержати математичною обробкою експериментальних значень способом найменших квадратів.

Цей спосіб більш точний порівняно з іншими, але застосовують його досита рідко. Це пояснюється тим, що в даному разі треба проводити багато експериментів, загальна кількість яких дорівнює добутку числа значень усіх досліджуваних факторів, а також трудомістку обробку результатів спостережень. Тому застосовують інші методи, які значно скорочують об’єм експериментальних і обчислювальних робіт. Найбільш простий з них полягає в наступному.

Вплив кожного фактора на процес досліджують окремо, причому під час проведення такого експерименту всі інші фактори повинні бути постійними й такими, що дорівнюють середньому члену свого ряду. Таким чином, у даному разі проведено дослідження, пов’язані з вивченням впливу на параметр:

першого фактора

,

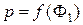коли

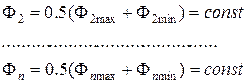/19.15/

другого фактора

,

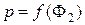коли

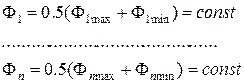. /19.16/

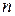-го фактора

,

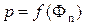коли

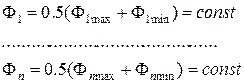. /19.17/

Загальна кількість дослідів 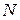у цьому методі дорівнюватиме сумі значень кожного з усіх факторів, які досліджуються, тобто

.

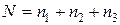За наявними значеннями для кожної з цих залежностей будують графіки в системі координат з рівномірними шкалами. При цьому треба використати для знаходження ліній досліджуваної залежності метод середнього арифметичного, що дає змогу з’ясувати вид функцій /прямолінійна чи криволінійна/.

Потім задача зводиться до визначення показника ступеня для криволінійної функції будь-яким із пропонованих методів. Якщо треба одержати емпіричні залежності від дії кожного фактора окремо, то ці формули можна визначити, застосувавши один з розглянутих способів математичної обробки дослідних значень.

Емпірична залежність параметра від усіх факторів має вигляд

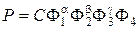, /19.18/

де 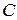– коефіцієнт пропорціональності; 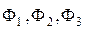– фактори, залежність від яких параметра Р має степеневий характер; 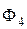– фактор, залежність від якого параметра Р має прямолінійний характер і проходить через початок координат; 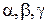– показники ступеня.

Коефіцієнт пропорціональності С визначають підстановкою значень параметра Р і відповідних йому значень факторів, одержаних під час проведення досліду, тобто з відповідних графіків з рівномірною шкалою, лінії досліджуваних залежностей яких проведено з умови, що

.

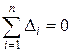Для більшої точності коефіцієнт С визначають як середнє арифметичне даних кількох груп дослідів однієї серії випробувань.