Ориентационная поляризация диэлектрика

Полярный диэлектрик состоит из поляризованных молекул (например, сульфид водорода 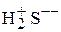), имеющих электрический дипольный момент

,

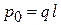где q – модуль заряда иона; l – расстояние между ионами. Диполи разных молекул направлены хаотически по всем направлениям. Внешнее электрическое поле 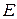поворачивает диполи и устанавливает их вдоль поля, возникает ориентационная поляризация. Тепловое движение разбрасывает направления диполей. Средняя проекция дипольного момента на направление поля определяет степень поляризации диэлектрика. Получимдипольный момент единицы объема.

Количественное описание. В однородном электрическом поле Е, направленном по оси z, потенциальная энергия диполя

.

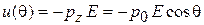Доказательство

Электрическое поле направлено в сторону быстрейшего убывания потенциала. В однородном поле потенциал точки z

.

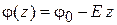Эквипотенциальные поверхности перпендикулярны оси z

.

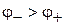Для заряда q потенциальная энергия

,

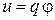тогда энергия диполя

,

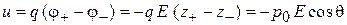где

, .

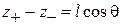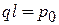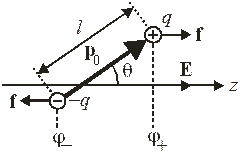
Для получения средней проекции дипольного момента используем распределение Больцмана (2.55)

.

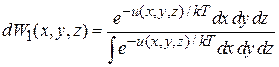Выбираем сферические координаты с осью z, направленной по полю, тогда

.

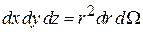Потенциальная энергия 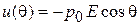не зависит от радиуса. Интегрируем (2.55) по радиусу и получаем

,

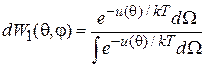где элемент телесного угла

.

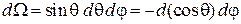Потенциальная энергия не зависят от угла φ. Интегрируем по φ

,

,

.

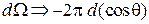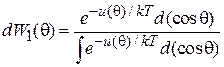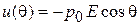Для упрощения вводим

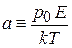– относительная энергия взаимодействия,

,

.

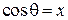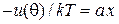Получаем

.

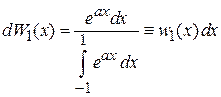Используем

,

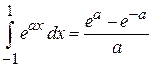находим функцию распределения ориентаций дипольного момента

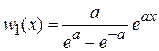. (П.6.7)

Средняя проекция дипольного момента

.

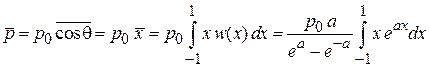Интегрируем по частям

, , ,

.

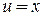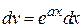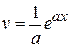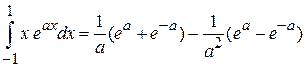Получаем

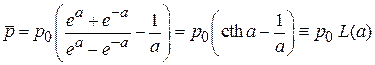, (П.6.8)

где L(a) – функция Ланжевена.

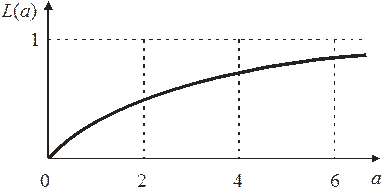
В слабом поле

, ,

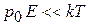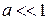разлагаем в ряд

,

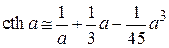получаем

, ,

,

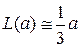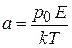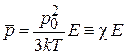где ориентационная поляризуемость

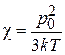
обратно пропорциональна температуре.

В сильном поле

, ,

,

,

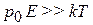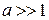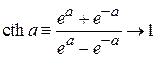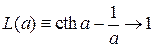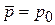
– все диполи ориентированы по полю. Возникает насыщение поляризуемости.

Поль Ланжевен разработал статистическую теорию парамагнетизма в 1905 г. и получил результат, аналогичный (П.6.8).

Петер Дебай применил в 1911 г. статистический метод Ланжевена для поляризации диэлектриков и назвал функцию (П.6.8) именем Ланжевена.

В честь Дебая названа внесистемная единица электрического дипольного момента

1 Д (дебай) = 1×10^–18 ед. СГС = 3,33564×10^–30 Кл×м.

Поль Ланжевен (1872–1946) Петер Дебай (1884–1966)

Термодинамические потенциалы

Основные положения

Статистическая величина характеризует микросостояние, например плотность вероятности.

Термодинамическая величина характеризует макросостояние, и является средним значением статистической величины по микросостояниям фазового ансамбля, например внутренняя энергия. В общем случае термодинамическая величина зависит от текущего состояния системы и от пути перехода в это состояние.

Термодинамический потенциал зависит от состояния системы и не зависит от пути перехода к этому состоянию. Элементарное изменение термодинамического потенциала является полным дифференциалом. Понятие ввел Гиббс в 1874 г.

Примеры. Термодинамические потенциалы отличаются набором своих аргументов – V, T, P, N, S, μ:

· внутренняя энергия ;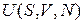

· свободная энергия ;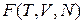

· химический потенциал 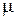может иметь разные аргументы;

· энтропия ;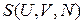

· термодинамический потенциал Гиббса ;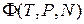

· W-потенциал .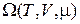

Потенциалами не являются:

· работа A;

· теплота Q.

Соотношения между потенциалами, полученные при постоянном числе частиц N, сохраняются и при переменном N.

Условие равновесия системы. Если система приходит к равновесию в результате некоторого процесса, то в равновесном состоянии минимален тотпотенциал, аргументы которого не изменяются в ходе процесса. Теорема доказывается в термодинамике.

Химический потенциал системы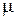

Химический потенциал является энергетической мерой упорядочивающих процессов в системе, в противоположность тепловой энергии, как мере беспорядка. Состояние системы является результатом «конкуренции» между порядком и хаосом.

В систему добавляем частицу, часть термодинамических параметров – 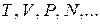меняется. Находим изменение термодинамического потенциала, у которого аргументы, отличающиеся от N, не меняются в процессе добавления частицы. Это изменение равно химическому потенциалу.

При 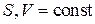получаем

.

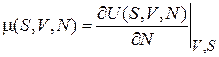Химический потенциал равен изменению внутренней энергии при добавлении частицы, если система сохраняет объем (dV = 0) и не обменивается теплом (dS = 0). Химический потенциал имеет размерность энергии, он равен изменению полной энергии системы при приближении частицы к частицам системы.

Если частицы взаимно притягиваются, то при их сближении сила притяжения совершает работу, расходуя энергию взаимодействия, и она уменьшается. В результате для системы притягивающихся частиц химический потенциал отрицательный.

Если частицы взаимно отталкиваются, то при их сближении внешняя сила совершает работу, увеличивая энергию взаимодействия. В результате для системы отталкивающихся частиц химический потенциал положительный.

Химический потенциал и число частиц системы – взаимно зависимые величины. Химический потенциал находится из условия нормировки на число частиц системы, если это число сохраняется. Если частицы не имеют заряда и их число не сохраняется, то химический потенциал равновесной системы равен нулю.

Электрохимический потенциал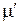

Внешнее потенциальное поле изменяет химический потенциал системы, он получает зависимость от координат и новое название – электрохимический потенциал

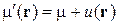, (2.59)

где

m – химический потенциал без внешнего поля;

u(r) – энергия частицы во внешнем поле.

Для частицы с зарядом q в электростатическом поле

,

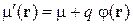где j(r) – потенциал точки поля, где находится частица.

Далее доказывается, что во всех точках равновесной системы электрохимический потенциал одинаковый

,

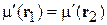поэтому он характеризует не частицу, а систему частиц.

Химический потенциал ввел Гиббс в 1875 г., электрохимический потенциал – Эдвард Арманд Гуггенгейм в 1929 г.

Внутренняя энергия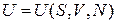

Является средним по фазовому ансамблю значением полной энергии системы

.

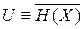Для обратимого процесса при 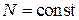первое начало термодинамики дает

.

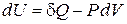С учетом

,

,

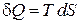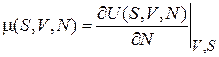при переменном N получаем

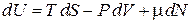. (2.57)

Внутренняя энергия является потенциалом с элементарным приращением в виде полного дифференциала

.

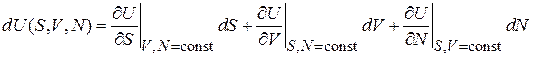Сравнение с (2.57) дает выражения для температуры, давления и химического потенциала через внутреннюю энергию

,

,

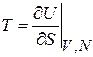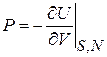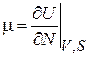. (2.58)

Первые два выражения использовались ранее для систем с постоянным числом частиц.