Открытие электрона и протона

Атомы состоят из мелких частиц, которые были открыты в разное время разными исследователями. Самой первой из таких частиц оказался электрон, несущий единичный электрический заряд.

Электрон получил свое нынешнее название только в самом конце прошлого века, а до этого физики только предполагали, что существует некий "атом электричества", с помощью которого по проводам передается электрический ток.

В 1853 году французский исследователь А. Массон решил попробовать пропускать электрические разряды (искры) через стеклянную трубку, из которой откачан воздух. Впоследствии с помощью этого несложного устройства англичанин Вильям Крукс провел множество опытов, и с тех пор такие трубки называют круксовыми (их прямые "потомки" - редко встречающиеся теперь электронно-лучевые телевизоры и мониторы).

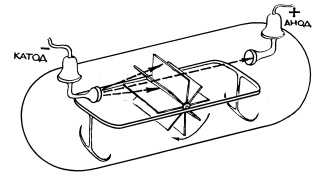
Рисунок 14. 1

Рис. 14.1. Вращение вертушки с лопастями под действием катодных лучей в трубке Крукса. Этот опыт позволял предположить, что катодные лучи больше похожи не на обычный свет, а на поток микроскопических частиц, имеющих массу.

Что же удалось выяснить с помощью круксовых трубок? Они служили источником необычных лучей, которые распространялись отрицательно заряженным электродом - катодом. Эти лучи получили название катодных. Описывая катодные лучи, Крукс отмечал такие их свойства:

- они вызывают свечение некоторых веществ, нанесенных на внутреннюю поверхность трубки;

- они обладают кинетической энергией и способны передавать механическое движение вертушке с лопастями (рис. 14.1);

- они отклоняются магнитным полем;

- они отрицательно заряжены, потому что движутся по направлению к положительному полюсу трубки.

В 1897 году английский физик Дж. Дж. Томсон сконструировал похожую трубку, с помощью которой можно было измерять отклонение катодных лучей в электрическом поле (рис.14.2).

Напряжение, подаваемое на пластины 4 и 5, между которыми проходили катодные лучи, можно было уменьшать или увеличивать. Чем выше было напряжение на пластинах 4 и 5, тем сильнее отклонялся от прямолинейной траектории поток катодных лучей.

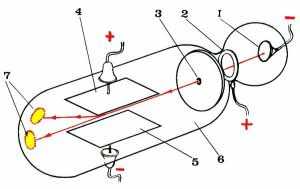
Рисунок 14. 2

Рис. 14.2. Прибор Томсона для измерения отклонения катодных лучей под действием электрического поля. 1 - отрицательно заряженный электрод (катод), 2 - положительно заряженный электрод, 3 - отверстие, 4 и 5 - пластины электродов для отклонения катодных лучей, 6 - часть трубки, покрытая изнутри слоем вещества, светящимся под действием катодных лучей, 7 - светящееся пятно.

Впоследствии этот эксперимент помог установить массу и заряд частиц, из которых состоят катодные лучи: ведь чем меньше масса и чем больше заряд частицы, тем легче отклонить ее от прямолинейной траектории с помощью электрического поля. Правда, для этого потребовались дополнительные эксперименты, но в 1909 году цель была достигнута. Электрический заряд таинственных "катодных" частиц, выраженный в кулонах, оказался величиной чрезвычайно малой, поэтому для удобства физики и химики чаще пользуются другой шкалой, в которой величина этого "элементарного" заряда принята за единицу.

Описанные Томсоном отрицательно заряженные частицы, несущие наименьший электрический заряд, получили название электронов.

Позже в аналогичном приборе удалось наблюдать поток положительно заряженных частиц, которые стали называть протонами. Масса протона оказалась почти в 2000 раз больше массы электрона, а его заряд, как выяснилось, равен заряду электрона, но со знаком "плюс".

Таким образом, в распоряжении физиков появились первые "строительные детали", с помощью которых уже можно было попытаться построить те или иные модели атомов.

Модели атома

Томсон предположил, что атомы состоят из положительно заряженной сферы, в которую вкраплены электроны (рис. 14.3а). Эта модель атома получила среди ученых прозвище "сливовый пудинг", хотя не менее похожа и на булочку с изюмом (где "изюминки" - это электроны), или на "арбуз" с "семечками" - электронами.

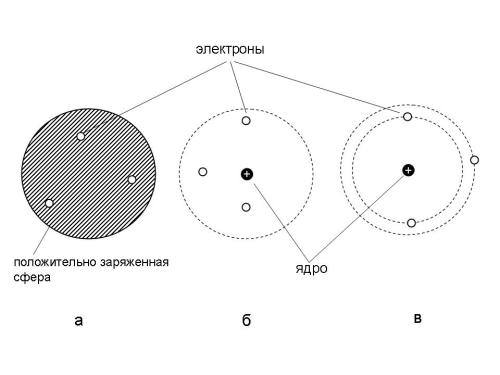
Рисунок 14. 3

Рис. 14.3. Модели атома: а) Томсона (“сливовый пудинг”), б) Резерфорда, в) планетарная модель Бора.

В 1910 году английский физик Эрнст Резерфорд со своими учениками Гейгером и Марсденом провели эксперимент, который дал поразительные результаты, необъяснимые с точки зрения модели Томсона. В то время уже была открыта радиоактивность, о которой в наше время знают даже школьники начальных классов. Радиоактивные вещества способны испускать не только лучи высокой энергии, но и частицы высокой энергии, которые способны проникать сквозь многие предметы. Такие частицы называются альфа-частицами.

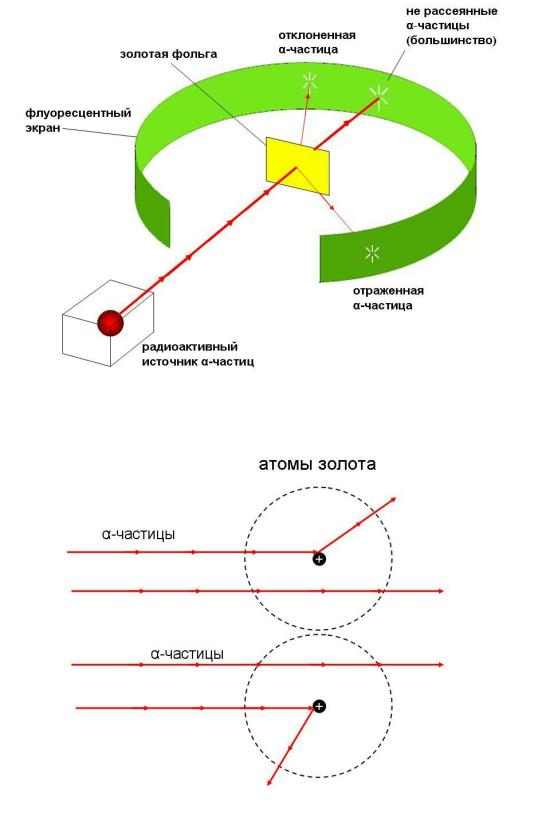
Рисунок 14. 4

Рис. 14.4. Опыт Э. Резерфорда. Поток альфа-частиц проникает сквозь тонкую золотую фольгу толщиной приблизительно 10000 атомов. Пройдя сквозь золото, альфа-частицы вызывают вспышку при ударе об экран. По вспышкам на экране можно видеть отклонения части альфа-частиц от прямолинейной траектории.

В опыте Резерфорда поток альфа-частиц направлялся на тонкую золотую фольгу, а затем становился видимым на специальном экране со светящимся покрытием (рис 14.4).

Обнаружилось, что не все альфа-частицы проходят фольгу насквозь по прямой траектории. Некоторая их часть заметно отклонялась в сторону и даже отражалась от тонкого листа золотой фольги, как снаряд от брони! Это могло означать только одно: атомы золота не сплошные, а состоят из "разреженных" пустот (сквозь которые альфа-частицы проходят беспрепятственно) и очень плотных областей, от которых альфа-частицы отскакивают, как мячик.

Резерфорд предположил, что атом золота состоит из плотного, положительно заряженного ядра, в котором сосредоточена практически вся масса атома, и окружающих это ядро электронов (рис. 14.3б). Электроны вращаются вокруг ядра, образуя разреженный "электронный рой". Альфа-частицы относительно легко проходят сквозь разреженную область, занимаемую электронами и отражаются (или отклоняются в сторону) при столкновении с плотным ядром атома. По соотношению отклоненных и не отклоненных альфа-частиц удалось рассчитать, что размеры ядра атома золота примерно в 100000 раз меньше внешних границ атома, которыми он соприкасается с другими атомами!

Модель Резерфорда объясняла результаты эксперимента с альфа-частицами, но задавала физикам и химикам еще больше вопросов, чем было раньше. Почему при движении заряженного электрона около заряженного ядра не выделяется энергия? Как атомы "прикрепляются" друг к другу? Почему электроны не падают на ядро? Каким образом физические тела, состоящие из атомов, при нагревании испускают свет?

Эти вопросы частично прояснились только после того, как датский физик Н. Бор предложил модель атома, похожую на модель Резерфорда, но с тем отличием, что электроны располагались вокруг ядра на строго определенных, постоянных орбитах (рис. 14.3в). Эта модель напоминает устройство солнечной системы, где электроны вращаются вокруг ядра так же, как планеты вокруг Солнца.

Когда вещество нагревают, электроны поглощают энергию и переходят на более удаленные от ядра постоянные орбиты, а затем возвращаются на прежнее место, выделяя энергию строго отмеренными "порциями" (в виде света). Такая “порция” энергии (ее называют квантом света) в точности равна разнице между энергиями электрона на более высокой и менее высокой орбитах.

Изучая испускаемый нагретыми телами свет, можно выяснить, сколько постоянных электронных орбит существует в атоме и даже установить довольно сложное внутреннее устройство этих орбит.

Результаты огромного числа экспериментов и усилия физиков-теоретиков позволили получить довольно подробную информацию об атомах.

Лекция 15. Опыты Резерфорда. Планетарная модель атома. Атом Бора. Модель Бора и гипотеза де Бройля. Релятивистское обобщение модели Бора.

15.1. Опыты Резерфорда. Планетарная модель атома.

15.2. Атом Бора.

15.3. Модель Бора и гипотеза де Бройля.

15.4. Релятивистское обобщение модели Бора.

Опыты Резерфорда. Планетарная модель атома.

Опыт 15.1Опыт Резерфорда

Оборудование:

1. Естественный источник радиоактивного излучения

2. Пушка, состоящая из свинцового ящика с узкой прорезью, внутрь которого помещен радиоактивный материал.

Ход работы:

Частицы (в данном случае альфа-частицы, состоящие из двух протонов и двух нейтронов), испускаемые радиоактивным веществом во всех направлениях, кроме одного, поглощались свинцовым экраном, и лишь через прорезь вылетал направленный пучок альфа-частиц. Далее на пути пучка стояло еще несколько свинцовых экранов с узкими прорезями, отсекавших частицы, отклоняющиеся от строго заданного направления. В результате к мишени подлетал идеально сфокусированный пучок альфа-частиц, а сама мишень представляла собой тончайший лист золотой фольги. В нее-то и ударял альфа-луч. После столкновения с атомами фольги альфа-частицы продолжали свой путь и попадали на люминесцентный экран, установленный позади мишени, на котором при попадании на него альфа-частиц регистрировались вспышки.

Выводы: В ходе опыта можно убедиться в каком количестве и насколько альфа-частицы отклоняются от направления прямолинейного движения в результате столкновений с атомами фольги.

Серьезный удар по модели атома Томсона нанесли результаты опытов по рассеянию α - частиц (по современным представлениям – ядер атома гелия) на тонких металлических (золотых) фольгах. Эти опыты были проведены Э.Резерфордом с сотрудниками. Суть этих опытов заключается в следующем. При прохождении через фольгу α - частицы испытывают рассеяние и отклоняются от своего первоначального движения.

Оказалось, что большая часть α - частиц проходит через фольгу, отклоняясь на небольшие углы, однако некоторое количество (примерно одна из десяти тысяч) α – частиц рассеивается на углы порядка 90⁰ и даже иногда вплоть до 180⁰. Объяснить такие результаты в модели рассеяния на атоме Томсона даже с учетом многократного накопления отклонений на малые углы оказывается принципиально невозможным4. Единственным способом объяснить полученные данные является предположение о наличии внутри атома области компактного расположения всего положительного заряда, т.е. предположение о существовании атомного ядра.

Рис 15. 1

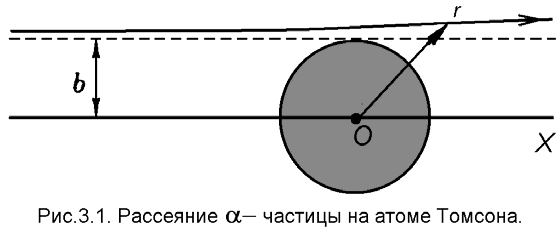Рассмотрим теперь процесс рассеяния на атоме Томсона и определим максимально возможный угол отклонения, на который может отклониться α - частица. Мы ограничимся рассмотрением рассеяния на положительно заряженном остове атома, исключив из рассмотрения электроны. Их учет, очевидно, может лишь уменьшить величину угла рассеяния. Схема процесса рассеяния приведена на рис.15.1. Атомный остов имеет заряд Z и характеризуется размером R. Характерное значение энергии α – частицы Е _α =5 МэВ⁵. Частица, рассеивающаяся на ядре, характеризуется значением прицельного параметра b. Мы ожидаем, что максимально возможный угол отклонения будет малым, поэтому траекторию движения α - частицы можно считать почти прямолинейной.

Направим ось OX вдоль вектора начальной скорости α - частицы и попытаемся определить теперь импульс, который она приобретает в направлении, перпендикулярном своему движению:

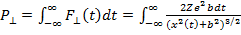(15.1)

Здесь F⊥- cила, действующая на α - частицу в направлении, перпендикулярном движению, множитель «2» - заряд α - частицы. Вводя скорость движения частицы вдоль траектории v_α, и переходя от интегрирования по времени к интегрированию вдоль траектории α - частицы, получим

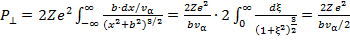(15.2)

Мы учли также, что значение интеграла в последнем выражении равно единице. Угол

отклонения определим как отношение импульса P_⊥к начальному импульсу частицы:

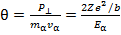(15.3)

Здесь 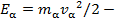кинетическая энергия α - частицы.

Мы получили интересный результат – угол рассеяния равен отношению потенциальной энергии взаимодействия α - частицы и атомного остова при их максимальном сближении (в нашем приближении прямолинейной траектории это прицельный параметр) к кинетической энергии α - частицы. Полученное выражение справедливо для значений

b ≥ R . Очевидно также, что случай b = R будет соответствовать максимальному углу отклонения. Проводя численную оценку именно для этого случая и полагая, что Z = 79 (золото), а R = 10−8 см, получим θ_max ≈ 4 ⋅10^-4 . Это всего две сотых градуса.

Получить большое значение угла рассеяния «мешает» слишком большой размер атомного остова. Это единственный свободный параметр в нашей задаче. Поэтому, если мы хотим понять результаты опытов Резерфорда, мы должны резко, почти на четыре порядка, уменьшить размер области локализации положительного заряда. То есть мы вынуждены предположить, что внутри атома существует ядро размером R ≈ 10^-120 см, несущее весь положительный заряд. Поскольку размер атома составляет величину порядка ангстрема, следует предположить, что этот размер определяется атомными электронами, которые движутся в кулоновском поле ядра. Так мы приходим к планетарной модели атома, предложенной Э.Резерфордом в 1911 году. В случае простейшего атома (атома водорода) электрон движется вокруг ядра по эллиптической (в частном случае – по круговой) траектории.

Неудовлетворительность модели Резерфорда была очевидна с самого начала.

Электрон, двигаясь по круговой (или эллиптической) орбите должен излучать электромагнитные волны, терять энергию и, в конечно счете, упасть на ядро. Атом оказывается нестабильным, живущим конечное время. Однако экспериментальные факты надежно утверждают, что свободные атомы, не будучи подвергнуты какому-либо воздействию, абсолютно стабильны. Модель Резерфорда в этом смысле оказывается значительно хуже модели Томсона, в которой стабильность атома получается сама собой.

Для того чтобы окончательно внести ясность в ситуацию, надо, конечно, оценить время жизни атома относительно падения электрона на ядро. Эту задачу можно решить

аналогично уже рассмотренной нами задачи о затухании колебательного движения электрона в атоме Томсона. Однако еще проще это сделать, исходя из энергетических соображений. Используем для этого выражение для скорости потери энергии на излучение

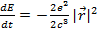(15.4)

Считая для простоты орбиту круговой, имеем 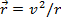, где v и r - скорость движения электрона по круговой орбите и ее радиус. Воспользовавшись уравнением движения

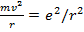(15.5)

эти величины легко выразить через полную энергию электрона. Действительно, из (15.5)

имеем

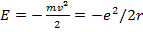(15.6)

т.е. полная энергия частицы равна кинетической энергии с обратным знаком, или половине потенциальной энергии взаимодействия с ядром. С учетом (15.6) перепишем уравнение (15.4) в виде

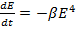(15.7)

Где 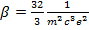. Интегрируя (15.7), найдем

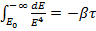(15.8)

Здесь τ - время падения электрона на ядро (полная энергия электрона при этом стремится к − ∞), E₀ - начальная энергия электрона. Из (4.7) получаем:

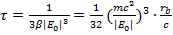(15.9)

где 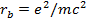- классический радиус электрона. Как видно, время жизни атома сильно зависит от величины энергии начального состояния. Сильно возбужденные состояния

(для них значение E₀ лишь немного меньше нуля) могут жить достаточно долго. Однако, для энергии E₀ ≈ −10 эВ, что характерно для большинства невозбужденных атомов, из (15.9) находим τ ~ 10⁻¹⁰ с. Собственно, эта оценка и не позволяет всерьез относиться к планетарной модели атома: электрон упадет на ядро слишком быстро.

Атом Бора.

Решающий шаг на пути развития квантовых представлений о строении атома был

сделан Н.Бором в 1913 году. Оставаясь в рамках планетарной модели, Бор предположил, что среди бесконечного множества орбит, удовлетворяющих классическим уравнениям движения, разрешены только те, для которых выполнено условие квантования момента количества движения: проекция момента на ось, перпендикулярную плоскости орбиты, кратна постоянной Планка:

L_z=nh, n=1,2,3… (15.10)

При этом, находясь на этих разрешенных орбитах электрон, не излучает вопреки законам классической механики. Излучение энергии происходит при переходе с орбиты на орбиту, причем энергия испускаемого кванта hω есть разница энергий начального конечного атомных состояний.

Сделанные выше утверждения известны как постулаты Бора. Прежде чем использовать их для расчета атомных состояний, обсудим вопрос, из каких предположений можно прийти к постулату квантования момента количества движения. При обсуждении этой проблемы мы воспользуемся сформулированным Бором принципом соответствия, согласно которому результаты, полученные в рамках квантового подхода, в предельных случаях (большие квантовые числа, малая величина энергии излучаемого кванта по сравнению с энергией системы и т.п.) должны переходить в результаты классического рассмотрения. В дальнейшем для простоты ограничимся только случаем круговых орбит.

Итак, запишем уравнения движения для электрона, обращающегося по круговой орбите вокруг ядра с зарядом Z:

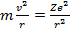(15.11)

Мы также знаем, что при движении в центрально-симметричном поле сохраняется момент количества движения. Для его z - проекции (ось z направим перпендикулярно плоскости орбиты) имеем:

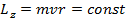(15.12)

Определим полную энергию электрона на орбите

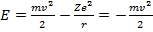(15.13)

Выразим теперь энергию электрона через орбитальный момент количества движения. Из

(15.11) и (15.12) находим

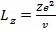(15.14)

Подставляя (15.14) в (15.13), получим

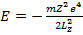(15.15)

Тогда при переходе с орбиты на орбиту изменение энергии и изменение момента количества движения связаны соотношениями:

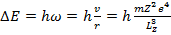(15.16)

Сопоставляя (15.15) и (15.16), получаем, что для высоких орбит в силу принципа соответствия должно быть выполнено

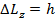(15.17)

Пусть это верно для любых орбит! Тогда, очевидно, получаем, что орбиты, по которым движется электрон, должны удовлетворять требованию

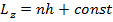(15.18)

где n - любое целое число, не равное нулю. Случай отрицательных n соответствует

вращению электрона в противоположную сторону и фактически описывает одно и то же энергетическое состояние. Естественно положить, что const = 0 , и тогда мы получаем сформулированное выше правило квантования момента.

Итак, мы имеем два уравнения – (15.10) и (15.11). Неизвестных величин тоже две – это радиус электронной орбиты и скорость движения по ней. Разрешая эти уравнения относительно r и v , получаем

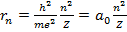(15.19)

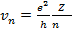(15.20)

Здесь 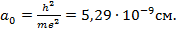- боровский радиус, фактически это размер атома водорода в основном состоянии ( n = 1). Соотношение (15.20) удобно переписать в виде

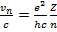(15.21)

Возникает еще одна комбинация фундаментальных констант, причем безразмерная,

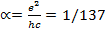. Эта величина носит название постоянной тонкой структуры. Эта постоянная имеет фундаментальный физический смысл: она определяет электрический заряд в некоторых естественных безразмерных единицах. А электрический заряд есть мера интенсивности электромагнитного взаимодействия. Малость величины α означает, что

в некотором смысле электромагнитное взаимодействие является слабым. Этот факт лежит в основе современной квантовой электродинамики, рассматривающей электромагнитное взаимодействие объектов в рамках теории возмущений по малому параметру α .

Отметим также, что наши расчеты показывают, что атом является нерелятивистской системой. При Z = 1 скорость электрона на первой боровской орбите равна 1/137 скорости света. Однако в тяжелых водородоподобных системах ситуация меняется. Например, при Z = 92 (водородоподобный ион урана) имеем 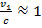. Это значит, что релятивистское обобщение модели Бора представляет значительный интерес.

Воспользовавшись выражениями (15.13) и (15.20), определим разрешенные уровни энергии электрона в атоме

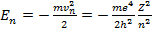(15.22)

Обозначим 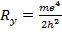. Фактически эта величина представляет собой потен-

циал ионизации атома водорода.

Определим теперь частоту излучения, испускаемого водородоподобным ионом

при переходе электрона с орбиты n на орбиту m :

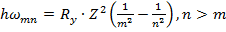(15.23)

Случай m > n соответствует поглощению кванта при переходе, наоборот, с более низкой

на более высокую орбиту. Формула (3.36) известна как обобщенная формула Бальмера и

описывает всю совокупность частот в спектрах водородоподобных систем.

Более подробно остановимся на сериальных закономерностях в спектре атома водорода ( Z = 1). Отметим, что еще в 1885 году И.Бальмером было показано, что наблюдаемые длины волн в видимой части спектра атома водорода (в то время было известно всего три таких линии, в настоящее время их число составляет несколько десятков) удовлетворяют соотношению

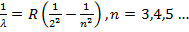(15.24)

Здесь R - постоянная Ридберга, ее численное значение R = 109700 см^-1. Соотношение

(4.23) определяет серию Бальмера в спектре водорода. Несколько позже (в 1906 году)

Лайманом аналогичная серия (серия Лаймана) была обнаружена в ультрафиолетовой

части спектра

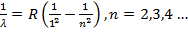(15.25)

а в 1908 году Пашеном – в инфракрасной части спектра

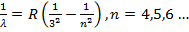(15.26)

Модель Бора находится в прекрасном согласии с этими экспериментальными данными,

действительно, формулу можно переписать в виде

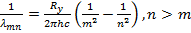(15.27)

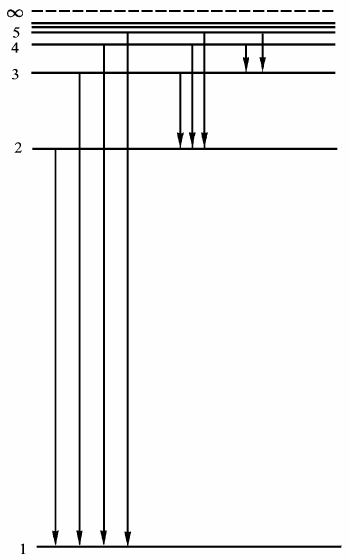
Рис 15. 2

причем теория предсказывает правильное значение для постоянной

Ридберга R = Ry/2πhc = 109700 см^-1.

Схема энергетических уровней атома

водорода и соответствующих спек-

тральных серий приведена на рис.15.2.

Линии серии Лаймана принято обозначать буквой L серии Бальмера–буквой H , номер линии в серии обозначают буквой греческого алфавит.

Например, на рис.15.1 обозначены четыре линии серии Лаймана

L _α, L _β, L _γ, L _δи три линии серии Бальмера H _α,H _β,H _γ. Первую линии любой серии принято называть головной. Например, L_α, H_α- головные линии серий Лаймана и Бальмера соответственно.

Позже в инфракрасной а затем

и в радиочастотной частях спектра

были обнаружены и другие серии,

описываемые обобщенной формулой Бальмера. В частности, переходы

на уровень m = 4 со всех более высоких n = 5,6,7,... составляют серию Брэкета, на уровень m = 5 - серию Пфунда ( n = 6,7,8...),

на уровень m = 6 - серию Хэмфри ( n = 7,8,9... ),

на уровень m = 7 - серию Хансена - Стронга ( n = 8,9,10,...).

Все эти серии носят имена ученых, впервые идентифицировавших соответствующие

спектральные линии. Отметим, что продвижение в область все больших m сильно затрудняет измерения15, в частности серия Хансена – Стронга была обнаружена только в

50-х годах ХХ века. В настоящее время в астрофизической плазме наблюдают переходы

между уровнями атомарного водорода с квантовыми числами, превышающими значения

n,m > 100. Такие сильно возбужденные состояния атома называют ридберговскими со-

стояниями, их изучение представляет как прикладной, так и общефизический интерес.

Последнее связано, в частности, с тем, что в согласно принципу соответствия Бора эти

состояния почти классические15. Поэтому появляется экспериментальная возможность

наблюдать за переходом от квантовомеханического описания атома к классическому.

Подводя итог сказанному, отметим, что модель Бора, будучи внутренне противоречивой и наполовину классической, наполовину квантовой, оказалась в прекрасном согласии с экспериментальными данными по спектру атома водорода и водородоподобных

систем. Это означает, что идея квантования момента количества движения правильно

схватывает особенности квантовомеханического описания строения атома.

Отметим также, что обобщение модели Бора на случай эллиптических орбит бы-

ло выполнено А.Зоммерфельдом17 и носит название модели атома Бора – Зоммерфельда.

Модель Бора – Зоммерфельда, существенно раздвигая возможности описания одноэлектронных систем по сравнению с первоначальной моделью Бора, является, тем не менее, своеобразным тупиком в развитии квантовой теории. В рамках такого подхода оказывается невозможным прогресс в описании строения многоэлектронных атомов, их взаимодействия с внешними электромагнитными полями и друг с другом, в частности вопрос о возникновении химической связи и образовании молекул. Более того, само описание движения электрона по некоторым разрешенным орбитам противоречит нашим квантовым представлениям о том, что такие орбиты в принципе не могут существовать, поскольку в силу соотношения неопределенностей одновременно точные значения координаты и скорости электрона определены быть не могут.