Кристаллографические способы обозначения в решетках
Для обозначения ориентации кристаллографических плоскостей направлений и точек в кристаллографической решетке принято пользоваться особыми индексами (индексы Миллера).
Для обозначения положения плоскостей пользуются индексами, устанавливаемыми из величины отрезков, отсекаемых этими плоскостями на осях координат: (на осях кристалла – ребрах элементарной ячейки) (рисунок 1.10).
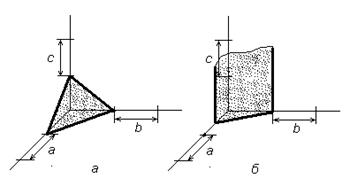 |
| Рисунок 1.10. Схема определения индексов плоскостей: а - (111); б - (210) |
Эти отрезки измеряются не в сантиметрах, но в долях ребер элементарной ячейки, принимаемых за единицу измерения вдоль каждой из осей.
Чтобы определить индексы плоскости нужно:
1. Найти отрезки, отсекаемые на трех осях, измеренные в осевых единицах.
2. Взять обратные величины этих чисел.
3. Привести отношение этих трех обратных значений к отношению трех взаимно простых чисел.
Приведенная плоскость отсекает отрезки, равные а, в и с, т.е. по единице на каждой оси. Кристаллографическое обозначение такой плоскости (111). Плоскость с координатами  , 1 и ¥ получит обозначение (210). Совокупность нескольких плоскостей в кристалле с одинаковым кристаллографическим обозначением обозначается теми же индексами, но с заключением в фигурные скобки {111} {110} и т.д.
, 1 и ¥ получит обозначение (210). Совокупность нескольких плоскостей в кристалле с одинаковым кристаллографическим обозначением обозначается теми же индексами, но с заключением в фигурные скобки {111} {110} и т.д.
В кубической решетке имеется три группы плоскостей {100}, а именно: 3 группы плоскостей куба; 4 группы плоскостей октаэдра; 6 групп плоскостей ромбического додекаэдра (рисунок 1.11).
В каждой плоскости может быть несколько кристаллографических направлений. Кристаллографическое обозначение направлений определяется в последовательности аналогичной последовательности операций, проводимых для определения индексов плоскости (рисунок 1 12). Отличие заключается в том, что опускается 2-й пункт, т.е. не берутся обратные величины отсекаемых отрезков. Обозначение направлений заключается в квадратные скобки.
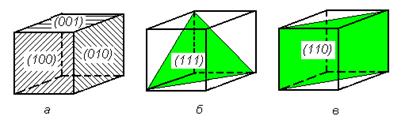 |
| Рисунок 1.11. Основные плоскости куба. Обозначения указаны на плоскостях |
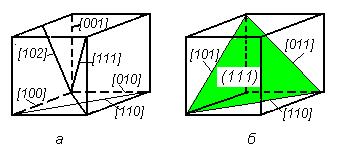 |
| Рисунок 1.12. Основные направления в кубе. Обозначения указаны на соответствующих направлениях |
В каждой плоскости может быть несколько кристаллографически равнозначных, но непараллельных направлений. Так, для кубической решетки имеются три направления [110] в плоскости октаэдра (111), два направления [100] и два направления [110] в плоскости куба (100). Положение точек в решетке обозначают с помощью координат, каждая из которых составляет часть или кратное от соответствующих осевых единиц а, в или с, причем за начало координат принимается одна из вершин ячейки. Тогда координаты точки в вершине любой другой ячейки выразятся целыми числами m, n и p.
Точки в центрах элементарных ячеек имеют координаты:
 ,
,
а в ячейке с началом координат в собственной вершине:  .
.
Атом в центре грани XY решетки гранецентрированного куба имеет координаты:  .
.
Иногда координаты точек заключают в двойные квадратные скобки:  .
.
