Общее уравнение баланса массы
В расчетах процессов химической технологии обычно используется система координат Эйлера, т. е. система координат, фиксированная относительно некоторого неподвижного объема пространства, через который протекает материальная среда. Такой объем называют контрольным, а поверхность, ограничивающую контрольный объем, именуют контрольной.
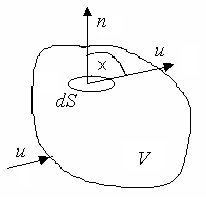 |
| Рис. 7.1. Контрольная поверхность |
Выделим на контрольной поверхности S элементарную площадку dS и восстановим к ней нормаль n (см. рис. 7.1). Тогда интегральное уравнение баланса массы (при отсутствии процессов диффузионного переноса) будет иметь вид
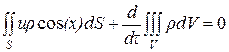 ,
,
где ρ – плотность;
τ– время;
x – угол между вектором скорости и нормалью к контрольной поверхности S.
Первый интеграл в уравнении характеризует расход вещества через контрольную поверхность, а второй – скорость накопления вещества в контрольном объеме.
Для химических аппаратов можно полагать, что вектор скорости потока перпендикулярен контрольной поверхности в точках входа и выхода и параллелен ей в остальных точках, поэтому это уравнение можно проинтегрировать:
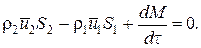
Два первых слагаемых в уравнении есть разность потоков на выходе и входе в аппарат, а третье – скорость накопления вещества в аппарате. Средняя скорость потока ū определяется выражением (по теореме о среднем)
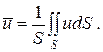
Если определить массовый расход как W=ρūS, то предпоследнее уравнение примет вид
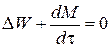 .
.
Для стационарного процесса
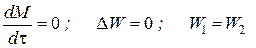
Все эти уравнения являются балансом массы по всему веществу, проходящему через контрольный объем. Уравнение баланса массы по компоненту в такой же форме можно записать так:
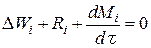 ,
,
где Ri - скорость образования или расходования компонента i за счет химической реакции.
Последнее уравнение получено в предположении отсутствия диффузионных потоков. Его можно записать для каждого компонента системы. В сумме они дадут уравнение баланса массы по всему веществу, так как åRi=0.
Таким образом, для n-компонентной системы можно составить n уравнений, причем одно уравнение общего баланса массы и (n-1) уравнение балансов массы по компонентам смеси.
При отсутствии химических реакций уравнение общего баланса массы можно записать в мольных расходах:
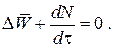
При наличии химического взаимодействия уравнение в мольных расходах по компоненту примет вид
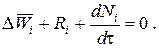
где Ni – число молей компонента.
Суммирование последнего уравнения по всем компонентам дает
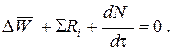
В общем случае сумма скоростей превращения компонентов (SRi) не всегда равна нулю, так как число молей в процессе реакции может изменяться. Рассмотрим пример применения уравнения материального баланса к нестационарному процессу.
Пример 7.3. При упрощенном способе производства Н3РО4 в хорошо перемешиваемую емкость, где реагирует 4000 кг/ч взвешенного в воде Са3(РО4)2, подается стехиометрическое количество 94 %-ной серной кислоты. Вместе с фосфоритной мукой подается вода, в количестве достаточном для получения при стационарном ходе процесса 40 %-ной фосфорной кислоты. Образующиеся раствор фосфорной кислоты и гипс (CaSO4·2H2O) равномерно удаляются из смесителя, так что общая масса в нем остается постоянной. Какова будет концентрация раствора фосфорной кислоты в емкости по истечении 1 часа работы, если процесс начался, когда в емкости находилось 4000 кг 20 %-ной фосфорной кислоты?
Решение: Запишем уравнение реакции и проведем стехиометрические расчеты в предположении полного превращения фосфорита:
Ca3(PO4)2+3H2SO4+6H2O=2H3PO4+3(CaSO4·2H2O).
Или в буквенном выражении:
-A-3C-6B+2F+3G=0.
Молекулярные массы компонентов реакции в кг/кмоль:
MA=310,18; MC=98,07; MB=18,02; MF=98,00; MG=172,17.
Определим коэффициент расхода по фосфориту
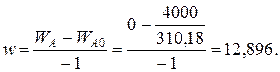
Тогда расходы компонентов будут равны (кг/ч):
WC0=WC-w· (-3) MC=0-12,896×(-3) 98,07=3791,1;
WB0=0-12,896·(-6)·18,02=1394,3;
WF=WF0+w·2·MF=0+12,896·2·98,00=2527,6;
WG=0+12,896·3·172,17=6660,8.
Определим количество воды, подаваемой с фосфоритной мукой. Составим баланс по воде
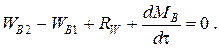
По условию задачи 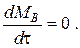 Расход воды, уходящей с фосфорной кислотой
Расход воды, уходящей с фосфорной кислотой
WB2=WF(1-0,4)/0,4=2527,6(1-0,4)/0,4=3791,4 кг/ч.
Расход воды, приносимой с серной кислотой
WB1=WC(1-0,94)/0,94+W’B1=242+ W’B кг/ч.
Скорость образования воды по химической реакции RW=WB0=1394,3 кг/ч.
Тогда расход воды, подаваемой с фосфоритной мукой
W’B1=3791,4+1394,3-242=4943,7 кг/ч.
Составим баланс по фосфорной кислоте:
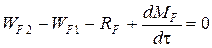 ;
;
WF1=0; WF2=xW’2; RF=WF=2527,6 кг/ч;
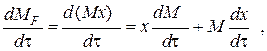
где x – концентрация фосфорной кислоты на выходе из емкости и в самой емкости;
М – общее количество реакционной смеси, кг.
W’2=WF+WB2=2527,6+3791,4=6319 кг/ч.
Для определения общего количества реакционной смеси (М) составим уравнение баланса по всему веществу:

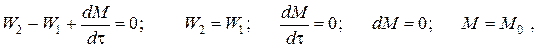
где M0 – начальное количество вещества в емкости; М0=4000 кг.
Тогда
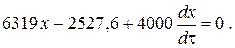
После разделения переменных 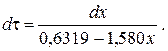
Проинтегрируем полученное уравнение в пределах от 0 до t и от 0,2 до x. После преобразований получим x=0,4-0,2exp(-1,580t).
За время 1 час концентрация фосфорной кислоты станет равной
x=0,4-0,2exp(-1,580)=0,3588, или 35,88 %.
Проверка физического смысла полученного решения дает:
при 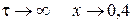 .
.
