Строение металлического слитка
Кристаллы, образующие в процессе затвердевания металла, могут иметь различную форму в зависимости от скорости охлаждения, характера и количества примесей. Чаще в процессе кристаллизации образуются разветвленные (древовидные) кристаллы, получившие название дендритов (рис. 15). При образование кристаллов их развитие идет в основном в направлении перпендикулярном к плоскостям с максимальной плотностью упаковки атомов. В результате чего сперва появляются оси первого порядка, затем перпендикулярно к ним оси второго порядка, затем третьего и так далее. Дендритное строение характерно для макро- и микроструктуры литого металла (сплава). 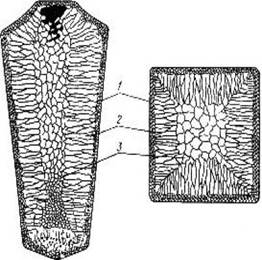
У поверхности слитка, в результате большой скорости охлаждения образуется тонкий слой мелких равноосных кристаллов, затем по мере удаления от поверхности образуются зона удлиненных дендритных кристаллов по направлению отвода тепла, т.е. перпендикулярно стенкам изложницы. В случае медленного охлаждения могут образоваться в середине слитка равноосные зерна с дендритной структурой (рис.16). Хотя зона столбчатых кристаллов обладает высокой плотностью, на границах эта плотность резко уменьшается, что может привести к возникновению трещин при ковке или прокатке. Поэтому для малопластичных металлов, в том числе для стали, развитие столбчатых кристаллов не желательно. Наоборот, для получения более плотного слитка у пластичных металлов (например, меди и ее сплавов) желательно распространение зоны столбчатых кристаллитов по всему объему слитка. При фасонном литье стремятся получить мелкозернистую равноосную структуру.
Жидкий металл имеет большой удельный объем, чем твердый; поэтому в той части слитка, которая застывает в последнюю очередь, образуется пустота - усадочная раковина. Усадочная раковина обычно окружена наиболее загрязненной частью металла, в которой после затвердевания образуются микро- макропоры и пузыри.
11. Компонент составная часть, элемент чего-либо
ФИЗИКО-ХИМИЧЕСКИЙ АНАЛИЗ, изучает зависимости между составом и св-вами макроскопич. систем, составленных из неск. исходных в-в (компонентов). Для физико-химического анализа характерно представление этих зависимостей графически, в виде диаграммы состав-свойство; применяют также таблицы числовых данных и аналит. записи. T. к. св-ва системы зависят не только от ее состава, но и от др. факторов, определяющих состояние системы,- давления, т-ры, степени дисперсности, на-пряженностей гравитац. и электромагн. полей, а также времени наблюдения,- то в общей форме говорят о диаграммах фактор равновесия - св-во, или о физ.-хим. (химических) диаграммах. На этих диаграммах все хим. процессы, происходящие в системах при изменении к.-л. фактора равновесия, как то - образование и распад хим. соед., появление и исчезновение твердых и (или) жидких р-ров и т. п., выражаются как геом. изменения комплекса линий, пов-стей и точек, к-рый образует диаграмму. Поэтому анализ геометрии диаграмм позволяет делать заключения о соответственных процессах в системе.Два осн. принципа физико-химического анализа были сформулированы Н.С. Курнаковым. Согласно принципу соответствия, каждой совокупности фаз, находящихся в данной системе в равновесии в соответствии с фаз правилом, на диаграмме отвечает определенный геом. образ. На основании этого принципа Н.С. Курнаков определил физико-химический анализ как геом. метод исследования хим. превращений.Второй осн. принцип физико-химического анализа, наз. принципом непрерывности, формулируется след. образом: при непрерывном изменении параметров, определяющих состояние системы, св-ва отдельных ее фаз изменяются непрерывно. Св-ва же системы в целом изменяются также непрерывно, но при условии, что не возникают новые фазы и не исчезают старые; если же число фаз меняется, то изменяются и св-ва системы, причем, как правило, скачкообразноТретий принцип физико-химического анализа был предложен Я.Г. Горощенко. Он утверждает, что любой набор компонентов, независимо от их числа и физ.-хим. св-в, может составить систему (принцип совместимости). Из него следует, что диаграмма любой системы содержит все элементы частных систем (подсистем), из к-рых она составлена. В общей системе элементы трансляции частных систем совмещаются с геом. образами на хим. диаграмме, возникающими как отображение процессов, протекающих с участием всех компонентов общей системы.
Сте́пени свобо́ды — характеристики движения механической системы. Число степеней свободы определяет минимальное количество независимых переменных (обобщённых координат), необходимых для полного описания движения механической системы. Также число степеней свободы равно полному числу независимых уравнений, полностью описывающих динамику системы.
13. Диаграммы состояния используют в материаловедении, металлургии, нефтепереработке, химической технологии (в частности, при разработке методов разделения веществ), производствах электронной техники и микроэлектроники и т. п. С ее помощью определяют направленность процессов, связанных с фазовыми переходами, осуществляют выбор режимов термообработки, отыскивают оптимальные составы сплавов и т. п.
Теоретическими основами построения и интерпретации диаграмм состояния равновесных систем являются: 1) условие фазового равновесия, согласно которому химические потенциалы μi каждого i-го компонента во всех фазах при равновесии равны; 2) условие химического равновесия, согласно которому сумма химических потенциалов вступающих в реакцию веществ при равновесии равна аналогичной сумме для продуктов реакции; 3) фаз правило Гиббса, согласно которому число компонентов К, число фаз Ф и вариантность системы v (т.е. число независимых параметров состояния, которые можно в определенных пределах изменять без изменения числа и природы фаз) связаны соотношением: v = К — Ф + 2. Цифра 2 означает, что учитываются только два интенсивных параметра состояния - температура и давление. Если учитываются и другие параметры, например, напряженности электромагнитного или гравитационного полей, вариантность системы соответственно увеличивается. Различают нонвариантные (v = 0), моновариантные (v = 1), дивариантные (v = 2) и т. д. состояния (равновесия); 4) правило о соприкасающихся пространствах состояния, согласно которому если два разных пространства состояния (поля в случае плоской диаграммы) соприкасаются по линии, то они различаются между собой на одну фазу, если поля соприкасаются в точке, то состояния различаются на две фазы.
Для построения диаграммы состояния расчетным путем необходимо знать зависимости химических потенциалов всех компонентов системы от Т, р и состава фаз. Приближенные методы расчета с применением ЭВМ интенсивно развиваются, в частности, для многокомпонентных сплавов. Однако пока диаграммы состояния строят на основе экспериментальных данных, получаемых главным образом термическим анализом, который позволяет определять зависимости температур плавления или кристаллизации от состава, а также изучением равновесий жидкость - пар и жидкость - жидкость. Широко используют рентгеновский фазовый анализ, данные о микроструктуре затвердевших расплавов, измерения физических свойств фаз (см. Диаграмма состав-свойство). Изучение диаграмм состояния составляет основное содержание физико-химического анализа.
14. Диаграмма состояния двухкомпонентных сплавов, образующих эвтектику. Анализ диаграммы.(диаграмма состояния 1 рода)
Диаграмма состояния и кривые охлаждения типичных сплавов системы представлены на рис. 5.3.
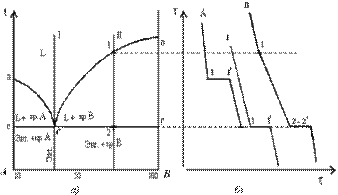
Рис. 5.3. Диаграмма состояния сплавов с отсутствием растворимости компонентов в твердом состоянии (а) и кривые охлаждения сплавов (б)
Проведем анализ диаграммы состояния.
1. Количество компонентов: К = 2 (компоненты А и В);
2. Число фаз: f = 3 (кристаллы компонента А, кристаллы компонента В, жидкая фаза).
3. Основные линии диаграммы:
линия ликвидус acb-это тем-ра выше которой сплавы находятся в жидком состоянии, состоит из двух ветвей, сходящихся в одной точке;
линия солидус ecf-это тем-ра ниже которой сплавы находятся в твердом состоянии, параллельна оси концентраций стремится к осям компонентов, но не достигает их;
4. Типовые сплавы системы.
а) Чистые компоненты, кристаллизуются при постоянной температуре, на рис 5.3 б показана кривая охлаждения компонента А.
б). Эвтектический сплав – сплав, который плавится при минимальной температуре для сплавов данной системы, соответствующий концентрации компонентов в точке с -эвтектическая точка (сплав I). Кривая охлаждения этого сплава, аналогична кривым охлаждения чистых металлов (рис. 5.3 б)
Эвтектика – равномерная механическая смесь одновременно закристолизовавшихся зерен обоих компонентов. При образовании сплавов механических смесей эвтектика состоит из кристаллов компонентов А и В: Эвт. (кр. А + кр. В) Процесс кристаллизации эвтектического сплава: до точки 1 охлаждается сплав в жидком состоянии. При температуре, соответствующей точке 1, начинается одновременная кристаллизация двух разнородных компонентов. На кривой охлаждения отмечается температурная остановка, т.е. процесс идет при постоянной температуре, так как согласно правилу фаз в двухкомпонентной системе при наличии трех фаз (жидкой и кристаллов компонентов А и В) число степеней свободы будет равно нулю 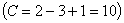 . В точке 1/ процесс кристаллизации завершается. Ниже точки 1/ охлаждается сплав, состоящий из дисперсных разнородных кристаллов компонентов А и В.
. В точке 1/ процесс кристаллизации завершается. Ниже точки 1/ охлаждается сплав, состоящий из дисперсных разнородных кристаллов компонентов А и В.
в) Другие сплавы системы аналогичны сплаву II, кривую охлаждения сплава см на рис 5.3.б. Процесс кристаллизации сплава II: до точки 1 охлаждается сплав в жидком состоянии. При температуре, соответствующей точке 1, начинают образовываться центры кристаллизации избыточного компонента В. На кривой охлаждения отмечается перегиб (критическая точка), связанный с уменьшением скорости охлаждения вследствие выделения скрытой теплоты кристаллизации. На участке 1–2 идет процесс кристаллизации, протекающий при понижающейся температуре, так как согласно правилу фаз в двухкомпонентной системе при наличии двух фаз (жидкой и кристаллов компонента В) число степеней свободы будет равно единице 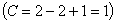 . При охлаждении состав жидкой фазы изменяется по линии ликвидус до эвтектического. На участке 2–2’ кристаллизуется эвтектика (см. кристаллизацию эвтектического сплава). Ниже точки 2’ охлаждается сплав, состоящий из кристаллов первоначально закристаллизовавшегося избыточного компонента В и эвтектики. Для сплавов образующих эвтектику физико-механические св-ва меняются по линейной зависимости. Эвтектические сплавы имеют хорошие линейные св-ва, хорошо обрабатываются резанием.
. При охлаждении состав жидкой фазы изменяется по линии ликвидус до эвтектического. На участке 2–2’ кристаллизуется эвтектика (см. кристаллизацию эвтектического сплава). Ниже точки 2’ охлаждается сплав, состоящий из кристаллов первоначально закристаллизовавшегося избыточного компонента В и эвтектики. Для сплавов образующих эвтектику физико-механические св-ва меняются по линейной зависимости. Эвтектические сплавы имеют хорошие линейные св-ва, хорошо обрабатываются резанием.
15. Диаграмма состояния для случая полной взаимной растворимости компонентов в твердом состоянии. Анализ диаграммы.( диаграмма состояния 2 рода)
Диаграмма состояния и кривые охлаждения сплавов системы представлены на рис. 5.1.
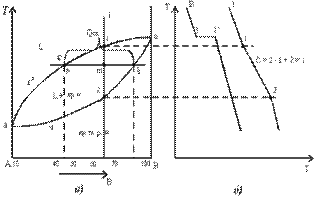
Рис.5.1 Диаграмма состояния сплавов с неограниченной растворимостью компонентов в твердом состоянии (а); кривые охлаждения типичных сплавов (б)
Сначала получают термические кривые. Полученные точки переносят на диаграмму, соединив точки начала кристаллизации сплавов и точки конца кристаллизации, получают диаграмму состояния.
Проведем анализ полученной диаграммы.
1. Количество компонентов: К = 2 (компоненты А и В).
2. Число фаз: f = 2 (жидкая фаза L, кристаллы твердого раствора 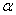 )
)
3. Основные линии диаграммы:
-acb – линия ликвидус, выше этой линии сплавы находятся в жидком состоянии;
-adb – линия солидус, ниже этой линии сплавы находятся в твердом состоянии.
4. Характерные сплавы системы:
Чистые компоненты А и В кристаллизуются при постоянной температуре, кривая охлаждения компонента В представлена на рис. 5.1,б.
Остальные сплавы кристаллизуются аналогично сплаву I, кривая охлаждения которого представлена на рис. 5.1, б. У сплавов образующих твердые растворы физико-механические св-ва меняются по плавным кривым. Они отличаются низкой электропроводностью, обрабатываются давлением, хуже резанием.
16. Диаграмма состояния для компонентов ограниченно растворимых друг в друге. Анализ диаграммы. ( диаграмма состояния 3 рода)
Диаграмма состояния и кривые охлаждения типичных сплавов системы представлены на рис.5.5.
1. Количество компонентов: К = 2 (компоненты А и В);
2. Число фаз: f = 3 (жидкая фаза и кристаллы твердых растворов 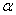 (раствор компонента В в компоненте А) и
(раствор компонента В в компоненте А) и 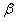 ( раствор компонента А в компоненте В));
( раствор компонента А в компоненте В));
3. Основные линии диаграммы:
линия ликвидус acb, состоит из двух ветвей, сходящихся в одной точке;
линия солидус аdcfb, состоит из трех участков;
dm – линия предельной концентрации компонента В в компоненте А;
fn – линия предельной концентрации компонента А в компоненте В.
4. Типовые сплавы системы.
При концентрации компонентов, не превышающей предельных значений (на участках Аm и nВ), сплавы кристаллизуются аналогично сплавам твердым растворам с неограниченной растворимостью, см кривую охлаждения сплава I на рис. 5.5 б. При концентрации компонентов, превышающей предельные значения (на участке dcf), сплавы кристаллизуются аналогично сплавам механическим смесям, см. кривую охлаждения сплава II на рис. 5.5 б.
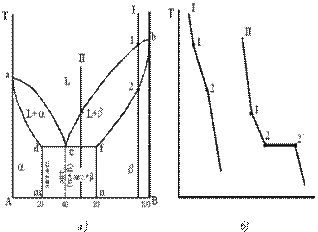
Рис. 5.5 Диаграмма состояния сплавов с ограниченной растворимостью компонентов в твердом состоянии (а) и кривые охлаждения типичных сплавов (б)
Сплав с концентрацией компонентов, соответствующей точке с, является эвтектическим сплавом. Сплав состоит из мелкодисперсных кристаллов твердых
17.Диаграмма состояния для случая образования устойчивого химического соединения. Анализ диаграммы. ( диаграмма состояния 4 рода)
Диаграмма состояния сплавов представлена на рис. 5.6.
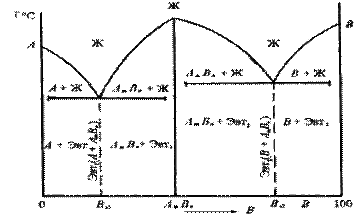
Рис. 5.6. Диаграмма состояния сплавов, компоненты которых образуют химические соединения
Диаграмма состояния сложная, состоит из нескольких простых диаграмм. Число компонентов и количество диаграмм зависит от того, сколько химических соединений(х.с.- рассматривается как самостоятельный компонент способный образовать сплавы с каждым из исходных компонентов) образуют основные компоненты системы. Число фаз и вид простых диаграмм определяются характером взаимодействия между компонентами.
Эвт1 (кр. А + кр. AmBn);
Эвт2 (кр. B + кр. AmBn).
У сплавов образующих химическое соединение и эвтектику физико-химические св-ва меняются по линейной зависимости и представляют среднее из св-в компонентов и хим-х соединений.
