Схема оценки коэффициента корреляции

Оценка корреляции	Величина коэффициента при наличии
Прямая корреляция	Обратная корреляция
Малая (низкая, слабая)	от 0,0 до +0,29	от 0,0 до -0,29
Средняя	от 0,3 до +0, 69	от 0,3 до -0, 69
Большая (высокая, сильная)	от 0,7 до +1,00	от 0,7 до -1,00

-/-/-/-/-/-/-/-/-/-/-/-/-/-/-/-/-/-/-/-/-/-/-/-/-/-/-/-/-/-/-/-/-/-/-/-/-/-/-/-/-/-/-/-/-/-/-/-/-/-/-/-/-/-/-/-/-/-/-/-/-/-/-/-/-/-/-/-/-/-

3. Оценка достоверности коэффициента корреляции по Пирсену.

Значения коэффициента корреляции Пирсена интерпретируются исходя из его абсолютных значений. Возможные значения коэффициента корреляции варьируют от 0 до ±1. Чем больше абсолютное значение r_xy – тем выше теснота связи между двумя величинами. r_xy = 0 говорит о полном отсутствии связи. r_xy = 1 – свидетельствует о наличии абсолютной (функциональной) связи. Если значение критерия корреляции Пирсона оказалось больше 1 или меньше -1 – в расчетах допущена ошибка.

Для оценки тесноты, или силы, корреляционной связи обычно используют общепринятые критерии, согласно которым абсолютные значения r_xy < 0.3 свидетельствуют о слабой связи, значения r_xy от 0.3 до 0.7 - о связи средней тесноты, значения r_xy > 0.7 - о сильной связи.

Более точную оценку силы корреляционной связи можно получить, если воспользоваться таблицей Чеддока:

Абсолютное значение rxy	Теснота (сила) корреляционной связи
менее 0.3	Слабая
от 0.3 до 0.5	Умеренная
от 0.5 до 0.7	Заметная
от 0.7 до 0.9	Высокая
более 0.9	весьма высокая

Оценка статистической значимости коэффициента корреляции r_xy осуществляется при помощи t-критерия, рассчитываемого по следующей формуле:

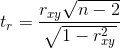
Полученное значение t_r сравнивается с критическим значением при определенном уровне значимости и числе степеней свободы n-2. Если t_r превышает t_крит, то делается вывод о статистической значимости выявленной корреляционной связи.

4. Методика вычисления и оценка коэффициента ранговой корреляции.

Коэффициент ранговой корреляции Спирмена - это непараметрический метод, который используется с целью статистического изучения связи между явлениями. В этом случае определяется фактическая степень параллелизма между двумя количественными рядами изучаемых признаков и дается оценка тесноты установленной связи с помощью количественно выраженного коэффициента.

Практический расчет коэффициента ранговой корреляции Спирмена включает следующие этапы:

1) Сопоставить каждому из признаков их порядковый номер (ранг) по возрастанию (или убыванию).

2) Определить разности рангов каждой пары сопоставляемых значений.

3) Возвести в квадрат каждую разность и суммировать полученные результаты.

4) Вычислить коэффициент корреляции рангов по формуле:

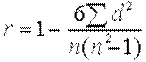
где 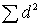- сумма квадратов разностей рангов, а 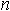- число парных наблюдений.

Коэффицент ранговой корреляции целесообразно применять при наличии небольшого количества наблюдений. Данный метод может быть использован не только для количественно выраженных данных, но также и в случаях, когда регистрируемые значения определяются описательными признаками различной интенсивности.

Рекомендации по применению метода ранговой корреляции (метод Спирмена):

· когда нет необходимости в точном установлении силы связи, а достаточно ориентировочных данных;

· когда признаки представлены не только количественными, но и атрибутивными значениями;

· когда ряды распределения признаков имеют открытые варианты (например, стаж работы до 1 года и др.).

Коэффициент корреляции Спирмена обладает следующими свойствами:

1. Коэффициент корреляции может принимать значения от -1 до 1, причем при rs=1 имеет место строго прямая связь, а при rs= -1 – строго обратная связь.

2. Если коэффициент корреляции отрицательный, то имеет место обратная связь, если положительный, то – прямая связь.

3. Если коэффициент корреляции равен нулю, то связь между величинами практически отсутствует.

4. Чем ближе модуль коэффициента корреляции к единице, тем более сильной является связь между измеряемыми величинами.

5.Оценка достоверности коэффициента корреляции по Спирмену.

При использовании коэффициента ранговой корреляции условно оценивают тесноту связи между признаками, считая значения коэффициента равные 0,3 и менее, показателями слабой тесноты связи; значения более 0,4, но менее 0,7 - показателями умеренной тесноты связи, а значения 0,7 и более - показателями высокой тесноты связи.

Если абсолютное значение коэффициента корреляции составляет 0,0, то это значит, что связь между изучаемыми признаками или явлениями отсутствует, а если коэффициент корреляции равен 1,0, то это свидетельствует о наличии полной корреляционной связи или функциональной связи между изучаемыми признаками или явлениями.

Коэффициент корреляции считается достоверным, если его абсолютная величина в три и более раз превышает величину своей ошибки.

Оценка достоверности рангового коэффициента корреляции Спирмена производится на основании t-критерия Стьюдента, который вычисляется по формуле:

.

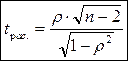Вывод: Если значение t_расч.<t_крит., то коэффициент ранговой корреляции статистически недостоверен. Следовательно, в генеральной совокупности не будет существовать взаимосвязи между изучаемыми показателями.

Если же t_расч.˃t_кр, то выборочный коэффициент достоверен. Следовательно, в генеральной совокупности между изучаемыми показателями будет существовать взаимосвязь.