Кинетические уравнения реакций различных порядков

1. Реакции первого порядка.

К этим реакциям относятся реакции изомеризации, термического разложения веществ, реакции радиоактивного распада и многие бимолекулярные реакции при условии, что концентрация одного из реагирующих веществ поддерживается постоянной.

Для реакции типа А → В скорость выражается уравнением:

V = - 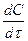= К * С_А (2.15)

Или разделив переменные

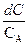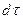- = К * и проинтегрировав данное уравнение, получим:

- ln C_A = K * τ + const

Значение const можно определить из начальных условий. При τ = 0 концентрация вещества А в данный момент (С_А) будет равна концентрации вещества А в начальный момент времени (С_О,А). Следовательно, const = - ln C_О,A В этом случае

- ln C_A = К * τ - ln C_О,А

Или

- ln C_A + ln C_О,А = К * τ

Из полученного выражения

К = 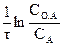(2.16)

Это уравнение называется уравнением реакции первого порядка. Оно дает возможность вычислить концентрацию реагирующего вещества в любой момент времени по известной величине константы скорости или, наоборот, найти константу скорости реакции при заданной температуре путем определения концентрации в любой момент времени.

Если через Сх обозначить уменьшение концентрации исходного вещества к моменту времени τ, то уравнению можно придать вид:

К = 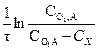(2.17)

Для характеристики скорости реакции первого порядка наряду с константой скорости часто пользуются величиной, называемой периодом полураспада (τ^1/2), то есть временем, необходимым для того, чтобы прореагировало половина взятого вещества. Принимая 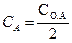, из уравнения (2.16) находим:

К = 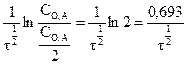или 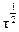= 0,693/К (2.18)

Из уравнения видно, что время полураспада для реакции первого порядка не зависит от количества вещества.

Следует также отметить, что константа скорости в уравнениях первого порядка имеет размерность обратного времени [K] = С^-1, мин^-1

2. Реакции второго порядка.

К ним принадлежит большинство бимолекулярных реакций и некоторые тримолекулярные. Реакции второго порядка можно представить схемой А + В → продукты реакции.

Скорость такой реакции определяется уравнением:

V = - 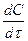= К * С_А * С_В

Где С_{А и} С_В – концентрации реагирующих веществ в момент времени τ.

Рассмотрим простейший случай, когда концентрации двух реагирующих веществ одинаковы, тогда

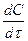- = К * С² (2.20)

Разделить переменные 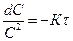и проинтегрировав уравнение

(С^-2 * dc = 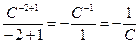) получим

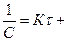const (2.21)

При τ = 0, С = Со, const = 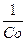, тогда 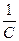- 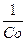= Кτ или

К = 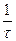( 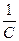- 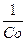) = 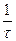( 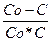) (2.22)

Заменив С на С_о - С_х, получим:

К = 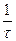( 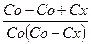) = 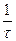( 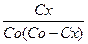) (2.23)

При условии С_А ≠ С_В уравнение скорости реакции в дифференциальной форме имеет вид:

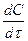- = К * С_А * С_В = К (С_О,А - С_Х)(С_О,В - С_Х)

Разделив переменные

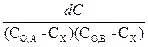= - К * dτ и проинтегрировав, получим:

К = 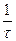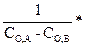ln 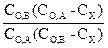(2.24)