Все самопроизвольно протекающие процессы

До XIX века попытка управления превращениями плохо реализовывалась, пока в химии не сформировалось еще одно направление: изучение законов превращения энергии, которая сопровождает химические реакции.

Термин " ЭНЕРГИЯ " был предложен врачом Томасом Юнгом в 1807 году [1] и обозначает "внутренняя работа ". Некоторое время спустя другой немецкий врач Юлиус Майер (1811 - 1878) [2] и английский физик Джеймс Прескот Джоуль (1818-1889) показали, что теплота и работа могут взаимно переходить друг в друга и являются двумя различными способами передачи энергии [3].

Таким образом, работы Юнга, Майера и Джоуля определили развитие во второй половине XIX века фундаментального научного знания ТЕРМОДИНАМИКИ.

Термодинамику можно назвать философией естественных наук. Она изучает законы превращения энергии, которыми сопровождаются ВСЕ!!! физические и химические процессы. Её рождению способствовали также работы по изучению энергетических эффектов химических реакций, опубликованные в 1840 году российским учёным, академиком Германом Ивановичем Гессом (1802-1850) [4].

Термодинамика изучает (или точнее математически оценивает) возможность протекания процесса [5]. Если кинетика оценивает протекание реакции во времени, т.е. ее скорость, то термодинамика отвечает только на вопрос: возможен ли процесс в данных условиях или нет? Под возможностью обычно понимается самопроизвольность, т.е. без подведения дополнительной энергии извне.

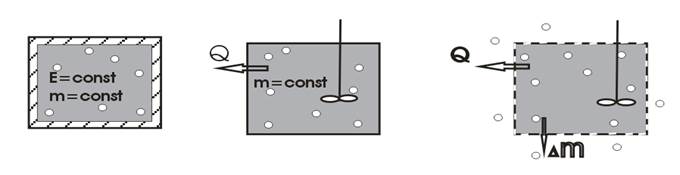
изолированная закрытая открытая

Для оценки тепловых эффектов с помощью термодинамических закономерностей необходимо определиться с некоторыми понятиями:

СИСТЕМА – совокупность материальных объектов, отделенных от окружающей среды каким - либо образом (изолированная, закрытая, открытая). Изолированная система - не имеет связи, т.е. обмена с окружающей средой ни массой (веществом), ни энергией. Закрытая система - имеет связь, обменивается с окружающей средой только энергией, например, радиатор в комнате. Открытая система - имеет связь, обменивается и массой (веществом) и энергией, например, человек. Необходимо отметить, что ничего абсолютного в нашем мире не существует, в том числе и абсолютно изолированные системы. Изолированная система – это лишь модель, а строго говоря, таких систем не существует.

Например, когда мы проводим химическую реакцию между водными растворами в химическом стакане, системой является содержимое стакана и приповерхностный слой стакана, но не сам стакан. Стакан, воздух и все окружающие предметы называются окружающей средой.

ФАЗА – часть системы с одинаковыми химическими и термодинамическими свойствами, имеющая границу раздела.

ПРИМЕРЫ: если система - смесь газов - кислород, азот, углекислый газ, то фаза - область однородности - газовая; если система - насыщенный раствор соли относительно осадка, фазы в системе две: жидкая (раствор) и твердая (кристаллы соли).

Фазу вещества всегда можно охарактеризовать некоторым набором макроскопических свойств, например, твердостью, плотностью или отсутствием электрической проводимости.

КОМПОНЕНТ -часть системы, которая может быть удалена из неё и существовать независимо от системы (например, раствор NaС1 в воде: система «соль – вода», фаза – «жидкая», компоненты – «соль (NaCl)» и «вода», но не элементы Na и С1!

Различают системы гомогенные и гетерогенные. Гомогенные системы состоят из одной фазы, а гетерогенные – из нескольких фаз.

В термодинамике конкретную систему определяют ее состоянием. Состоянием системы называют совокупность всех физических и химических свойств системы. Различают параметры состояния системы и функции состояния системы.

Параметры состояния системы (интенсивные свойства) – свойства, не зависящие от массы системы, выравнивающиеся при контакте систем и их можно экспериментально измерить (температура, давление, плотность, концентрация). Они характеризуют только данное состояние системы (в данный момент времени), никак не свидетельствуя о предшествующих состояниях.

Функции состояния (экстенсивные свойства) – зависят от массы системы и не поддаются непосредственному экспериментальному измерению (объем, масса, теплоемкость, внутренняя энергия, энтальпия, энтропия, термодинамические потенциалы). Экстенсивные свойства в термодинамике принято называть функциями состояния системы. Одно из основных свойств любой ф-ции состояния – независимость ее изменения от способа изменения состояния системы.

Состояние системы можно описать с помощью уравнения состояния, которое включает в себя функции и параметры состояния. Например, уравнение состояния идеального газа: PV=nRT. К сожалению, точного уравнения состояния для реальных систем не существует, т.к. для его вывода необходимо учитывать огромное количество разнообразных факторов, влияющих на состояние реальной системы, а это невозможно. Уравнения, описывающие реальные системы выводятся с достаточно большим числом допущений и упрощений, и поэтому описывают состояние реальных систем неточно.

Переход системы из одного состояния в другое называется процессом. В результате процесса состояние системы и параметры ее состояния изменяются.

Хотя в термодинамике рассматриваются не только равновесные состояния, нам придется иметь дело лишь с системами, находящимися в состоянии равновесия. Это означает, что температура, плотность, давление и другие подобные характеристики системы принимают одинаковые значения во всех точках системы, а в отношении химических систем это означает, что равновесие в реакции достигнуто во всех точках системы.

1 з-н термодинамики. Сохранение энергии.

Подобно тому, как в химии для стехиометрического описания реакций применяются представления о сохранении массы, термодинамика основывается на представлениях о сохранении энергии. Энергия не появляется ниоткуда и никуда не исчезает, она переходит из одних форм в другие.

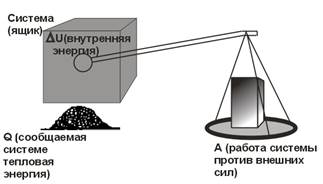
Экспериментальное обнаружение эквивалентности различных форм энергии послужило основой для вывода о том, что энергия сохраняется во всех физических и химических процессах. Представление о сохранении тепловой энергии формулируется в виде первого начала (закона) термодинамики. Принято считать, что в системе, которая получает извне определенное количество тепловой энергии Q, происходит изменение внутренней энергии ΔU; вместо этого система за счет полученной энергии может выполнить над своим окружением некоторую работу А. В общем случае поступившая в систему извне тепловая энергия может быть частично израсходована на изменение внутренней энергии системы, а частично – на выполнение работы. Математически это соотношение между тепловой энергией, внутренней энергией и работой описывается уравнением:

Q = ΔU + А.

Q и А – экспериментально измеряемые величины, а ΔU – изменение внутренней энергии системы – функция состояния, которая не поддается экспериментальному измерению, а лишь ее изменение может быть выражено через Q и А.

Q – это тепловая энергия, которая поступает в систему в процессе изменения ее состояния. Знак Q положителен, если теплота поступает в систему, и отрицателен, если теплота выделяется системой.

Работа – направленное упорядоченное движение молекул и ионов.

Теплота (теплопередача, теплоперенос) – хаотическое движение молекул и ионов.

Первое начало термодинамики относится к числу фундаментальных законов природы, которые не могут быть выведены из каких-то других законов. Первое начало термодинамики также является количественным выражением одного из важнейших законов природы – закона сохранения энергии и материи.

Когда система выполняет работу над своим окружением, принято работу А считать положительной. Обычно работу выражают в виде РΔV , где Р – внешнее давление, против которого действует система. Знак А будет отрицателен в том случае, когда работа выполняется над системой. Например, когда мы толкаем поршень насоса, накачивающего воздух в велосипедную шину, работа выполняется над воздухом в цилиндре насоса и знак этой работы будет отрицательным.

Пример.Рассчитать работу, которая осуществляется при протекании реакции

Na₃AsO₃ + 3Zn + 9НCl = AsH₃↑ + 3NaCl + 3ZnCl₂ + 3H₂O

Из 1 моль арсенита натрия Na₃AsO₃ выделяется 1 моль газообразного арсина AsH₃ , который оттесняет окружающую атмосферу и производит работу А=рΔV. Будем рассматривать арсин как идеальный газ. Пренебрегая объемом исходных реагентов можно приравнять рΔV=рV=nRT, где n – количество молей газа, R – универсальная газовая постоянная, T – абсолютная температура. Если прореагирует 1 моль арсенита натрия, то работа будет равна А = 1•8,31•298 = 2496,4 Дж.

Теперь о внутренней энергии. Под внутренней энергией обычно понимают энергию всех частиц, составляющих систему: потенциальная энергия молекул вещества (энергия, связанная с положением молекул или структурой вещества), а также кинетическая энергия, связанная с поступательным, колебательным и вращательным движением молекул. Например, для превращения 1г воды в пар при 100^оС в закрытом сосуде всего необходимо подвести к системе 540 кал тепла. Однако 499 кал тратится на изменение внутренней энергии этой системы: преодоление сил межмолекулярного притяжения между молекулами воды (известно, что молекулы пара располагаются приблизительно в 10 раз дальше друг от друга, чем молекулы жидкости) и только 41кал расходуется на совершение работы системой против атмосферного давления.

Расчёты, производимые в термодинамике, предполагают из трёх наиболее важных характеристик системы (давление, объём, температура) постоянство одного из них: при постоянном объёме - изохорные, при постоянном давлении - изобарные и при постоянной температуре - изотермические. Если оценивать работу как А= РΔV, то при V = const (изохорный процесс) А = 0, т.е. изменение внутренней энергии системы связано с получением или отдачей тепла и наоборот при подведении энергии в систему с V = const, работа системой не совершается Q_V = ΔU (А= 0) .

В тех случаях, когда экспериментальные измерения теплоты, поглощаемой или выделяемой в химической реакции, выполняются при постоянном давлении, для определения изменения внутренней энергии системы необходимо учесть работу РV, которая совершается системой над ее окружением:

Для Р = const (изобарный процесс) : ΔU = Q_P - А или U₂ -U₁ = Q_Р - Р(V₂ - V_I) , решая относительно Q_P = (U₂ + РV₂) - ( U₁ + РV₁). Q_P – тепло, поступившее в систему при постоянном давлении.

С этой целью (учесть работу) вводится определение нового понятия – энтальпии Н. Энтальпия является еще одной функцией состояния, которая определяется как Q_P с помощью уже известной нам функции состояния – внутренней энергии:

Н ≡ U + РV.

Таким образом, при изменении состояния системы в изобарном процессе происходит изменение энтальпии системы:

Q_P = (U₂ + РV₂) - ( U₁ + РV₁) = Н₂ – Н₁ , причем

если Н₂ < Н_1, то DН<0, т.е. тепло выделяется, реакция экзотермическая

если Н₂ > Н_1, то DН>0, тепло поглощается, реакция эндотермическая.

Значит, изменение энтальпии системы оказывается равным подводимой к системе теплоте только при постоянном давлении. Это объясняет тот факт, что для энтальпии часто используют другое название – теплосодержание системы.

Изменение энтальпии системы в процессе образования 1 моля сложного вещества из простых веществ называется энтальпией образования данного соединения. Измеряется в кДж/моль, обозначается D_fН или DН_обр. Для простых веществ энтальпия образования принята равной 0. Например, выражение «энтальпия образования жидкой воды равна -285,8 кДж/моль» означает, что при образовании 1 моля жидкой воды (18 г) по уравнению

Н₂О +1/2 О₂ = Н₂О

из 2 г водорода и 8 г кислорода выделяется 285,8 кДж тепловой энергии. Величина энтальпии зависит от агрегатного состояния вещества и температуры. Поэтому для удобства сравнения различных реакций по величинам тепловых эффектов эффекты указывают для стандартного состояния (298 К) с указанием агрегатного состояния вещества. В этом случае энтальпию называют стандартной энтальпией образования данного вещества и обозначают D_fН⁰ или DН²⁹⁸_обр. или DН⁰_обр. Так энтальпия образования водяного пара из водорода и кислорода равна -241,8 кДж/моль. Разность между значениями энтальпий образования жидкой и парообразной воды представляет собой энтальпию процесса испарения жидкой воды.

Второе начало термодинамики. Энтропия.

Первое начало термодинамики лишь констатирует сохранение энергии при любых превращениях, но не позволяет судить о способности физических и химических процессов к самопроизвольному протеканию. Это позволяет II НАЧАЛО ТЕРМОДИНАМИКИ.

Процесс называется самопроизвольным, если он осуществляется без каких-либо воздействий, когда система предоставлена самой себе. Например, газ может самопроизвольно расширяться, но не может самопроизвольно сжиматься в локальном объеме пространства. Направленное и упорядоченное движение молекул может самопроизвольно перейти в хаотическое движение, но обратный процесс не может происходить самопроизвольно, а только при воздействии на систему извне.

Протекание самопроизвольных процессов сопровождается рассеиванием энергии и материи в окружающей среде. При этом всякая система стремится перейти в состояние равновесия.

II начало утверждает, что природные и технологические процессы самопроизвольно могут протекать только в одном направлении – в направлении увеличения энтропии системы. При этом система стремится перейти в состояние равновесия. Напомню, что под равновесным понимают такое состояние, которое не изменяется во времени и не поддерживается какими-либо внешними факторами. При этом (самопроизвольном протекании процессов) тепло идёт от горячего тела к холодному. Газы самопроизвольно при нагревании расширяются. Например, кусок сахара при растворении распадается на молекулы сахарозы и они равномерно распространяются по всему объёму воды (чая).

Процессы, о которых мы говорим, можно разделить на термодинамически обратимые и необратимые.

Процесс называется термодинамически обратимым, если при переходе из начального состояния в конечное все промежуточные состояния оказываются равновесными. Пример – обратимая реакция гидролиза ацетата натрия

СН₃СООNa + Н₂О ↔ СН₃СООН + Na⁺ + ОН¯

Состояние 1 состояние 2

Систему можно вернуть в состояние первоначальное (1) добавлением избытка гидроксида натрия NaОН.

Процесс называется термодинамически необратимым, если

хоть одно из промежуточных состояний неравновесно.

Необратимый процесс - это реакция, в результате которой в

системе или в окружающей среде возникают неисчезающие

изменения. Пример – необратимая реакция гидролиза карбоната алюминия:

2AlCl₃ (водн. р-р) + 3Na₂CO₃ (водн. р-р) = Al₂(CO₃)₃↓ + 6NaCl

Al₂(CO₃)₃ + 6Н₂О = Al(OH)₃↓ + 3H₂O + 3CO₂↑

Угольная кислота разлагается на воду и углекислый газ, который рассеивается в окружающей среде, потому мы не можем добавить Н₂СО₃ в систему для возврата ее в исходное состояние.

В реальном необратимом процессе только часть энергии превращается в полезную работу, а другая часть - является связанной, потерянной, "обесцененной". Именно поэтому КПД тепловых машин никогда не равен 100%. Это возможно лишь, если окружающая систему среда находится при абсолютном нуле [7]:

КПД = А/Q₁ = (Q₁-Q₂)/Q₁ = (T₁ – T₂)/T₁

Т₂ = 0, КПД = Т₁/Т₁ = 1.

Но абсолютный нуль недостижим. Для характеристики этой "обесцененной" энергии, составляющей потери, Р.Д.Э. Клаузиус (немецкий учёный) ввел в 1850 году [8] новую функцию состояния системы - ЭНТРОПИЮ (S). Энтропия связана с теплотой, подводимой к системе при постоянной температуре, соотношением: ΔS =ΔQ/Т, т. е. энтропия – это элементарное (бесконечно малое) изменение тепловой энергии системы при данной постоянной температуре, измеряется в Дж/К·моль. Следовательно, данная энергия расходуется не на нагрев системы, а на другие преобразования в системе. Впервые такое толкование энтропии предложил Клаузиус. Тогда ΔQ = ΔS • Т - это и есть связанная, "обесцененная" энергия. В настоящее время энтропия используется для количественной характеристики рассеивания энергии в окружающей среде при переходе системы из 1 состояния в другое.

Если для Н (энтальпии) нельзя вычислить абсолютное значение, то для S - можно, исходя из постулата: ЭНТРОПИЯ ИНДИВИДУАЛЬНОГО КРИСТАЛЛИЧЕСКОГО ВЕЩЕСТВА ПРИ АБСОЛЮТНОМ НУЛЕ (-273^ОС) РАВНА 0 (S₀=О). Потому что при абсолютном нуле тепловое движение молекул прекращается. Этот постулат называют третьим законом термодинамики или III НАЧАЛОМ [9].

Смысловые значения энтропии:

1) Энтропия как критерий возможности, направления и предела протекания процесса в изолированной системе. В изолированных системах самопроизвольно могут протекать только такие процессы, в результате которых энтропия увеличивается и ΔS˃0. Процесс протекает самопроизвольно до тех пор, пока не наступит равновесие и энтропия примет максимальное значение, а ΔS=0.

2) Энтропия как мера связанной энергии характеризует ту часть энергии, которая не превращается в работу. Чем выше энтропия, тем выше теплота Q=ST и тем больше хаотическое движение молекул и рассеивание энергии и ниже работоспособность системы.

3) Энтропия как мера неупорядоченности в системе. Увеличение энтропии связано с усилением хаотического движения молекул и ионов. Это и понятно, ведь чтобы молекулы двигались быстрее и дальше, они должны обладать большим запасом энергии, а энтропия – это тоже энергия! Следовательно, рост энтропии связан с увеличением неупорядоченности (хаотичности) в системе. Например, в кристалле льда молекулы более упорядочены, чем в жидкой воде; две жидкости, отделенные одна от другой (т.е. несмешивающиеся), более упорядочены, чем их гомогенная смесь.

4) Энтропия как вероятность нахождения системы в данном состоянии. Количественная взаимосвязь между энтропией и термодинамической вероятностью W нахождения системы в данном состоянии выражается уравнением Больцмана

S = k•lnW,

где k – константа Больцмана. Из данного выражения следует, что энтропия тем выше, чем больше величина термодинамической вероятности. Это означает, что любая система с большей вероятностью будет находиться в состоянии, которое характеризуется высоким значением энтропии (Т.е. состоянием с большей неупорядоченностью).

Известно, что термодинамическое состояние системы характеризуется величинами давления, температуры и объёма (молярного). Эти параметры системы зависят от ее молекулярно - кинетических свойств и поэтому могут быть оценены значением вероятностного состояния системы. Под термодинамической вероятностью данного макросостояния системы понимается число микросостояний, с помощью которых можно реализовать данное макросостояние. Чем больше количество возможных микросостояний, с помощью которых можно реализовать данное макросостояние, тем более вероятным это состояние будет, следовательно, тем больше его термодинамическая вероятность. Обозначим W – термодинамическую вероятность, т.е. сумму всевозможных состояний, комбинаций, сочетаний элементов системы, которые могут соответствовать ей. Видимо, эта величина будет огромным числом, но любое огромное число можно выразить через показательную функцию как 10ⁿ, учитывая, что n - это общее обозначение и его можно заменить на S, тогда получаем, что W ~ 10^S (при этом какое бы большое не было число W, S - всегда будет меньшим). Для определения S необходимо логарифмировать значение вероятности: lgW ~ lg10^S , отсюда S ~ lgW. Именно так в 1877 году предложил интерпретировать энтропию Л. Больцман (1844 – 1906), на надгробье могилы которого на венском кладбище выгравировано: S = k·logW (где k – постоянная Больцмана).

Самопроизвольные процессы всегда идут в направлении от менее вероятного к более вероятному состоянию системы, т.е. в НАПРАВЛЕНИИ УВЕЛИЧЕНИЯ ЭНТРОПИИ. Чем более упорядочена система (например, в кристаллическом состоянии), тем меньше возможных микросостояний (отклонений от равновесного состояния) и тем меньше энтропия. По мере уменьшения упорядоченности структуры системы возрастает количество возможных микросостояний и энтропия увеличивается.

Энтропия характеризует распределение частичек в пространстве, поэтому самопроизвольно протекающие процессы всегда идут с увеличением энтропии (испарение, растворение, диффузия: S> 0, а такие процессы, как кристаллизация, конденсация протекают при S < 0).

По аналогии с энтальпией энтропия вещества находящегося при стандартных условиях (298 К) называется стандартной энтропией S⁰, но для простых веществ она не равна 0.

Изменения энтропии:

1) Энтропия увеличивается всегда, когда жидкость или твердое вещество превращаются в химической реакции в газ.

Пример:

Вещество: Na(_ТВ) Br₂(ж) H₂O(ж)

S⁰(тв, ж), Дж\(моль•К) 51,0 152,3 69,9

S⁰(г), Дж\(моль•К) 153,6 245 188,7

2) Энтропия повышается при увеличении массы частиц вещества, если другие условия неизменны.

Пример:

Вещество: F₂ Cl₂ Br₂ I₂ O O₂ O₃

S⁰, Дж\(моль•К) 203 223 245 261 161 205 238

3) Энтропия тем больше, чем сложнее химический состав вещества.

Пример:

Вещество: NaCl MgCl₂ AlCl₃

S⁰(тв), Дж\(моль•К) 72,4 89,5 167

4) Энтропия увеличивается при растворении жидкости или твердого вещества в воде или другом растворителе.

Пример:

Вещество: СН₃ОН(ж) NaCl(тв)

S⁰(тв, ж), Дж\(моль•К) 127,0 72,4

S⁰(р-р в воде), Дж\(моль•К) 132,3 115,4

5) Энтропия увеличивается по мере увеличения мягкости вещества и ослабления связей между атомами.

Пример:

Вещество: С(алмаз) Be(тв) Pb(тв) Hg(ж) Hg(г)

S⁰(тв, ж), Дж\(моль•К) 2,44 9,54 64,9 77,4 174,9

Состояние прочный твердый мягкий жидкость газ

кристалл металл металл

6) Энтропия уменьшается при растворении газов в жидком растворителе.

Пример:

Вещество: СН₃ОН (г) HCl (г)

S⁰(г), Дж\(моль•К) 236 186,7

S⁰(р-р в воде), Дж\(моль•К) 132,3 55,2

7) Энтропия ниже в твердых веществах с ковалентными связями.

Пример:

Вещество: С (алмаз) Sn серое, С (графит) Sn белое,

алмазоподобное металлическое

S⁰(тв), Дж\(моль•К) 2,44 44,8 5,7 51,5

Растения и животные – открытые системы - казалось бы вопреки II началу термодинамики самопроизвольно развиваются в сложные структуры, что сопровождается уменьшением ΔS, т.е. ΔS < 0 . По мере развития земных организмов беспорядок уменьшается. Это происходит потому, что неограниченно используется энергия солнца.
Таким образом возникло некоторое противоречие фундаментальному закону и в процессе его разрешения ученые пришли к выводу, что для открытых систем ЭНТРОПИЯ как критерий возможности протекания процесса неприемлема, его одного недостаточно.

Возникшая проблема в той или иной степени давно волновала ученых: необходима была функция, описывающая возможность самопроизвольного процесса, которая бы учитывала энергию связи атомов в соединении и перемещение этих соединений в пространстве.

Американский физик Джозайя Уиллард Гиббс (1839 - 1903) в 60-х годах 19 века ввел понятие "свободная энергия". Эта величина по решению Международного Союза Чистой и Прикладной Химии (IUPAC) называется "энергия Гиббса", а также имеет название «изобарно-изотермический потенциал». Определяется по формуле G=Н-ТS. Необходимость введения этого понятия была обусловлена тем, что измерить изменение величины свободной энергии легче, чем измерить изменение энтропии: ΔG = ΔН - ТΔS (Гиббс предложил эту формулу в 1876 году ).

Следует отметить, что свободная энергия характеризует только состояния при постоянных давлении и температуре. Они называются изобарно-изотермическими, поэтому и энергию Гиббса также рекомендовано IUPAC называть изобарно-изотермическим потенциалом. Его изменение (ΔG) в каком либо процессе позволяет предсказать возможность или невозможность его самопроизвольного протекания. При этом, если ΔG = 0 , то система находится в равновесии, если ΔG < 0 , то в системе может происходить самопроизвольный процесс, (например, взаимодействие кислоты со щёлочью), если ΔG > 0, то самопроизвольное изменение состояния системы невозможно.

Анализ формулы ΔG = ΔН – ТΔS приводит к выводу о том, что уменьшить энергию Гиббса системы можно:

1) либо путем уменьшения энтальпии системы (тепловой энергии);

2) либо путем увеличения энтропии системы.

При низкой температуре энтропия очень мало влияет на свободную энергию системы, поэтому в таких условиях уменьшение G по существо происходит за счет изменения энтальпии. Но при высоких температурах даже незначительное изменение энтропии может сильно повлиять на величину энергии Гиббса. Эта конкуренция между стремлением системы к низшей тепловой энергии и ее приближением к высшей энтропии лежит в основе образования и устойчивости всех фаз вещества в любых условиях.

ВСЕ САМОПРОИЗВОЛЬНО ПРОТЕКАЮЩИЕ ПРОЦЕССЫ

сопровождаются уменьшением значения

ИЗОБАРНО-ИЗОТЕРМИЧЕСКОГО ПОТЕНЦИАЛА.

По аналогии с энтальпией изменение энергии Гиббса при образовании 1 моль сложного вещества из простых веществ называют энергией Гиббса образования ΔGобр. Для стандартных условий – стандартная энергия Гиббса образования ΔG⁰обр.

Связь изобарно-изотермического потенциала

с константой равновесия химической реакции.

Дифференцирование уравнения ΔG = ΔН – ТΔS приводит нас к виду

dG = VdP – SdT, которое при Т = const превращается в

dG = VdP.

Согласно уравнению Менделеева-Клапейрона V=RT/P, поэтому

dG = RT dP/P.

Интегрирование последнего уравнения при постоянной температуре приводит к выражению

ΔG = ΔG⁰ + RTlnP, где

ΔG⁰ – постоянная при данной температуре величина стандартной свободной энергии, R – универсальная газовая постоянная, Т – температура, Р – давление.

Пусть протекает обратимый процесс (реакция) аА_(г) ↔ bВ_(г)в идеальном газе.Можно записать:

Для А ΔG_а = ΔG⁰_а + аRTlnP_а

Для В ΔG_в = ΔG⁰_в + вRTlnP_в

Изменение свободной энергии в рассматриваемой реакции определяется уравнением ΔGр = ΔG_в - ΔG_а = ΔG⁰_в + вRTlnP_в – (ΔG⁰_а + аRTlnP_а). Решение этого уравнения приводит нас к уравнению

ΔGр = ΔG⁰р + RTln(Р_В)^в/(Р_А)^а,

Которое описывает изменение свободной энергии, происходящее в результате превращения газообразного реагента, находящегося при определенном давлении в газообразный продукт, находящийся при некотором ином давлении. Для состояния равновесия ΔG=0, тогда

0 = ΔG⁰р + RTln(Р_В)^в/(Р_А)^а

ΔG⁰р = - RTln(Р_В)^в/(Р_А)^а, где Р_В^в/Р_А^а = К и называется константой равновесия реакции (при условии, что Р_В и Р_А соответствуют равновесным условиям).

Для более сложной реакции aA + bB → cC + dD можно записать

ΔG⁰р = - RTln [Р_С^сР_D^d/P_A^aP_B^b].

Полученное соотношение между изменением свободной энергии и константой равновесия применимо к реакциям, протекающим не только в газовой фазе, но и в разбавленных растворах. С помощью данного уравнения можно вычислять значение К для реакции, протекающей при известной температуре Т, если известно ΔG⁰р.

Одно из наиболее важных применений термодинамики – определение изменения энтальпии, энтропии и энергии Гиббса, которыми сопровождаются химические реакции. Изменение энтальпии происходит во всех случаях, когда разрываются одни химические связи и образуются другие. Сведения об изменении энтальпии позволяют судить о природе химической реакции, поскольку основные изменения энергии, которыми сопровождается реакция, связаны с перестройкой химических связей.

Применение термодинамических функций в термохимических расчетах основано на законе Гесса:

"Тепловые эффекты химических реакций, протекающих при постоянном объёме или постоянном давлении, зависят только от природы и состояния исходных веществ и не зависят от промежуточных реакций (промежуточных, переходных состояний)".Например, рассмотримпревращение исходных реагентов в продукты через две возможные стадии – образования промежуточного продукта А и промежуточного продукта Б:

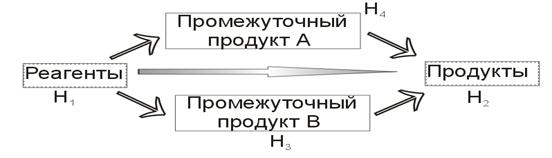
Из состояния Н₁ в состояние Н₂ можно перейти разными путями:

Н₂ – Н₁ = (Н₄ – Н₁) + (Н₂ – Н₄) = (Н₃ – Н₁) + (Н₂ – Н₃). При этом результирующее изменение энтальпии системы все равно будет равно Н₂ – Н₁.

ΔН3

ΔН2

СО

Например,

С + О₂ = СO₂ + Q₁ | Δ Н₁

С+ 1/2О₂=СО+Q₂| ΔН₂

С

СО2

СО+ 1/2 О₂ =СO₂ +Qз | ΔН_З

	ΔН1

ΔН₁ = ΔН₂ + ΔН₃

Аналогичным образом для химических процессов можно рассчитать и изменения энтропии и энергии Гиббса.

1. Расчет изменения энтальпии при химической реакции позволяет определять знак и величину теплового эффекта реакции:

Fe₂O₃ кр+ 2Al = Al₂O₃ кр+ 2 Fe

по справочнику находим стандартные значения энтальпий для реагентов и продуктов:

DН²⁹⁸обр (Fe₂O₃ кр) = -822,2 кДж/моль

DН²⁹⁸обр (Al₂O₃ кр) = -1676 кДж/моль

DН²⁹⁸обр (Al и Fe) = 0.

DН²⁹⁸ р = 1· (-1676) - 1· (-822,2) = - 853,8 кДж.

Т. о. реакция будет идти с выделением тепла. При низких температурах знак изменения энтальпии реакции может служить для ориентировочного определения возможного направления реакции.

Аналогичным образом можно рассчитать изменения в реакции энтропии и энергии Гиббса:

DG²⁹⁸обр (Fe₂O₃ кр) = - 740,3 кДж/моль

DG²⁹⁸обр (Al₂O₃ кр) = - 1582 кДж/моль

DG²⁹⁸р = 1· (-1582) - 1· (-740,3) = - 831,7 кДж.

Полученное отрицательное значения энергии Гиббса подтверждает вывод, сделанный на основе оценки изменения энтальпии реакции о возможном ее самопроизвольном протекании. Близость значений изменения энтальпии реакции и энергии Гиббса обусловлена тем, что при протекании данной реакции не меняется агрегатное состояние веществ, и следовательно, энтропия изменяется незначительно. Если бы продукты реакции переходили в газообразное состояние, то энтропия в реакции менялась бы существенно и значения энтальпии реакции и энергии Гиббса также сильно различались.

Кроме того, не производя расчетов можно оценить знак изменения энтропии в химическом процессе. Пример:

N_{2 (г)} + 3H_2(г) = 2NH_3(г)

1 молекула + 3 молекулы → 2 молекулы

S₁ > S₂ 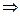ΔS < 0

NH_3(г) + HCl(г) = NH₄Cl (кр)

1 молекула + 1 молекула → 1 молекула

S₁ > S₂ ΔS < 0.

Литература_.

1. БСЭ. М.: " Сов. энциклопед.", 1978, т.30. С. 403 .

2. Очерки изъ Естественныхъ наукъ.Лекции Дж. Тиндаля.С-Петербургъ,1876. С. 160 - 170 .

3. Эткинс П. Физическая химия. М.: Мир, 1980, т.1. С. 81 - 83 .

4. Соловьёв Ю.И. Герман Иванович Гесс. Изд. АН СССР, 1962 .

5. Карапетьянц М.Х. Химическая термодинамика, 1975. С.584 .

6. У. Слейбо, Т. Персонс. Общая химия. М.: Мир. 1979. 550с.

7. Фролов В.В. Химия: Учеб. пособие для вузов. М.: Высш. школа. 1979. 559с.

8. Азимов А. Краткая история химии. М.: Мир, 1983. С. 187 .

9. Джуа М. История химии. М.: Мир, 1975. С. 407.