Примеры решения типовых задач. Пример 1Расчет концентрации комплексообразователя в растворе

Пример 1Расчет концентрации комплексообразователя в растворе

комплексного соединения, содержащем избыток лиганда.

Вычислите концентрацию иона цинка в растворе тетрацианоцинката натрия с концентрацией 0,3 моль/л при избытке цианид-ионов, равном 0,01 моль/л.

Решение. Ионы цинка в свободном виде в растворе могут находится только при полной диссоциации комплекса:

Диссоциация по внешней координационной сфере протекает практически полностью:

Na₂[Zn(CN)₄] ® 2Na⁺ + [Zn(CN)₄]^2-

Диссоциация комплексной частицы по внутренней координационной сфере:

[Zn(CN)₄]^2- Û Zn²⁺ + 4CN^-

Запишем для этого процесса выражение константы химического равновесия, она равна константе нестойкости[Zn(CN)₄]² :

с( Zn²⁺)c⁴(CN^-)

К_{н =} ¾¾¾¾¾¾¾¾

с(компл.иона)

Преобразуем это выражение относительно К_н:

К_н с(компл.иона)

с( Zn²⁺)= ¾¾¾¾¾¾¾

c⁴(CN^-)

где К_н - табличная величина (см. справочник табл. ); К_н = 2,4×10^-20.

Поскольку концентрация цианид-ионов, образующихся в результате диссоциации комплексного иона, значительно меньше концентрации введенного избытка, можно считать, что с(CN^-) = 0,01 моль/л , т.е. концентрацией цианид-ионов, образующихся в результате диссоциации комплексного иона пренебрегаем. Таким образом, подстановка в полученное выражение дает следующий результат:

2,40×10^-20× 0,3

с(Zn²⁺) = ¾¾¾¾¾¾ = 7,2 × 10^-13 моль/л

(0,01)⁴

Ответ: 7,2 × 10^-13 моль/л.

Пример 2Расчет массы комплексообразователя в растворе комплексного

соединения известного объема, содержащем избыток лиганда.

Вычислите массу серебра, содержащегося в виде ионов в растворе хлорида диамминсеребра(I) с концентрацией 0,03 моль/л объемом 750 мл. Раствор содержит аммиак, концентрация которого равна 0,1 моль/л.

Решение. Ионы серебра в свободном виде в растворе могут находиться при полной диссоциации комплекса:

[Ag(NH₃)₂]⁺ Û Ag⁺ + 2NH₃

Запишем для этого процесса константу химического равновесия, она будет равна константе нестойкости диамминсеребра:

с(Ag⁺)с²(NН₃)

К_н = ¾¾¾¾¾¾¾¾¾

с(компл.иона)

В данном выражении используют значение с(NH₃) = 0,1 моль/л, т.к. концентрация аммиака, образующегося при диссоциации комплексного иона, значительно меньше этой величины и ,следовательно, ею можно пренебречь.

Отсюда,

К_н с(компл.иона) 5,89 ×10 ^–8× 0,3

с(Ag⁺) = ¾¾¾¾¾¾¾¾ = ¾¾¾¾¾¾¾ = 1,77 ×10 ^–6 моль/л

с²(NН₃) 0,1²

m(Ag⁺) = M(Ag)Vc(Ag⁺) = 108 г/моль × 0,75 л ×1,77× 10^-6 моль/л = 1,43 ×10^-4 г

Ответ: 1,43 × 10^-4 г.

Пример 3Расчет концентрации иона металла

в растворе после введения избытка лиганда.

Во сколько раз изменится концентрация иона железа(Ш) при введении в раствор хлорида железа(Ш) с концентрацией 0,5 моль/л тартрат-ионов до концентрации 0,05 моль/л?

Решение. Концентрация ионов Fe³⁺ в исходном растворе равна молярной концентрации (0,5 моль/л). После введения татрат -ионов ионы железа связываются в комплекс. Молярная концентрация образовавшегося комплексного иона будет равна молярной концентрации исходного раствора хлорида железа, т.к. тартрат-ион был введен в избытке, а стехиометрическое соотношение между ионом железа(Ш) и его комплексом равно 1:1. Обозначим двухзарядный анион винной кислоты Tartr^2-. Концентрация ионов железа(Ш) будет определяться теперь нестойкостью образовавшегося дитартратного комплекса:

[Fe(Tartr)₂]^- Û Fe³⁺ + 2 Tartr^2-

Аналогично решению предыдущей задачи:

К_н с(компл.иона) 1,38×10^-12× 0,5

c(Fe³⁺) = ¾¾¾¾¾¾¾¾¾ = ¾¾¾¾¾¾ = 2,76× 10^-10 моль/л

с²(Tartr^2-) (0,05)²

0,5

Ответ: отношение концентраций ¾¾¾¾¾ = 1,8 ×10⁹ т.е. концентрация ионов железа уменьшится в 1,8 млрд. раз.

2,76 ×10^-10

Пример 4Расчет концентрации и массы иона металла

в растворе после введения избытка лиганда.

К хлориду кальция массой 1,11 г добавили аммиачный буферный раствор и раствор объемом 1 л этилендиаминтетраацетата натрия с концентрацией 0,05 моль/л. Вычислите массу кальция, содержащегося в виде ионов в таком растворе. Вычислите, какая часть ионов кальция находится в свободном состоянии, а какая - в связанном виде.

Решение. Вычислим количество веществ хлорида кальция и этилендиаминтетраацетата натрия:

m 1,11 г

n(CаСl₂) = ¾¾ = ¾¾¾¾¾ = 0,01 моль

M111г/моль

n(Nа₂Н₂ЭДТА) = сV = 0,05× 1 = 0,05 моль

СаСl₂ + Nа₂Н₂ЭДТА = СаН₂ЭДТА + 2NаСl

Хлорид кальция вступает в реакцию полностью, поэтому

n(СаН₂ЭДТА) = n(СаСl₂) = 0,01 моль

n(NаН₂ЭДТА)_ост =0,05 – 0,01 моль = 0,04 моль

соответственно,

с(NаН₂ЭДТА) ₌ 0,04 моль/л.

Ионы кальция в свободном виде в растворе могут находиться только при полной диссоциации комплекса:

СаН₂ЭДТА Û Ca²⁺ + ЭДТА^4- + 2Н⁺

Применяемый аммиачный буфер нейтрализует образовавшиеся в результате реакции ионы водорода.

Концентрация ионов кальция (свободная часть ионов кальция) определяется из выражения константы нестойкости :

К_нс(компл.иона)

с(Са²⁺)_своб = ¾¾¾¾¾¾¾¾

с(ЭДТА^4-)

Подставив в это выражение значения К_н (СаЭДТА^2-)(табл. ), концентрации комплексного иона и лиганда, вычислим концентрацию свободных ионов кальция:

2,57× 10^-11×0,01

с(Са²⁺)_своб = ¾¾¾¾¾¾¾ = 6,43× 10^-12 моль/л

0,04

m(Са²⁺) = cMV = 6,43 ×10^-12 моль/л ×40 г ×1л = 2,57×10^-10 г

Концентрация ионов кальция в связанном виде определяется разностью концентраций комплексного иона и свободных ионов кальция:

с(Са²⁺)_связ = 0,01 - 6,43 ×10^-11 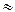0,01 моль/л

с(Са²⁺) _связ 0,01 моль/л

¾¾¾¾ = ¾¾¾¾¾¾¾¾¾ = 1,56×10⁹

с(Са²⁺) _своб 6,43× 10^-12 моль/л

Ответ: масса ионов кальция равна 2,57×10^-10 г; на одну часть свободных ионов приходится 1,56×10⁹ частей связанных.

Пример 5 . Определение направления смещения лигандообменных процессов.

В каком направлении сместится равновесие реакции, если смешать реагенты в указанных концентрациях:

Тетраамминмедь(П)-ион Û медь(П)-ион + аммиак

0,1 моль/л 0,0000001 моль/л 2 моль/л

Решение: Для ответа на вопрос задачи воспользуемся уравнением изотермы химической реакции:

DG = - RTlnK_н + RTlnП_с.

Вычислим П_с и сравним его с табличным значением константы, которое найдем в табл.

Поскольку записанный процесс представляет собой полную диссоциацию комплексного иона, П_с надо сравнить с константой нестойкости [Cu(NH₃)₄]²⁺.

В случае П_с<К_н пойдет прямой процесс, т.е. положение равновесия сместится вправо; в случае П_с>К_н - влево.

с(Сu ²⁺)с⁴(NH₃) 0,0000001×2⁴

П_с = ¾¾¾¾¾¾¾¾ = ¾¾¾¾¾¾¾¾ = 1,60×10 ^-5

с(компл.иона) 0,1

Табличное значение константы нестойкости иона равно 9,33 ×10^-13.

Ответ: поскольку П_с> К_н, положение равновесия сместится влево.

Пример 6 Сравнение концентраций катионов металлов в растворах

комплексных соединений в отсутствие избытка лиганда.

Во сколько раз концентрация ионов кальция будет больше концентрации ионов марганца в растворах их комплексов с глицином одинаковых концентраций?

Решение. Ионы кальция в свободном виде в растворе могут находиться при полной диссоциации комплекса:

[Са-Gly]⁺ Û Са²⁺ + Gly ^–

где Gly = глицин

Запишем для этого процесса константу химического равновесия, она будет равна константе нестойкости :

с(Са²⁺)с(Gly ^–-)

К_н = ¾¾¾¾¾¾¾

с(Ca-Gly )

Обозначим за х концентрацию ионов кальция в растворе, тогда

с(Са²⁺) = с(Gly ^–) = х;

х²

К_н = ¾¾¾¾¾ ;

с(Ca-Gly ^–)

Откуда

¾¾¾¾¾¾

х = с(Са²⁺) = Ö К_н с(Ca-Gly)

Аналогично рассуждая, выразим концентрацию ионов марганца:

¾¾¾¾¾¾

с(Мn²⁺) = Ö К_н с(Mn-Gly)

Учитывая, что концентрации комплексов одинаковы, выразим и вычислим отношение концентраций ионов кальция и марганца:

¾¾¾¾¾¾ ¾¾¾¾¾¾¾¾¾ ¾¾¾¾ ¾¾¾¾¾

с(Са²⁺) Ö К_н с(Ca-Gly) К_н (Ca-Gly)с(Ca-Gly ) К_н(Ca-Gly) 4,17×10^-2

¾¾¾ = ¾¾¾¾¾¾¾ = Ö ¾¾¾¾¾¾¾¾¾ = Ö ¾¾¾ = Ö ¾¾¾¾¾ = 10,72

с(Мn²⁺) Ö К_н с(Mn-Gly) К_н (Mn-Gly) с(Mn-Gly) К_н(Mn-Gly) 3,63×10^-4

Ответ: концентрация ионов кальция больше в 11 раз концентрации ионов марганца в растворах их комплексов с глицином.

Пример 7Расчет константы нестойкости с использованием стандартного

изменения энергии Гиббса совмещенного лигандообменного процесса.

Реакция замещения Са²⁺ на Ве²⁺ в составе комплекса с ЭДТА ^4- характеризуется DG° = 11,8 кДж/моль.

Вычислите константу нестойкости комплекса ВеЭДТА^2-.

Решение. Запишем уравнение замещения Са²⁺ на Ве²⁺ в составе комплекса с ЭДТА ^4-:

СаЭДТА^2- + Ве²⁺Û ВеЭДТА^2- + Са²⁺

Константы совмещенного лигандообменного процесса равна отношению константы нестойкости комплексного соединения, стоящего в левой части уравнения, на константу нестойкости комплексного соединения вещества, стоящего в правой части уравнения. Таким образом:

К_н(СаЭДТА^2-)

К = ¾¾¾¾¾¾¾ ;

К_н(ВеЭДТА^2-)

Величины DG° и К связаны между собой соотношением:

DG⁰ = - RTlnК.

Вычислм константу равновесия:

К = е ^-DG0/RT

К = е^{-11800/8,31×298} = 8,52×10^-3

Выразим и вычислим К_н(ВеЭДТА^2-):

К_н(СаЭДТА^2-) 2,57×10^-11

К_н(ВеЭДТА^2-) = ¾¾¾¾¾¾ = ¾¾¾¾¾¾¾ = 3,02×10^-9

К 8,52×10^-3

Ответ: 3,02×10^-9