Решение задачи с помощью MS Excel. 1. Отвести ячейки A3 и ВЗ под значения переменных х1 и х2 (рис

1. Отвести ячейки A3 и ВЗ под значения переменных х1 и х2 (рис. 1).

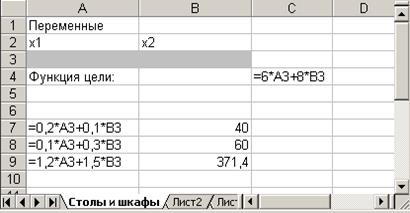
Рис. 1. Диапазоны, отведенные под переменные, целевую функцию и ограничения

2. В ячейку С4 ввести функцию цели: =6*АЗ+8*ВЗ, в ячейки А7:А9 ввести левые части ограничений:

=0,2*А3+0,1*ВЗ

=0,1*А3+0,3*ВЗ

= 1,2*АЗ+1,5*ВЗ,

а в ячейки В7:В9 - правые части ограничений. (рис.1).

3. Выбрать команды Сервис/Поиск решения и заполнить открывшееся диалоговое окно Поиск решения как показано на рис 2. Средство поиска решений является одной из надстроек Excel. Если в меню Сервис отсутствует команда Поиск решения, то для ее установки необходимо выполнить команду Сервис/ Надстройки/ Поиск решения.

Для ввода ограничений нажмите кнопку Добавить.

Внимание! В диалоговом окне Параметры поиска решениянеобходимо установить флажок Линейная модель (Рис.3.).

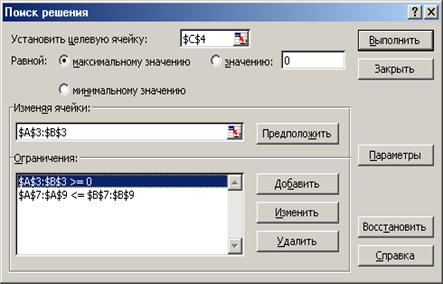
Рис. 2. Диалоговое окно Поиск решения задачи о максимизации прибыли на фабрике

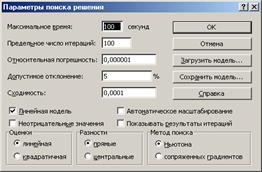
Рис 3. Параметры поиска решения

4. После нажатия кнопки Выполнить открывается окно Результаты поиска решения, которое сообщает, что решение найдено (рис. 4).

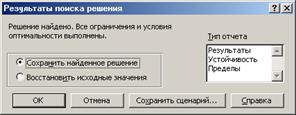
Рис. 4. Результаты поиска решения

5. Результаты расчета задачи представлены на рис. 5, из которого видно, что оптимальным является производство 102 столов и 166 шкафов Этот объем производства принесет фабрике 1940 руб. прибыли.

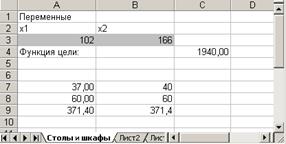
Рис. 5. Результаты расчета

Индивидуальное задание

1. Построить математическую модель задачи, согласно Вашему варианту.

2. Решить задачу с помощью средства MS Exсel Поиск решения.

Задание 2 «Транспортная задача»

Краткие теоретические сведения

Транспортная задача — задача о поиске оптимального распределения поставок однородного товара от поставщиков к потребителям при известных затратах на перевозку (тарифах) между пунктами отправления и назначения. Задача записывается в виде прямоугольных таблиц следующего вида:

Таблица 2

Поставки однородного товара от поставщиков к потребителям

	Потребитель B1, потребность 20 кг	Потребитель B2, потребность 30 кг	Потребитель B3, потребность 30 кг	Потребитель B4, потребность 10 кг
Поставщик A1, запас 30 кг	С11=2 руб./кг	С12=3 руб./кг	С13=2 руб./кг	С14=4 руб./кг
Поставщик A2, запас 40 кг	С21=3 руб./кг	С22=2 руб./кг	С23=5 руб./кг	С24=1 руб./кг
Поставщик A3, запас 20 кг	С31=4 руб./кг	С32=3 руб./кг	С33=2 руб./кг	С34=6 руб./кг

Цена перевозки (например, в рублях за 1 килограмм груза) C_ij записывается в ячейки таблицы на пересечении соответствующего потребителя и поставщика (цена может быть и отрицательной — в этом случае она представляет собой прибыль). Неизвестной (искомой) величиной в задаче являются такие объемы перевозки x_ij от поставщиков к потребителям, чтобы минимизировать общие затраты на транспортировку. В табличной записи цены отделяют от объемов перевозки косой чертой или квадратным уголком, в этой статье из соображений лучшей доходчивости они подписаны. При решении транспортной задачи единственными необходимыми арифметическими действиями являются сложение и вычитание. Транспортную задачу можно решать также в Excel.

Контрольный пример

Фирма имеет 4 фабрики и 5 центров распределения ее товаров. Фабрики фирмы располагаются в Денвере, Бостоне, Новом Орлеане и Далласе с производственными возможностями 200, 150, 225 и 175 единиц продукции ежедневно, соответственно. Центры распределения товаров фирмы располагаются в Лос-Анджелесе, Далласе, Сент-Луисе, Вашингтоне и Атланте с потребностями в 100, 200, 50, 250 и 150 единиц продукции ежедневно, соответственно. Хранение на фабрике единицы продукции, не поставленной в центр распределения, обходится в $0,75 в день, а штраф за просроченную поставку единицы продукции, заказанной потребителем в центре распределения, но там не находящейся, равен $2,5 в день Стоимость перевозки единицы продукции с фабрик в пункты распределения приведена в таблице 3:

Таблица 3

Транспортные расходы

		Лос-Анджелес	Даллас	Сен-Луис	Вашин- гтон	Атланта
	Денвер	1,50	2,00	1,75	2,25	2,25
	Бостон	2,50	2,00	1,75	1,00	1,50
	Новый Орлеан	2,00	1,50	1,50	1,75	1,75
	Даллас	2,00	0,50	1,75	1,75	1,75

Необходимо так спланировать перевозки, чтобы минимизировать суммарные транспортные расходы.

Поскольку данная модель сбалансирована (суммарный объем произведенной продукции равен суммарному объему потребностей в ней), то в этой модели не надо учитывать издержки, связанные как со складированием, так и с недопоставками продукции. В противном случае в модель нужно было бы ввести:

· в случае перепроизводства – фиктивный пункт распределения, стоимость перевозок единицы продукции в который полагается равной стоимости складирования, а объемы перевозок объемам складирования излишков продукции на фабриках;

· в случае дефицита – фиктивную фабрику, стоимость перевозок единицы продукции с которой полагается равной стоимости штрафов за недопоставку продукции, а объемы перевозок – объемам недопоставок продукции в пункты распределения.

Для решения данной задачи построим ее математическую модель.

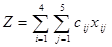
Неизвестными в данной задаче являются объемы перевозок. Пусть x_ij - объем перевозок с i-ой фабрики в j-й центр распределения. Функция цели - это суммарные транспортные расходы, т. е. где с_ij – стоимость перевозки единицы продукции с i-и фабрики j-й центр распределения.

Неизвестные в данной задаче должны удовлетворять следующим ограничениям:

· Объемы перевозок не могут быть отрицательными.

· Так как модель сбалансирована, то вся продукция должна быть вывезена с фабрик, а потребности всех центров распределения должны быть полностью удовлетворены.

В результате имеем следующую модель: Минимизировать:

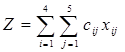
при ограничениях:

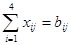, j Î [1,5]

x_ij ³ 0, iÎ [1,4], jÎ [1,5

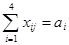, iÎ [1,4],

где a_ij - объем производства на i-й фабрике, b_j — спрос в j-м центре распределения.