Злектрокапиллярные явления на ртути и твердых металлах
В основе электрокапиллярных явлений лежит зависимость обратимой поверхностной работы (поверхностного натяжения) от потенциала электрода, которая может быть получена из уравнения Гиббса (см. разд. 1). Для вывода этой зависимости рассмотрим границу ртутный электрод (Hg) — раствор (Р), содержащей i компонентов. Потенциал ртутного электрода можно изменять, внося в раствор различные количества ионов ртути Hg22+. Зависимость Гальвани-потенциала на этой границе от активности ионов ртути подчиняется уравнению Нернста:
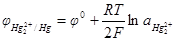
Выделим в уравнении Гиббса тот компонент, ионы которого могут переходить через границу раздела металл — раствор;
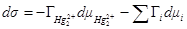
Из выражений для химического н Гальвани-потенциалов получаем:
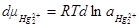
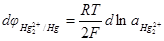
Значение адсорбции 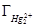 можно определить следующим образом. Увеличим поверхность раздела ртуть — раствор на 1 м2. При этом для того чтобы сохранилась постоянной плотность заряда на электроде, некоторое количество ионов ртути должно перейти из раствора на металл или в противоположном направлении. Следовательно
можно определить следующим образом. Увеличим поверхность раздела ртуть — раствор на 1 м2. При этом для того чтобы сохранилась постоянной плотность заряда на электроде, некоторое количество ионов ртути должно перейти из раствора на металл или в противоположном направлении. Следовательно
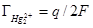
Подставляя полученные выражения в уравнение для dσ, окончательно имеем:
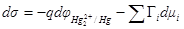
Это выражение называется основным уравнением электрокапиллярности.
Изменение Гальвани-потенциала на границе ртуть — раствор свяжем с изменением потенциала электрода в относительной шкале. Представим правильно разомкнутую электрохимическую систему, состоящую из металлического электрода М (в общем случае электрод сравнения) и ртутного Hg в одном и том же растворе (Р). Напряжение этой системы равно:
E = φHg P + φP M + φM Hg
При изменении состава раствора изменится напряжение, следовательно
dE = dφHg P + dφP M и dφHg P = dE – dφP M
(dφM Hg = 0, поскольку Гальвани-потенциал на границе металл —
ртуть не зависит от состава раствора). Подставим в последнее уравнение выражение для изменения Гальвани-потенциала на границе металл — раствор:
dφHg P = dE + 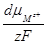
(так как 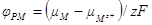 , то
, то 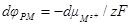 ибо
ибо  = const). Тогда основное уравнение электрокапиллярности за-
= const). Тогда основное уравнение электрокапиллярности за-
писываем в виде:
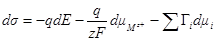
Это уравнение называется точным уравнением электрокапилляр-ности.
Если электрод сравнения находится в том же растворе, что и ртутный, то при изменении концентрации раствора изменяется его равновесный потенциал и 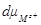 ≠ 0. Для электрода сравнения (например, хлорсеребряного или каломельного), обратимого относительно аниона электролита
≠ 0. Для электрода сравнения (например, хлорсеребряного или каломельного), обратимого относительно аниона электролита
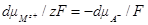
поскольку валентность аниона электрода сравнения равна единице. При Е = const dE = 0 и тогда из точного уравнения электрокапиллярности имеем:
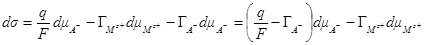
Так как 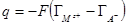 , то
, то
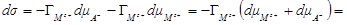
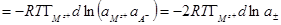
и
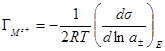
Таким образом, при использовании электрода сравнения, обратимого относительно аниона, из экспериментально полученных зависимостей снижения поверхностного натяжения от активности электролита при постоянном напряжении Е определяют адсорбцию катиона.
Аналогичным способом получают выражение для адсорбции анионов, если в качестве электрода сравнения выбран электрод, обратимый относительно катиона электролита:
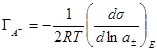
Если зависимость поверхностного натяжения от потенциала получена в растворе постоянного состава (dμ = 0), то из уравне
ния электрокапиллярности непосредственно следует первое уравнение Липпмана:
dσ = – qdE
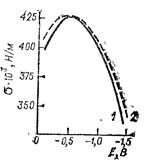
Рис. 7.1. Электрокапиллярные кривые ртутного электрода в растворе NaF.
Концентрация NaF, кмоль/м3; 1 — 0,9; 2 — 0,01.
Из уравнения электрокапиллярности, если предположить 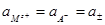 , также
, также
следует, что в растворе 1—1-валентного поверхностно-неактивного электролита
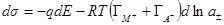
и при q = 0 имеем 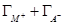 = 0 и σ = const.
= 0 и σ = const.
Из условия электронейтральности
q = – F( 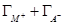 ) = 0
) = 0
следовательно, при потенциале нулевого заряда 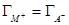 = 0.
= 0.
Электрокапиллярные кривые в растворах поверхностно-неактивных электролитов, таких, как NaF, Na2SO4, NaHCO3, Na2HPO4, KF, NaOH, хорошо друг с другом совпадают. Зависимость поверхностного натяжения от потенциала при разных концентрациях NaF приведена на рис. 7.1. Максимальное поверхностное натяжение на ртутном электроде наблюдается при потенциале –0,473 В относительно нормального каломельного электрода (н.к.э.) или –0,193 В по нормальному водородному электроду, (н.в.э.). При увеличении концентрации электролита (0,9 кмоль/м3) вправо и влево от максимума наблюдается снижение поверхностного натяжения. Смещение потенциала при σ = const может быть найдено из уравнения электрокапиллярности:
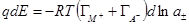
Например, при высоких отрицательных зарядах поверхности 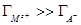 и
и  . Исходя из этого условия, получим:
. Исходя из этого условия, получим:
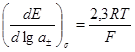
Из этого уравнения следует, что при изменении активности электролита в 10 раз отрицательная ветвь электрокапиллярной кривой в растворе 1 — 1-валентного электролита при 25 °С сдвигается на 59 мВ в положительную сторону. Когда Е = const уравнение электрокапиллярности позволяет определить сумму адсорбций катиона и аниона
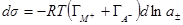
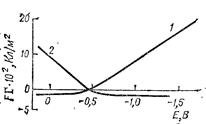
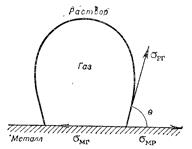
Рис. 7.2. Зависимость адсорбции катионов (1) и анионов (2) от потенциала ртутного электрода в растворе поверхностнонеактивного электролита.
Рис. 7.3. Равновесие сил на границе металл — газ — раствор.
откуда
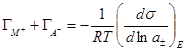
Из точного уравнения электрокапиллярности не представляет экспериментальных трудностей раздельное определение 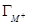 или
или 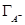 . Зависимость адсорбции катионов и анионов от потенциала для поверхностно-неактивного электролита приведена на рис. 7.2.
. Зависимость адсорбции катионов и анионов от потенциала для поверхностно-неактивного электролита приведена на рис. 7.2.
При высоких зарядах поверхности наблюдается увеличение адсорбции либо катионов (при q < 0), либо анионов (при q > > 0), а при Е = Ен. з (где Ен. з — потенциал нулевого заряда) q = 0 и 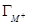 =
= 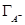 = 0.
= 0.
Адсорбция имеет отрицательное значение при заряде иона, одинаковом с зарядом поверхности. Все эти явления связаны с чисто электростатическим характером адсорбции.
Электрокапиллярные явления, т. е. зависимость поверхностного натяжения от потенциала, наблюдаются как на жидких, так и на твердых металлах. Для последних изменение поверхностного натяжения может быть определено косвенными методами, например по измерению угла смачивания. Поле двойного электрического слоя оказывает существенное влияние на равновесие в системе газ — жидкость — твердое тело. Если на поверхности электрода, горизонтально расположенного в каком-либо электролите, находится пузырек газа (рис. 7.3), то на границах раздела фаз на него действуют силы, пропорциональные поверхностному натяжению, которые определяют значение краевого угла смачивания 9. Из условия равновесия сил, показанных на рис. 7.3, имеем
σМГ = σМР + σРГ cos θ
(индексы М, Г, Р обозначают соответственно металл, газ и раствор), откуда
cos θ = (σМГ – σМР)/σРГ
При изменении потенциала электрода в первом приближении можно считать, что изменяется лишь пограничное натяжение на границе металл — раствор, а σМГ и σРГ — величины постоянные. В этом случае сдвиг потенциала электрода относительно потенциала нулевого заряда в положительную или отрицательную сторону вызывает снижение σМР, что приводит к росту cos θ и уменьшению краевого угла смачивания θ. Зависимость краевого угла смачивания от потенциала получается совершенно аналогичной электрокапиллярной кривой.
Изменение поверхностного натяжения твердых металлов в за-висимости от потенциала электрода можно определить также методом поверхностной твердости, разработанным П. А. Ребиндером и Е. К- Венстрем. Метод основан на измерении поверхностной твердости металла без его разрушения. Так как поверхностное натяжение зависит от потенциала и определяет поверхностную твердость, то последняя должна изменяться по закону электрокапиллярной кривой. Результаты, полученные этим методом, позволили качественно показать, что основные закономерности, справедливые для жидких электродов, выполняются и на твердых электродах.
Для установления зависимости σ — Е А. Я. Гохштейн предложил метод измерения эстанса, т. е. производной поверхностного натяжения (вектор) от плотности заряда. Эстанс связан с изменением потенциала и проходит через нуль при потенциале нулевого заряда. Метод основан на том, что на исследуемый электрод подается напряжение и накладывается переменное напряжение малой амплитуды. При изменении плотности заряда на электроде изменяется σ, это изменение минимально при потенциале нулевого заряда. В результате изменения поверхностного натяжения изменяется форма электрода и его размеры. Колебания формы и размеров преобразуются пьезоэлектрическим датчиком в электрические сигналы, усиливаются и регистрируются в виде зависимости эстанса от потенциала.
