Вводится понятие относительной диэлектрической проницаемости

ДИЭЛЕКТРИЧЕСКИЕ МАТЕРИАЛЫ

Основные понятия и общие сведения о диэлектриках

Условно к диэлектрикам относят материалы с удельным электрическим сопротивлением 𝜌 > 10⁸ Ом・м. С точки зрения зонной теории, диэлектриками условно называют вещества с шириной запрещенной зоны превышающей 3-8 эВ.

Термин «диэлектрики» впервые ввел английский физик ФАРАДЕЙ для обозначения веществ, пропускающих через себя электрическое поле.

Характерными особенностями любого диэлектрика являются:

- поляризация в электрическом поле;

- высокое удельное сопротивление;

- незначительное рассеяние энергии электрического поля;

- высокая электрическая прочность т.е. способность противостоять сильным электрическим полям

Свойства диэлектриков могут зависеть от температуры и влажности окружающей среды, от условий теплоотвода, частоты и равномерности электрического поля, степени однородности самого диэлектрика, его агрегатного состояния и других факторов.

Все диэлектрики обладают изоляционными свойствами.

Проводимость реальных Диэлектриков в 10¹³ -10²³ раз меньше проводимости проводниковых материалов. Такой широкий диапазон проводимости обусловлен различием природы их химических связей.

РАЗЛИЧАЮТ ДВА КЛАССА ДИЭЛЛЕКТРИКОВ

∙ Линейные диэлектрики (имеющие линейную зависимость заряда конденсатора от напряжения).

К этому классу диэлектриков относятся:

– Неполярные диэлектрики — газы, жидкости и твердые вещества, обладающие в основном только электронной поляризацией. К ним относятся водород, бензол, сера, полиэтилен.

– Полярные диэлектрики — органические жидкие, полужидкие и твердые вещества, имеющие одновременно электронную и дипольно-релаксационную поляризации. К ним относятся кремнийорганические соединения, капрон, фенолформальдегидные смолы.

– Ионные диэлектрики. В этой группе целесообразно выделить две подгруппы материалов:

* диэлектрики с ионной и электронной поляризациями (кварц, слюда, корунд, TiO2);

* диэлектрики с ионной, электронной и релаксационной поляризацией (неорганические стекла, керамика).

∙ Нелинейные диэлектрики (зависимость заряда от напряжения принимает форму петли гистерезиса).

К этому классу диэлектриков относятся только сегнетоэлектрики (вещества, обладающие спонтанной поляризацией)

Поляризация диэлектриков.

При приложении электрического поля к диэлектрику, не происходит переноса свободных носителей заряда, т. к. их концентрация ничтожно мала. Однако при этом происходит смещение связанных зарядов, вызывающее появление поляризованного состояния (рис. 3.1).

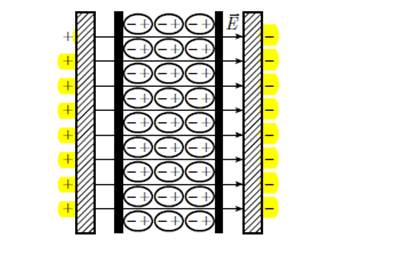
Рис. 3.1. Поляризация бесконечного плоского диэлектрика

Поляризациейназывают состояние диэлектрика, характеризующееся наличием электрического момента у любого элемента его объема.

Различают поляризацию, возникающую под действием внешнего электрического поля, и спонтанную(самопроизвольную), существующую в отсутствие поля. В некоторых случаях поляризация диэлектриков появляется под действием механических напряжений.

По электрическим свойствам молекулы диэлектрика эквивалентны электрическим диполям, которые характеризуются дипольным моментом p. Если в отсутствие внешнего электрического поля расстояние между центрами тяжести положительных и отрицательных зарядов 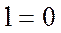, то диэлектрики называются неполярными. Если в тех же условиях 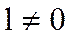, то диэлектрики называются полярными.

Молекулы, в которых центры положительных и отрицательных зарядов совпадают, называют неполярными. Молекулы, в которых центры противоположных по знаку зарядов не совпадают и находятся на некотором расстоянии друг от друга, называют полярными или дипольными. Примеры неполярной и полярной молекул приведены на рис. 3.2 а и б соответственно.

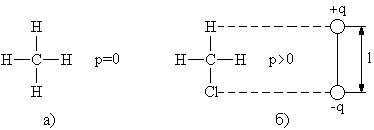
Пример: СН4 (метан) СН3Сl

Рис. 3.2 Примеры неполярной (а) и полярной (б) молекул

Дипольная молекула характеризуется дипольным моментом, который определяется произведением заряда на расстояние между центрами положительных и отрицательных зарядов:

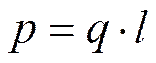(Кл*м) (3.1)

- Заряд q » 2×10^-19 Кл,

- расстояние l = (1-3) ×10^-10 м.

Поэтому обычно дипольные моменты молекул p = 5×10^-29 - 10^-30 единиц СИ.

Для неполярных диэлектриков в отсутствие внешнего поля 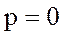. Во внешнем электрическом поле происходит деформация молекулы и возникает индуцированный дипольный электрический момент молекулы:

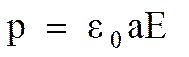, (3.2)

Где:

а – коэффициент поляризуемости (поляризуемость) молекулы или атома;

e₀ – электрическая постоянная;

Е – напряженность поля.

Поляризациейназывают состояние диэлектрика, характеризующееся тем, что дипольные электрические моменты каждого элемента объема диэлектрика отличны от нуля.

Мерой поляризации диэлектрика является вектор поляризации (поляризованность).

Поляризованностью Р называют векторную сумму дипольных моментов молекул, находящихся в единице объема:

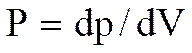[Кл/м²] (3.3)

Поляризованность (P)характеризует интенсивность поляризации диэлектрика, такого состояния вещества, при котором его элементарный объем приобретает электрический момент,

Для однородного неполярного диэлектрика, находящегося в однородном электрическом поле, ПОЛНЫЙ ЭЛЕКТРИЧЕСИЙ МОМЕНТ ОПРЕДЕЛЯЕТСЯ ФОРМУЛОЙ:

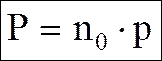, (3.4)

Где:

р – индуцированный момент одной молекулы,

n₀ – число молекул в единице объема.

Подставив (3.2) в (3.4) получаем:

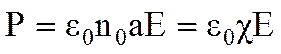, (3.5)

где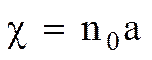

- диэлектрическая восприимчивость вещества, или поляризуемость единицы объема диэлектрика, пропорциональная объему всех молекул в 1 см³. (КСИ)

Как известно из электростатики электрическое поле характеризуется электрическим смещениемD, являющимся векторной величиной. Для поля в диэлектрике векторы смещения D, поляризации Р и напряженности электрического поля Е связаны следующим соотношением:

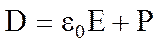(3.6)

В анизотропных кристаллических диэлектриках электрические свойства различны в разных направлениях (диэлектрическая восприимчивость является тензорной характеристикой). Поэтому в общем случае векторы Р и D не совпадают по направлению с вектором Е напряженности поля.

В изотропных диэлектриках вектор поляризации Р пропорционален напряженности поля Е и совпадает с ним по направлению. Поэтому, электрическое смещение определяется. Как

ЭЛЕКТРИЧЕСКОЕ СМЕЩЕНИЕ ОПРЕДЕЛЯЕТСЯ

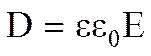, (3.7)

Где:

e - относительная диэлектрическая проницаемость, являющаяся скалярной величиной.

Вводится понятие относительной диэлектрической проницаемости

Подставив в (3.6) соотношения (3.5) и (3.7) получим связь между относительной диэлектрической проницаемостью (e) и диэлектрической восприимчивостью ( c) формулой:

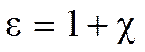(3.8)