Расчет энергетической прочности ионной решетки
В ионном кристалле ион одного знака окружает слой противоположно заряженных ионов, затем следует слой ионов того же знака и т.д. Рассмотрим ионный кристалл типа NaCl (рис. 1.4 а), в первой координационной сфере которого находятся 6 ионов противоположного знака на расстоянии R 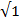 = а/2, где R - расстояние между центрами ионов, a – период кубической решетки; во второй координационной сфере находятся 12 ионов того же знака на расстоянии R
= а/2, где R - расстояние между центрами ионов, a – период кубической решетки; во второй координационной сфере находятся 12 ионов того же знака на расстоянии R 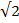 , в третьей сфере – 8 ионов противоположного типа на расстоянии R
, в третьей сфере – 8 ионов противоположного типа на расстоянии R 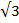 и т.д.
и т.д.
Энергия кулоновского взаимодействия центрального иона со всем его окружением будет выражаться суммой 

U = 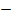
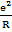 (
( 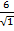
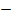
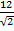 +
+ 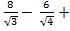
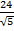 …) =
…) = 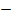 A
A 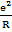 . (1.1)
. (1.1)
В сумме слагаемых, записанных в скобках, числителем являются координационные числа, знаменателем - относительные радиусы первой, второй и далее координационных сфер.
Величина А, получаемая в результате суммирования бесконечного ряда, заключенного в скобки, зависит от структуры, но не зависит от периода решетки. Она называется постоянной Маделунга в честь ученого, впервые (в 1918 г.) рассчитавшего такие суммы для наиболее важных решеток.
Постоянные Маделунга для различных структур приведены в табл. 1.2.
Энергия кулоновского взаимодействия ионов в изолированной молекуле равна 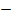
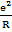 , ( т.е. А = 1). В кристалле энергия взаимодействия возрастает примерно на 75
, ( т.е. А = 1). В кристалле энергия взаимодействия возрастает примерно на 75  .
.
Если заряды ионов отличны от 1, например, для кристалла 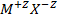 , энергия кулоновского взаимодействия равна
, энергия кулоновского взаимодействия равна
U = 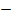 A
A 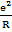 Z2 (1.2)
Z2 (1.2)
При сближении ионов помимо энергии притяжения следует учитывать энергию сил отталкивания.
Для любого типа взаимодействия атомов потенциальная энергия складывается из энергий притяжения и отталкивания – рис.1.10.
Таблица 1.2
Константы Маделунга для различных структур
| Структурный тип | К.ч. и форма полиэдра | А |
| CsCl , куб. | 8, куб | 1,7627 |
| NaCl, куб. | 6, октаэдр | 1,7476 |
| NiAs, гекс., с/а = 1,30 | 6, октаэдр и тригональная призма | 1,665 |
| ZnS, куб. | 4, тетраэдр | 1,638 |
| PtS, тетр., с/а = 1 | 4, плоский квадрат | 1,605 |
| Природа химической связи едина для всех типов кристаллов: это электростатическое взаимодействие электронов и ядер внутри и между атомами, сближенными на расстояния, когда перекрываются электронные оболочки. Для кристаллов с любым типом химической связи результирующая энергия взаимодействия может быть записана в виде обобщенной функции Ми |
U = 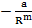 +
+ 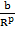 (p
(p 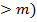 , (1.3)
, (1.3)
где первое слагаемое соответствует энергии притяжения, второе – отталкивания.
При m = 1 и р = 5 – 12 формула (1.3) соответствует сильному взаимодействию и выражает энергию в ионном кристалле; при m = 6 и р = 12 соответствует наиболее слабому взаимодействию и выражает энергию молекулярных кристаллов, в которых силами взаимодействия являются дисперсионные силы (силы Ван-дер-Ваальса).
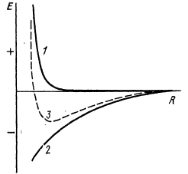
Рис.1.10. Потенциальная энергия взаимодействия для любого типа химической связи в зависимости от межатомного расстояния: 1 – отталкивания, 2 – притяжения, 3 - суммарная энергия
Энергия отталкивания может быть выражена и через экспоненциальную функцию, тогда
U = 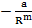 + В exp (
+ В exp ( 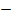
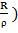 , (1.4)
, (1.4)
где 𝜌 является некоторой константой.
Для ионного кристалла с учетом формулы (1.1) выражения для энергии (1.3) и (1.4) имеют вид
U = 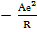 + b/Rn , (1.5)
+ b/Rn , (1.5)
U = 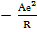 + В exp (
+ В exp ( 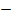
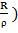 . (1.6)
. (1.6)
В состоянии равновесия энергия решетки минимальна, для равновесного межатомного расстояния R0 выполняется условие экстремума
( 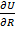 )R = Ro =
)R = Ro = 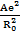
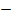
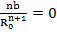 , (1.7)
, (1.7)
( 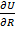 )R = Ro =
)R = Ro = 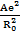
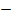
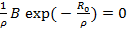 . (1.8)
. (1.8)
Это позволяет исключить константы b и В и перейти к уравнениям
U= 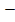
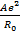 (1 -
(1 -  ) =
) = 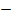
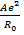
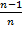 , (1.9)
, (1.9)
U = 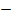
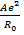 (1 -
(1 - 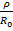 ). (1.10)
). (1.10)
Уравнение (1.9) называется уравнением Борна-Ланде, а (1.10) – Борна-Майера. Неизвестные параметры отталкивания n и 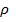 могут быть определены из данных по сжимаемости кристаллов, которая связана со второй производной
могут быть определены из данных по сжимаемости кристаллов, которая связана со второй производной 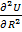 . Величина n изменяется от 6 для галогенидов Li до 13 для галогенидов Ag. Для не очень малых ионов щелочных металлов (NaCl, KCl) n = 9. Среднее значение
. Величина n изменяется от 6 для галогенидов Li до 13 для галогенидов Ag. Для не очень малых ионов щелочных металлов (NaCl, KCl) n = 9. Среднее значение 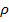 оказалось более постоянным и равным (0, 035
оказалось более постоянным и равным (0, 035 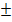 0,005) нм, при средних значениях межатомных расстояний R0 = 0,3 нм, энергия отталкивания составляет около 1/10 энергии решетки.
0,005) нм, при средних значениях межатомных расстояний R0 = 0,3 нм, энергия отталкивания составляет около 1/10 энергии решетки.
Энергетическая прочность решетки рассчитывается для 1моля и берется с обратным знаком:
U = 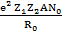
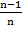 , (1.11)
, (1.11)
где Z1, Z2 – заряды ионов, N0 – число Авогадро. Формула (1.11) называется уравнением Борна.
Энергетическая прочность решетки – это та энергия, которая выделяется при образовании ионного кристалла из бесконечно удаленных ионов. Еще один способ определения энергетической прочности ионного кристалла – использование для расчета кругового процесса Борна – Габера.
Запишем цикл Борна – Габера для ионного кристалла МХ, где М – атом металла, Х – атом галогена. В квадратных скобках обозначены вещества в кристаллическом состоянии, в круглых скобках – вещества в газообразном состоянии. Рядом со стрелками, показывающими переход из одного состояния в другое, записаны энергетические изменения: энергия, выделяемая системой, считается со знаком (+), а затрачиваемая – со знаком ( - ):
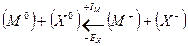
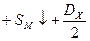
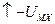
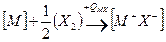 .
.
Для того, чтобы кристалл 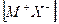 разложить на ионы
разложить на ионы 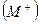 и
и 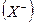 , требуется затратить энергию решетки UMX ; при превращении ионов в нейтральные атомы выделяется энергия ионизации катиона IM, а энергия EX, равная сродству галогена к электрону, затрачивается:
, требуется затратить энергию решетки UMX ; при превращении ионов в нейтральные атомы выделяется энергия ионизации катиона IM, а энергия EX, равная сродству галогена к электрону, затрачивается:
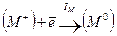 ,
,
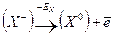 ;
;
при конденсации атомов металла освобождается энергия сублимации SM, а при образовании молекулы (Х2) из двух атомов галогена – выделяется энергия диссоциации молекулы на атомы DX. (Круговой процесс записывается для одного атома галогена в соответствии с химической формулой кристалла). Наконец, из кристалла металла [M] и газообразного галогена (Х2) снова возникает исходный кристалл 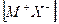 с освобождением теплоты образования кристалла из простых веществ QMX.
с освобождением теплоты образования кристалла из простых веществ QMX.
Так как в круговом процессе нет потерь энергии, составим баланс энергии:
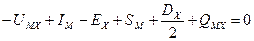 ,
,
откуда
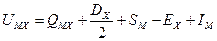 . (1.12)
. (1.12)
Все величины, стоящие в правой части равенства, могут быть определены экспериментально (из таблиц физико-хими- ческих величин). Поэтому такой метод определения энергии решетки называется «экспериментальным».
Энергия образования кристалла из простых веществ QMX с точностью до знака совпадает с энтальпией их образования из простых веществ 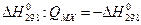 .
.
Для всех энергетических величин расчет ведется на 1 моль вещества, поэтому энергию сродства к электрону и энергию ионизации из электроновольт переводят в джоули на моль. 1 эВ = 1,6∙10–19 Дж. Умножив на число Авогадро NA = 6,02∙1023 моль–1, получим 96,48 кДж/моль.
Если заряд аниона отличен от единицы, то вместо ЕХ надо записать энергию присоединения п электронов 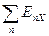 , при этом знак перед
, при этом знак перед 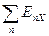 изменится на противоположный, так как энергия выделяется лишь при присоединении одного электрона к нейтральному атому, а при присоединении двух и более электронов энергия затрачивается. Например, для кислорода Е1 = 1,46 эВ (сродство к электрону); а при присоединении двух электронов
изменится на противоположный, так как энергия выделяется лишь при присоединении одного электрона к нейтральному атому, а при присоединении двух и более электронов энергия затрачивается. Например, для кислорода Е1 = 1,46 эВ (сродство к электрону); а при присоединении двух электронов 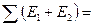 – 6,7 эВ.
– 6,7 эВ.
Если заряд катиона отличен от единицы, то вместо IM нужно взять сумму энергий ионизации 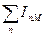 .
.
Круговой процесс записывается для всех ионов, которые входят в химическую формулу кристалла, например, для кристалла 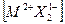 в круговом процессе будут участвовать один атом металла и два атома галогена.
в круговом процессе будут участвовать один атом металла и два атома галогена.
Если второй компонент не образует молекулы, а находится в твердом состоянии, например, сера, то вместо DX следует брать SX:
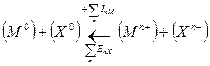
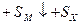
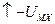
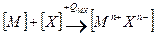 .
.
Формула для расчета прочности решетки примет вид
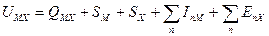 . (1.13)
. (1.13)
Ионные радиусы
По кратчайшему расстоянию в кристаллической решетке атомы или ионы касаются друг друга. Межионное (кратчайшее) расстояние R0 в ионном кристалле представляют как сумму радиусов катиона rk и аниона ra : R0 = rk + ra .
Существуют различные таблицы ионных радиусов, например, Гольдшмидта (эмпирические), Полинга (теоретические), Захариасена («эмпирико-теоретические») и др.
Значение ионного радиуса для одного и того же атома зависит от заряда иона: у катионов с увеличением заряда ионный радиус уменьшается, а у анионов – наоборот, возрастает.
Для большинства ионных решеток структура зависит от соотношения ионных радиусов. Кулоновское взаимодействие между ионами является ненаправленным и ненасыщенным.
Ненасыщенность проявляется в том, что каждый ион стремится приблизить к себе как можно больше противоположно заряженных ионов, т.е. образовать структуру с возможно более высоким координационным числом, т.е. создать плотную упаковку. Поэтому координационное число растет с увеличением размера катиона – рис.1.11.
Пределы изменения отношения радиуса катиона к радиусу аниона k = rк/rа , рассчитанные Магнусом и Гольдшмидтом для структур с различными координационными числами, приведены в таблице 1.3.
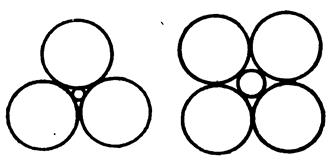
Рис. 1.11. Связь между конфигурацией атомов в координационной сфере и отношением ионных радиусов k = rк/rа
Таблица 1.3
Связь отношения ионных радиусов с координационными
числами ионных решеток
| Координационное число | Конфигурация ионов | Отношение радиусов k = rк/rа |
| Треугольник АХ3 | 0,153 ≤ k ≤ 0,225 | |
| Тетраэдр АХ4 | 0,225 ≤ k ≤ 0,414 | |
| Октаэдр АХ6 | 0,414 ≤ k ≤ 0,732 | |
| Куб АХ8 | 0,732 ≤ k ≤ 1,0 | |
| Плотная кубическая или гексагональная | 1,0 |
Ионные радиусы зависят от координационного числа.
Координационное число записывается в виде нижнего индекса у ионного радиуса, например, r4, r6, r8, r12.
Обычно в таблицах указываются радиусы для к.ч. = 6, что соответствует решетке типа NaCl.
Уменьшение к.ч. приводит к уменьшению ионных радиусов: при переходе от к.ч. = 12 к к.ч. = 6 – на 12 %, от к.ч. = 8 к к.ч. = 6 – на 4 %, от к.ч. = 4 к к.ч. = 6 увеличивается на 6 % .
Далеко не все структуры подчиняются правилу отношения ионных радиусов . Особенно это касается ионов с большими зарядами (Si+4, P+5, S+6, I+7), т.к. такие большие заряды энергетически невыгодны. Факт образования одними и теми же веществами модификаций с разными к.ч. свидетельствует о том, что проблема образования структур не может быть сведена к упаковке шаров данного диаметра.
