Основные определения и термины. Метод измерения электрической проводимости, иначе называемый кондуктометрией, относится к числу наиболее распространенных и точных способов изучения свойств

Метод измерения электрической проводимости, иначе называемый кондуктометрией, относится к числу наиболее распространенных и точных способов изучения свойств растворов электролитов.

Электрическая проводимость растворов электролитов – это их способность проводить электрический ток под действием внешнего электрического поля. Она обеспечивается за счет потоков миграции ионов, присутствующих в данном растворе. Электрическая проводимость L представляет собой величину, обратную сопротивлению проводника R:

L = 1/R . (8.1)

В Международной системе единиц (СИ) единицей электрической проводимости является сименс (См). Сименс равен электрической проводимости проводника сопротивлением в 1 Ом (1 См = 1 Ом ^–1).

Как и для обычных металлических проводников, сопротивление растворов рассчитывается по формуле

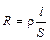, (8.2)

где r – удельное электрическое сопротивление; Ом·м (очевидно, что если l = 1м и S = 1м², то R = r); l – длина проводника (расстояние между электродами), м; S – площадь поперечного сечения проводника (для растворов – площадь электродов), м².

Подставив в уравнение (8.1) значение R из уравнения (8.2), получим

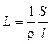, (8.3)

где 1/r – удельная электрическая проводимость, величина, обратная удельному сопротивлению. Обозначается она буквой c. С учетом этого обозначения уравнение (8.3) примет вид

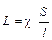. (8.4)

Если S = 1 м², l = 1 м, то L =χ.

Удельная электрическая проводимость раствора электролита – это электрическая проводимость объема раствора, заключенного между двумя параллельными инертными электродами, имеющими площадь по 1 м² и расположенными на расстоянии 1 м друг от друга. Она характеризует электрическую проводимость 1 м³ раствора, ее единицей является См/м. Удельная электрическая проводимость растворов электролитов зависит от природы электролита и растворителя, концентрации, температуры и других факторов.

Для однозначной характеристики проводящей способности растворов электролитов обычно пользуются значениями эквивалентной l и молярной l_m электрических проводимостей.

Эквивалентная электрическая проводимость l представляет собой проводимость раствора, помещенного между двумя параллельными электродами, расположенными на расстоянии 1 метра друг от друга, имеющими такую площадь, что объем раствора между ними содержит 1 моль эквивалента вещества, т.е. молярную массу эквивалента вещества (в случае молярной электрической проводимости l_m – 1 моль растворенного вещества).

Эквивалентная электрическая проводимость l выражается через удельную проводимость c:

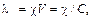(8.5)

где V – объем разбавленного раствора, м³, в котором содержится 1 моль эквивалента растворенного вещества, м³/моль; С – молярная концентрация эквивалентов электролита, моль/м³ (1 моль/л = = 10³ моль/м³).

В соответствии с представленными определениями и соотношением (8.5) единицей эквивалентной электрической проводимости в СИ является См×м²/моль.

В реальных системах эквивалентная электрическая проводимость зависит от концентрации и разбавления. С разбавлением раствора (уменьшением концентрации) эквивалентная электрическая проводимость l увеличивается, достигая при бесконечно большом разбавлении (при С ® 0) максимального и постоянного для каждого электролита значения. Это значение называется эквивалентной электрической проводимостью при бесконечном (предельном) разбавлении и обозначается l^¥или l⁰.

В бесконечно разбавленном растворе диссоциация электролита полная (степень диссоциации a = 1), ионы значительно удалены друг от друга. Взаимодействие между ионами отсутствует, они движутся независимо в электрическом поле. Поэтому эквивалентная электрическая проводимость при бесконечном разбавлении равна сумме предельных подвижностей ионов:

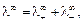(8.6)

где l^¥₊ и l^¥_– – предельные подвижности (или эквивалентные электрические проводимости) катиона и аниона:

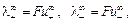(8.7)

где u^¥₊ и u^¥_– – абсолютные скорости движения ионов при бесконечном разбавлении, м²/(В×с); F – постоянная Фарадея, Кл/моль; F = 96485. Абсолютной скоростью движения иона называется его скорость при единичном градиенте потенциала в 1 В/м. Формула (8.6) выражает закон Кольрауша или закон независимого движения ионов, сущность которого заключается в том, что в растворе электролита катионы и анионы переносят электрический ток независимо друг от друга. Различие в подвижности ионов используется в кондуктометрическом методе анализа. Значения предельных эквивалентных электрических проводимостей (подвижностей) некоторых ионов в водном растворе представлены в прил. 2.

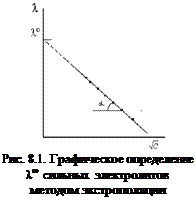Пользуясь известными значениями подвижностей ионов, можно вычислить согласно закону Кольрауша по формуле (8.6) эквивалентную электрическую проводимость электролита при бесконечном разбавлении. Непосредственное экспериментальное измерение предельной эквивалентной электрической проводимости при бесконечном разбавлении растворов электролитов λ^∞ невозможно.

Для определения λ^∞ растворов сильных электролитов наиболее пригоден метод экстраполяции, поскольку в области разбавленных растворов (при С меньше 10^–2 моль/л) λ находится в линейной зависимости от 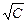(рис. 8.1) в соответствии с эмпирическим уравнением Кольрауша

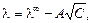(8.8)

где A – постоянная, зависящая от природы растворителя, температуры и валентного типа электролита; А = tg α.Эквивалентная электрическая проводимость сильных электролитов описывается уравнением (8.8) в большем интервале концентраций (до 0,002 моль/л) по сравнению с эквивалентной электрической проводимостью слабых электролитов. Линейная экстраполяция полученной прямой l = f( 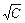) на нулевую концентрацию позволяет найти λ^∞ сильного электролита (как отрезок на ординате).

Метод экстраполяции для слабых электролитов не пригоден, так как для них зависимость l от 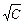не является линейной. Рассчитать λ^∞ слабого электролита можно по закону Кольрауша, если известна λ^∞ сильных электролитов, в состав которых входит тот или иной ион слабого электролита. Например, для уксусной кислоты – типичного слабого электролита:

.

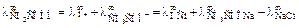В правой части последнего равенства находятся значения l^¥ сильных электролитов, которые могут быть определены методом экстраполяции или же вычислены (по данным таблиц в справочной литературе) как сумма предельных подвижностей катионов и анионов.

Данные об электрической проводимости растворов используются для определения степени и константы диссоциации слабых электролитов. Например, степень диссоциации слабого бинарного 1–1-валентного электролита определяется по уравнению Аррениуса

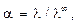(8.9)

где l – экспериментальное значение эквивалентной электрической проводимости при концентрации, к которой относится a; λ^∞ – эквивалентная электрическая проводимость при бесконечном разбавлении, рассчитываемая обычно по табличным данным как сумма предельных подвижностей ионов.

Константа диссоциации слабого бинарного 1–1-валентного электролита рассчитывается по результатам измерения электрической проводимости растворов в различных концентрациях по уравнению закона разбавления Оствальда

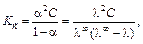(8.10)

где К_с – концентрационная (классическая или реальная) константа диссоциации.

Если табличные данные о подвижностях ионов отсутствуют, значения К_с и λ^∞ можно найти из экспериментальных данных по электрической проводимости растворов исследуемого электролита в нескольких концентрациях. Для этого придадим уравнению (8.10) вид

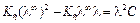(8.11)

и обе части поделим на 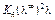. После небольших упрощений будем иметь

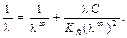(8.12)

Следует отметить, что для сильных электролитов

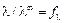, (8.13)

где ¦_l – коэффициент электрической проводимости.

Коэффициент f_l принимает значения меньше единицы (так как всегда l^¥>l). Значение ¦_l зависит от концентрации электролита и его валентного типа.

Измерение электропроводности растворов называют кондуктометрией. Кондуктометрию используют не только для определения степени и константы диссоциации электролитов, но и для определения концентрации электролитов в растворах, их растворимости.

Кондуктометрическое титрование – это метод определения концентрации по кондуктометрическим кривым титрования. Характер кривых титрования зависит от изменения количества ионов и их подвижности.

Рассмотрим два примера кондуктометрического титрования.

1. Титрование раствора сильной кислоты раствором сильного основания. Рассмотрим титрование соляной кислоты раствором гидроксида натрия

HCl + NaOH = H₂O + NaCl

или в ионной форме:

H⁺ + Cl^- + Na⁺ + OH^- = H₂O + Na⁺ + Cl^-.

В ходе титрования концентрация ионов С1^– остается постоянной, а ионы гидроксония связываются в малодиссоциирующее вещество – воду. Поэтому по мере нейтрализации проводимость раствора уменьшается, а в точке эквивалентности достигает минимума.

Добавление первой порции щелочи после точки эквивалентности приводит к резкому увеличению проводимости. Так как подвижность гидроксильных ионов меньше, чем ионов Н⁺, увеличение проводимости после точки эквивалентности происходит медленнее, чем ее падение до точки эквивалентности (рис. 8.2).

2. Титрование раствора слабой кислоты раствором сильного основания. Пример такого титрования – взаимодействие раствора уксусной кислоты и раствора гидроксида натрия

СН₃СООН + NaOH = CH₃COONa + H₂O

или в ионной форме:

CH₃COOH + Na⁺ + OH^- = CH₃COO^- + Na⁺ + H₂O.

При титровании слабой кислоты щелочью изменение электропроводности происходит вследствие повышения концентрации ионов, так как вместо слабо диссоциированной кислоты образуется ее полностью диссоциированная соль. Электропроводность повышается до эквивалентной точки постепенно, а затем резко – вследствие избытка ионов металла и ОН^-.

Добавление к раствору после достижения точки эквивалентности первой капли раствора NaOH приводит к значительному увеличению электрической проводимости электролита (рис. 8.3).

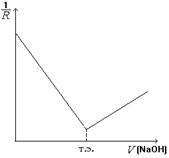V[NaOH] Рис. 8.2. Кривая кондуктометрического титрования сильной кислоты сильным основанием

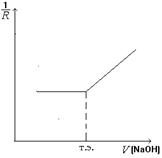V[NaOH] Рис. 8.3. Кривая кондуктометрического титрования слабой кислоты сильным основанием

ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ