Определение коэффициента линейного расширения проводника.

Лабораторная работа № 42

1. Цель работы: закрепление теоретических знаний по теме 5.2. “Реальные газы, жидкости и твердые тела”

приобретение практических навыков

изучение методики расчетов

2. Порядок подготовки к выполнению работы изучить теоретический материал и ответить на вопросы

3. Порядок выполнения лабораторной работы

4. Подведение итогов выполнения работы

предъявить результаты, подготовка и оформление отчета, заполнить таблички, произвести обработку результатов измерений

5. техника безопасности при выполнении лабораторной работы стандартная

Цель работы: Изучить тепловое движение микрочастиц в кристаллах и определить средний температурный коэффициент линейного расширения металла.

При нагревании кристаллических тел увеличивается амплитуда колебаний их атомов около положения равновесия в узлах кристаллической решётки. Однако этот факт не может служить причиной теплового расширения, т.к. в этом случае размеры цепочки атомов увеличивались бы только на удвоенную величину амплитуды таких колебаний, которая, в свою очередь, не превосходит расстояние между атомами, по порядку величины совпадающего с размерами самих атомов. Увеличение размеров тел при нагревании составляет заметную величину, гораздо большую размеров атомов.

Следовательно, причиной теплового расширения является изменение расстояний между атомами в кристаллической решётке. Для твёрдых тел экспериментально хорошо подтверждается формула

l=l₀(1+αΔt’),

где l₀- начальная длина стержня

l- длина стержня при нагревании на Δt градусов

α- коэффициент линейного расширения ( температурный) (ТКЛР).

Однако это соотношение не является универсальным даже при малых изменения температуры. Известны многочисленные отклонения от него. Все они объясняются тем, что кристаллическая решётка вещества может перестраиваться и при различных условиях оказывается устойчивым только определённый вид этой решётки.

Хорошо известно, что объём заданной массы воды минимален при температуре 4ºС. Это означает, что « стержень» из воды при 4ºС имеет α=0, при t^º > 4ºС α>0 и при t <4ºС α<0. Кроме воды такими же свойствами обладают и другие вещества.

Прибор позволяет определять ТКЛР стержней из различных материалов с высокой точностью, т.к. обеспечивает равномерный прогрев по длине стержня без использований водяной ванны или лучевого нагрева.

α= 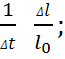Δl=l-l₀

Поэтому измерив начальную длину стержня l₀, удлинение стержня при нагреве Δl и определив изменение температуры стержня 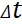º можно определить α.

Прибор также позволяет демонстрировать сокращение растянутой резиновой нити при нагревании. Этот эффект был обнаружен ещё 1805г. Гухом в экспериментах с полосками натурального каучука. Примерно через 50 лет Джоуль провёл ряд тщательных измерений и подтвердил вывод Гуха. Только полимеры в высокоэлластичном состоянии обладают таким свойством.

Температурным коэффициентом объемного расширения β называется относительное изменение объема V при нагревании тела на один кельвин

β = .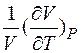

Для анизотропных веществ температурное расширение характеризуется температурным коэффициентом линейного расширения (ТКЛР) a, который определяется как

a = ,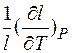

где l – размер тела в данном направлении.

Помимо коэффициентов a и β, которые называют истинными, для характеристики температурного расширения используют средние температурные коэффициенты расширения, определяемые, как средние значения истинных коэффициентов на конечном интервале температуры ∆Т:

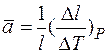; β = ,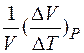

а также (для анизотропных веществ) средний по направлению ТКЛР a_ср = 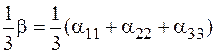. Единица измерения всех температурных коэффициентов расширения К^-1.

Существует приближенная феноменологическая связь между теплоемкостью С_V вещества при постоянном объеме и его изометрической сжимаемостью k_T, описываемая законом Грюнейзена:

β = g 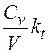, k_T = ,

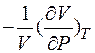где Р – давление; g - так называемая постоянная Грюнейзена, а также различные эмпирические соотношения, например

a ,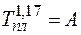

где Т_пл – температура плавления вещества; А = 7,24 · 10^-2 для веществ с металлическим характером связей, А = 11,5 · 10^-2 для щелочно – галлоидных соединений.

В общем случае a и β зависят от давления, температуры, химического состава, структуры тела и его фазового перехода, а также за счет сложения электронного, магнитного и решеточного вкладов в температурное расширение, которые в определенных температурных интервалах могут быть различными по знаку и сравнимыми по значению.

Описание установки:

Установка состоит из сопротивления МЛТ, внутри которого расположен медный стержень и термометр. Верхний конец стержня жестко фиксирован, а нижний упирается в штифт индикатора. При нагревании сопротивление от сети ~220В нагревается и стержень. При этом он расширяется, давит на штифт; в результате индикатор фиксирует удлинение.