Расчет количества теплоты для газопаровоздушной смеси
Например:найти количество теплоты, выделяющейся при взрыве 50 л смеси метана и этана в соотношении 1:4 при стандартных условиях.
Рассчитаем теплоту сгорания (− 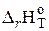 = Qн) метана и этана, опираясь на первое следствие из закона Гесса. Запишем термохимические уравнения реакции горения метана и этана в кислороде:
= Qн) метана и этана, опираясь на первое следствие из закона Гесса. Запишем термохимические уравнения реакции горения метана и этана в кислороде:
СН4(г)+ 2О2 = СО2(г) + 2Н2О(г)
2С2Н6(г) + 6 О2(г) + = 2СО2(г) + 6Н2О(г)
| вещество | 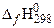 , кДж/моль , кДж/моль | вещество | 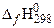 , кДж/моль , кДж/моль | вещество | 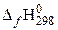 , кДж/моль , кДж/моль | вещество | 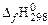 , кДж/моль , кДж/моль |
| СН4(г) | −74,85 | О2 | СО2(г) | −393,51 | Н2О(г) | 241,81 |
Согласно первому следствию из закона Гесса, теплота сгорания метана будет равна:
Qн= −[ 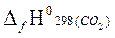 +2
+2 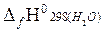 −
− 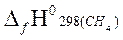 ] =
] =
= – [(−393,51)+2(−241,81)−(−74,85)] = 802,28 кДж/моль.
Значение низшей теплоты сгорания 1 м3 метана рассчитаем по формуле:
Qн, об = –(Qн×1000)/24,45,
где 24,45 л – объем одного моля газа при Т = 298 K.
Отсюда низшая теплота сгорания 1 м3 метана будет равна:
Qн, (СН4) = 802,28×1000 / 24, 45 = 32813,01кДж/м3.
| вещество | 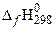 , кДж/моль , кДж/моль | вещество | 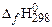 , кДж/моль , кДж/моль | вещество | 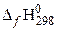 , кДж/моль , кДж/моль | вещество | 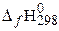 , кДж/моль , кДж/моль |
| 2С2Н6(г) | −84,67 | О2 | СО2(г) | −393,51 | Н2О(г) | 241,81 |
Низшая теплота сгорания 1 моля этана составит:
Qн= −[ 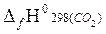 +2
+2 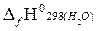 −
− 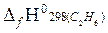 ] =
] =
= – [1(−393,51) + 3(−241,81)− (−84,67)] = 1034,27 кДж/моль.
Значение низшей теплоты сгорания 1м3 этана рассчитаем по формуле:
Qн, об = –(Qн×1000)/24,45,
где 24,45 л – объем одного моля газа при Т = 298 K.
Отсюда низшая теплота сгорания 1 м3 этана будет равна:
Qн, (С2Н6) = 1034,27×1000 / 24,45 = 42301,4кДж/м3.
Поскольку сгорает 50 л исходной газовой смеси в соотношении 1:4 (10 л метана и 40 л этана), то общая теплота сгорания 50 л смеси составит:
Qн = 32813,01 × 10-2 + 42301,4 ×· 4·10-3 = 497,34 кДж.
При взрыве 50 л смеси метана и этана в соотношении 1:4 при стандартных условиях выделится 497,34 кДж тепла.
Большинство химических реакций, в том числе реакций горения, протекают в изобарно-изотермических условиях, поэтому вопрос о термодинамической возможности их осуществления может решаться на основе анализа изменения энергии Гиббса реакции, определяемого по уравнению Гиббса-Гельмгольца:
DrG 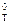 = DrН
= DrН 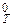 - Т. DrS
- Т. DrS 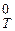 ,
,
где DrН 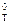 - изменение теплосодержания системы (тепловой эффект реакции для р = const) при температуре T; DrS
- изменение теплосодержания системы (тепловой эффект реакции для р = const) при температуре T; DrS 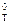 - изменение энтропии системы при той же температуре, причем:
- изменение энтропии системы при той же температуре, причем: 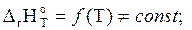
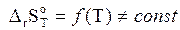
Анализ данного уравнения показывает, что знак и величина энергии Гиббса зависит от двух факторов энтальпийного (энергетического) DrН 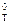 и энтропийного (вероятностного) DrS
и энтропийного (вероятностного) DrS 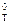 .
.
Рассмотрим варианты, возможные при осуществлении химических реакций, в частности реакций горения:
а) 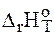 < 0;
< 0; 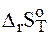 > 0 при этом
> 0 при этом 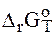 < 0 при всех значениях температуры, процесс термодинамически возможен при любойтемпературе;
< 0 при всех значениях температуры, процесс термодинамически возможен при любойтемпературе;
б) 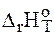 < 0;
< 0; 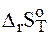 < 0 в этом случае
< 0 в этом случае 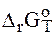 < 0 при
< 0 при 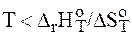 , т.е. реакция термодинамически возможна при сравнительно низкотемпературном режиме;
, т.е. реакция термодинамически возможна при сравнительно низкотемпературном режиме;
в) 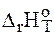 > 0;
> 0; 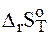 > 0, тогда
> 0, тогда 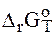 > 0 при
> 0 при 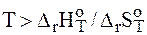 . следовательно, процесс термодинамически возможен при сравнительно высоких температурах;
. следовательно, процесс термодинамически возможен при сравнительно высоких температурах;
г) 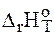 > 0;
> 0; 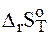 < 0 - оба фактора действуют в неблагоприятном направлении, реакция невозможна при любых температурах.
< 0 - оба фактора действуют в неблагоприятном направлении, реакция невозможна при любых температурах.
Стандартное изменение свободной энергии Гиббса реакции связано и с константой химического равновесия выражением
DrG 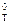 = - R·T·lnKr,
= - R·T·lnKr,
где DrG 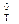 - стандартное изменение свободной энергии Гиббса при температуре Т, когда парциальное давление каждого из газообразных веществ перед началом реакции было равно 1 атм; R - газовая постоянная, равная 8,314 Дж/(моль·K); T - значение температуры, K; Kr - константа химического равновесия исследуемой реакции, выраженная через парциальные давления участвующих в реакции газообразных веществ.
- стандартное изменение свободной энергии Гиббса при температуре Т, когда парциальное давление каждого из газообразных веществ перед началом реакции было равно 1 атм; R - газовая постоянная, равная 8,314 Дж/(моль·K); T - значение температуры, K; Kr - константа химического равновесия исследуемой реакции, выраженная через парциальные давления участвующих в реакции газообразных веществ.
