Явление электромагнитной индукции 3 страница

, .

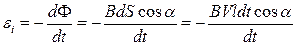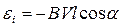2 При вращении рамки в магнитном поле. При изменении угла ориентации рамки α в магнитном поле изменение магнитного потока равно:

,

.

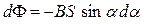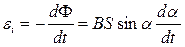При равномерном вращении 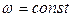, тогда 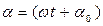. Следовательно,

.

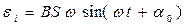3 При изменении модуля магнитной индукции:

.

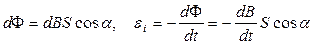Явление самоиндукции. Индуктивность.Если через контур течет ток, то создаваемое им магнитное поле пропорционально току: 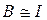, а собственный магнитный поток пропорционален магнитной индукции:

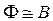. Следовательно, собственный магнитный поток пропорционален силе тока в контуре:

,

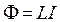где L – коэффициент пропорциональности между магнитным потоком и силой тока в контуре называется коэффициентом самоиндукцииилииндуктивностью.

В СИ: [L] = [Вб/А] = [Гн] (Генри).

ЭДС самоиндукции пропорциональна скорости изменения силы тока в контуре:

.

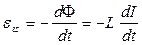Энергия магнитного поля:

.

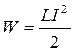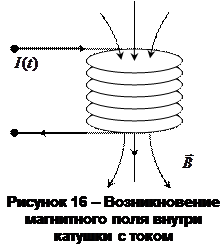
Объемная плотность энергии. Рассмотрим соленоид длиной l, площадью контура S, количеством витков N. Магнитное поле соленоида равно:

,

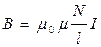где 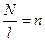– количество витков единицы длины соленоида. Магнитный поток через соленоид равен:

,

.

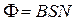Энергия магнитного поля соленоида: .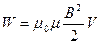

ПЕРЕМЕННЫЙ ТОК

Вынужденные электромагнитные колебания можно рассматривать как протекание переменного тока в цепи, содержащей резистор, катушку индуктивности и конденсатор. Переменный токможно считать квазистационарным,т.е. для него мгновенные значения силы тока во всех сечениях цепи практически одинаковы, так как их изменения происходят достаточно медленно, а электромагнитные возмущения распространяются по цепи со скоростью, равной скорости света. Для мгновенных значений квазистационарных токов выполняются закон Ома и вытекающие из него правила Кирхгофа.

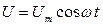Рассмотрим цепь, содержащую резистор, катушку индуктивности и конденсатор, при приложении к ней переменного напряжения: , где 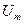– амплитуда напряжения.

Переменный ток, текущий через активное сопротивление.Сила переменного тока, текущего через резистор сопротивлением R (L→0, С→0) (рис. 17-а), при выполнении условия квазистационарности определяется законом Ома:

,

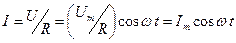где 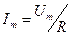– амплитуда силы тока.

На рис. 17-б дана векторная диаграмма амплитудных значений силы тока 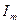и напряжения 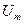на резисторе R, из которой видно,что сдвиг фаз между силой тока 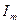и напряжением 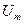равен нулю.

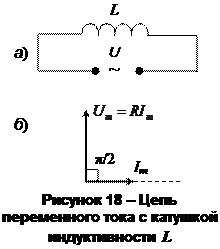
Переменный ток, текущий через катушку индуктивности.Если к цепи с катушкой индуктивности L (R→0, С→0) (рис. 18-а) приложено переменное напряжение 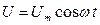, то в ней потечет переменный ток, в результате чего возникает ЭДС самоиндукции:

.

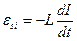Тогда закон Ома для рассматриваемого участка цепи имеет вид:

, .

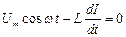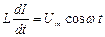Так как внешнее напряжение приложено к катушке индуктивности, то падение напряжения и сила тока катушке будут соответственно равны:

,

.

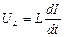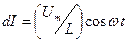После интегрирования с учетом того, что постоянная составляющая тока отсутствует, т.е. постоянная интегрирования равна нулю, получим:

,

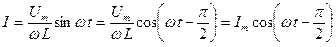где 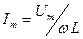– амплитудное значение силы тока.

Величина 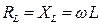называется реактивным индуктивным сопротивлением или индуктивным сопротивлением. Из этого выражения следует, что для постоянного тока ( 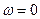) катушка индуктивности не имеет сопротивления.

Подставляя уравнение 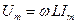в формулу 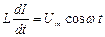, получим значение падения напряжения на катушке индуктивности:

.

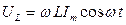Падение напряжения 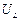опережает по фазе ток I, текущий через катушку, на π/2, что и показано на векторной диаграмме на рис. 18-б.

Переменный ток, текущий через конденсатор.Если к цепи с конденсатором электроемкости С (R→0, L→0) (рис. 19-а) приложено переменное напряжение 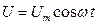, то конденсатор все время перезаряжается и в цепи потечет переменный ток. Так как все внешнее напряжение приложено к конденсатору, а сопротивлением подводящих проводов можно пренебречь, то:

.

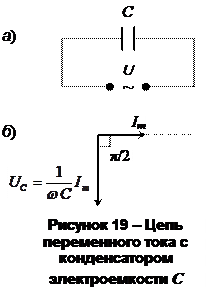
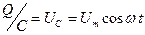По определению силы тока:

,

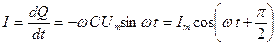где 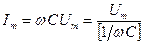– амплитудное значение силы тока в цепи с конденсатором электроемкости.

Величина 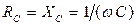называется реактивным емкостным сопротивлениемилиемкостным сопротивлением. Из этого выражения следует, что для постоянного тока ( 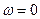) сопротивление конденсатора стремится к бесконечности ( 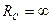), т.е. постоянный ток через конденсатор течь не может.

Падение напряжение на конденсаторе равно:

.

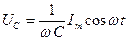Падение напряжения 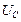отстает по фазе от тока I, текущего через конденсатор, на π/2 (рис. 19-б).

Цепь переменного тока.На концы цепи переменного тока, содержащей последовательно включенные резистор R, катушку индуктивности L и конденсатор С (рис. 20), подается напряжение 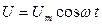. В цепи возникает переменный ток, который вызовет падения напряжения на всех элементах цепи: резисторе (U_R),катушке индуктивности (U_L),конденсаторе (U_C), что представлено на векторной диаграмме амплитуд падений напряжения (рис. 21). Амплитуда U_m приложенного напряжения равна векторной сумме амплитуд этих падений напряжений. Из диаграммы видно, что угол φ численно равен разности фаз между напряжением и силой тока и определяется формулой:

.

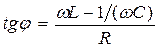По теореме Пифагора получаем: .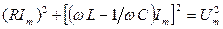

Откуда получаем значение амплитуды силы тока:

,

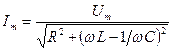совпадающей с амплитудой силы тока вынужденных электромагнитных колебаний.

Таким образом, если напряжение в цепи изменяется по закону ,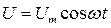

то в цепи течет ток .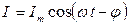

Величина 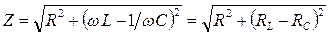называется полным сопротивлением цепи, а величина

–

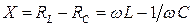реактивным сопротивлением.

Если в цепи переменного тока, содержащей последовательно включенные конденсатор, катушку индуктивности и резистор (рис. 20), индуктивное и емкостное сопротивления равны 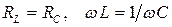,то угол сдвига фаз между током и напряжением обращается в нуль (φ = 0), т.е. изменения тока и напряжения происходят синфазно при резонансной частоте:

.

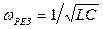Векторная диаграмма для резонанса напряжений приведена на рис. 22.

В случае резонанса напряжений падения напряжения на катушке индуктивности и конденсаторе равны: 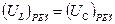, поэтому, подставив в эту формулу значения резонансной частоты и амплитуды напряжений на катушке индуктивности и конденсаторе, получим

,

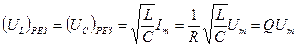где Q – добротность контура, определяемая выражением: .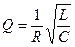

Мощность, выделяемая в цепи переменного тока.Мгновенное значение мощности переменного тока равно произведению мгновенных значений напряжения и силы тока: 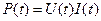, где 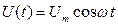, 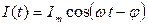. Подставив значения напряжения и силы тока в выражение для мощности и раскрыв 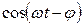, получим: .

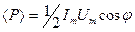Из векторной диаграммы (рис. 21) следует, что .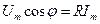

Поэтому при подстановке в выражение для среднего значения мощности получаем: .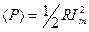

Такую же мощность развивает постоянный ток силой .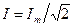

Величины 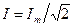и 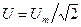называются соответственно действующими(или эффективными) значениями тока и напряжения.Все амперметры и вольтметры градуируются по действующим значениям тока и напряжения.

Учитывая действующие значения тока и напряжения, выражение средней мощности можно записать в виде

,

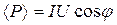где множитель 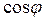называется коэффициентом мощности.

Коэффициент мощности показывает, что мощность, выделяемая в цепи переменного тока, в общем случае зависит не только от силы тока и напряжения, но и от сдвига фаз между ними. Если в цепи реактивное сопротивление отсутствует, то 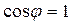и 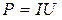. Если цепь содержит только реактивное сопротивление (R=0), то 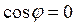и средняя мощность равна нулю, какими бы большими ни были ток и напряжение. Если 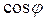имеет значения, существенно меньшие единицы, то для передачи заданной мощности при данном напряжении генератора нужно увеличивать силу тока I, что приведет, либо к выделению джоулевой теплоты, либо потребует увеличения сечения проводов, что повышает стоимость линий электропередачи. Поэтому на практике всегда стремятся увеличить 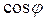, наименьшее допустимое значение которого для промышленных установок составляет примерно 0,85.

Трансформатор – прибор для трансформации переменного тока. Преобразование тока, при котором меняется его сила практически без изменения мощности, называется трансформацией.

Трансформатор представляет собой сердечник из трансформаторной стали, собранный из изолированных пластин. Первичная цепь состоит из генератора переменного тока, соединительных проводов и первичной катушки с числом витков n₁. Активное сопротивление катушки мало. Генератор поддерживает на катушке напряжение U₁. По второму закону Кирхгофа,

,

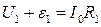где ε₁ – ЭДС самоиндукции первичной катушки, R₁ – ее активное сопротивление. ЭДС самоиндукции ε₁ складывается из ЭДС самоиндукции отдельных витков ε, так что

.

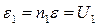Если бы в первичную цепь включили генератор постоянного тока, то через некоторое время ЭДС самоиндукции исчезла бы, индуктивного сопротивления не стало, и ток возрос до недопустимого значения 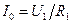– трансформатор бы сгорел. При работе генератора переменного тока ЭДС самоиндукции по правилу Ленца все время «мешает» генератору. Ток холостого хода I₀ мал, т.к. трансформатор при этом включен без нагрузки, а напряжение приблизительно равно 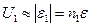. Опущенный знак минус относится к правилу Ленца.

Тот же переменный магнитный поток, который создает ЭДС самоиндукции ε в каждом витке первичной катушки, пронизывает витки вторичной катушки. Поэтому в каждом витке вторичной катушки возникает такая же по величине ЭДС индукции ε. Следовательно, на всей вторичной катушке наводится ЭДС индукции .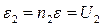

Отношение напряжений равно:

.

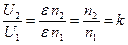Отношение чисел витков вторичной и первичной обмоток трансформатора называется коэффициентом трансформации k. Этот коэффициент равен отношению напряжений на вторичной и первичной катушках при разомкнутой вторичной цепи. Если k > 1, а U₂ >U₁ ,то трансформатор называют повышающим;если k <1, U₂ < U₁ – понижающим.

Пренебрегая потерями мощности, можно написать, что

,

.

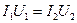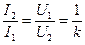Коэффициент полезного действия современных трансформаторов большой мощности доходит до 99%.

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

Задача 1.Определить силу взаимодействия двух точечных зарядов равных 3 мкКл и 6 мкКл, отстоящих друг от друга на расстояние 3 см в керосине. Диэлектрическая проницаемость керосина: ε = 2.

Решение

Согласно закону Кулона: .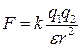

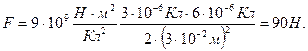
Задача 2.Две бесконечные параллельные пластины равномерно заряжены с поверхностной плотностью σ₁ =20 нКл/м² и σ₂ = – 40 нКл/м². Определить силу взаимодействия между пластинами, приходящуюся на площадь S, равную 0,5 м².

Решение

Напряженность поля создаваемого плоскостью в вакууме или воздухе: .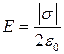

Заряд плоскости: .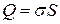

Сила действия одной плоскости на другую равна произведению напряженности поля, создаваемого одной плоскостью, на заряд другой плоскости:

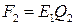, где .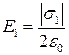

Тогда, сила взаимодействия между пластинами будет равна:

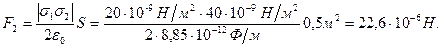
Задача 3.Тонкий стержень длиной l = 8 см несет равномерно распределенный заряд Q = 0,1 мкКл. Определить потенциал φ электрического поля в точке, лежащей на оси стержня на расстоянии а = 15 см от ближайшего его конца.

Решение

Напряженность 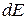поля создаваемого элементарным зарядом 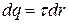на расстоянии 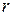определяется выражением: 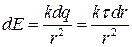, где 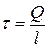– линейная плотность (рис. 24).

Таким образом, напряженность равна интегралу:

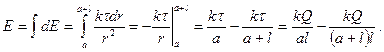
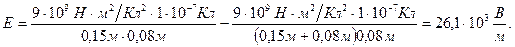
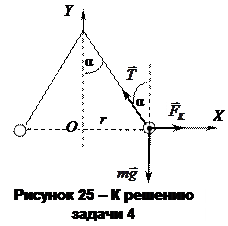Задача 4. Два одинаковых маленьких шарика подвешены на невесомых нитях длиной l = 12 см каждая в одной точке. Когда им сообщили одинаковые заряды Q = 4 нКл, шарики разошлись на угол α = 20⁰ (рис. 25). Найти силу натяжения каждой нити, если между шариками находится некоторая среда ε = 7,8.

Решение

Сделаем чертеж к задаче. На каждый из отклоненных шариков действуют силы: сила натяжения нити 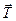, сила тяжести 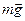и сила электростатического взаимодействия (отталкивания) шариков, то есть сила Кулона .

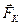Так как модули сил, действующие на шарики, одинаковы, то более подробно можно рассматривать только один из шариков, например правый (рис. 25).

Шарики находятся в равновесии под действием приложенных сил, поэтому согласно первому закону Ньютона запишем это условие равновесия:

.

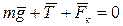Выберем прямоугольную систему координат XOY, связанную с одним из шариков, и перепишем это уравнение в проекциях на оси OX и OY:

ОY: , ,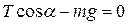

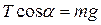ОХ: , .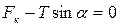

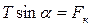По закону Кулона: 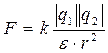, где r – расстояние между зарядами, ε – диэлектрическая проницаемость среды, 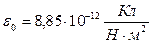– электрическая постоянная.

Из рис. 25 определим r: 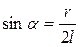, отсюда 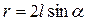. Полученное значение rподставляем в уравнение относительно оси OX:

,

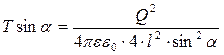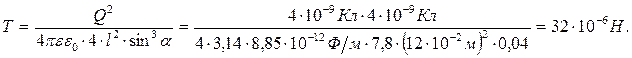
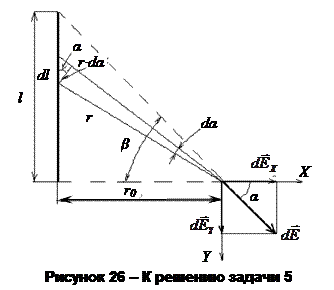Задача 5. Тонкий стержень длиной l = 10 см заряжен с линейной плотностью τ = 400 нКл/м. Найти напряженность Е электрического поля в точке, расположенной на перпендикуляре к стержню, проведенном через один из его концов, на расстоянии r = 8 см от этого конца.

Решение

Применим принцип суперпозиции для поля непрерывно распределенных зарядов:

.

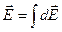Выделим на стержне бесконечно малый участок длиной dl (рис. 26). Находящийся на нем заряд 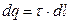можно считать точечным, и напряженность поля, созданного им, рассчитать как для точечного заряда:

.

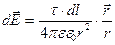Из рис. 26 видно, что: , .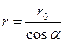

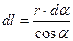Следует иметь в виду, что 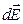– вектор, поэтому прежде чем интегрировать, выберем оси координат ОХ и ОУ найдем проекции вектора 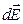на эти оси:

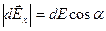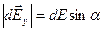, или , .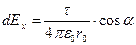

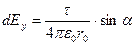Интегрируя эти выражения в пределах от 0 до β, получим:

,

,

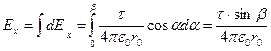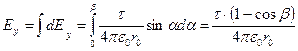где Е_х и Е_у – проекции результирующего вектора 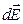на оси ОХ и ОУ.

Подставим числовые значения заданных величин в системе СИ и произведем вычисления:

,

.

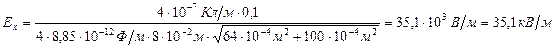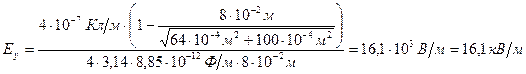Вектор напряженности определяется через проекции Е_х и Е_у:

,

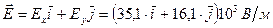где 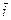и 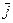- орты координатных осей ОХ и ОУ.

Модуль вектора напряженности найдем через его проекции на оси координат:

.

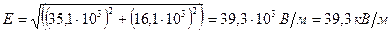Задача 6. Заряд равномерно распределен по бесконечной плоскости с поверхностной плотностью σ = 10 нКл/м². Определить разность потенциалов U двух точек поля, одна из которых находится на плоскости, а другая удалена от нее на расстояние r = 10 см.

Решение

Разность потенциалов 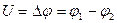двух точек в электростатическом поле определяется работой, совершаемой силами поля, при перемещении единичного положительного заряда из тки 1 в точку 2:

.

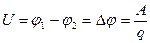Пользуясь определением напряженности электростатического поля, можем записать работу А в виде:

,

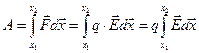отсюда:

.

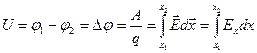Напряженность бесконечной плоскости с поверхностной плотностью σ:

,
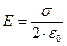