Идеальные и реальные электрохимические системы

Идеальные электрохимические системы — это такие идеализированные системы, в которых каждая из составных частей подчиняется законам идеального состояния и все процессы, которые могут в них протекать, также подчиняются законам этого состояния. Следовательно, если в идеальной системе есть газовая фаза, то это будет фаза идеального газа, уравнение состояния которого выражается формулой Клапейрона — Менделеева

PV = RT

a

(∂u/∂V)_T = 0

т. е. внутренняя энергия и моля газа не зависит от занимаемого им объема, что эквивалентно отсутствию всякого рода взаимодействий между молекулами газа. В этих формулах Р— внешнее давление, уравновешивающее давление газа, Па; V— мольный объем газа, м³/кмоль; R — универсальная газовая постоянная, являющаяся работой расширения (или сжатия) моля идеального газа при изменении температуры на один градус, Дж/(моль∙К), Т— температура, К.

Раствор в идеальной электрохимической системе также должен подчиняться законам идеальных растворов.

Поскольку концентрация С и объем V— величины обратно пропорциональные друг другу, то применительно к раствору уравнение состояния растворенного вещества будет иметь вид (здесь Р— осмотическое давление)

Р = CRT

a (∂u/∂V)_T = 0 превратится в

– C² (∂u/∂C)_T = 0

поскольку V = 1/С и dV = – (dC/C²).

Химический потенциал компонента в идеальном растворе, состоящем из m компонентов, выражается формулой

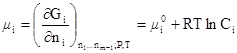
где G — энергия Гиббса; μ⁰_i – стандартный химический потенциал. Электрохимический потенциал выражается формулой:

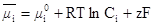
Индивидуальную фазу твердого или расплавленного электролита, а также проводника первого рода равным образом следует считать подчиняющимся законам идеального состояния.

Если в идеальной системе рассматриваются какие-нибудь гомогенные равновесия, например типа

aA + bB = cC + dD

то они будут определяться уравнением закона действующих масс, выраженного через равновесные концентрации

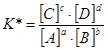
причем константа равновесия К будет зависеть только от температуры.

Направленные процессы в идеальных электрохимических системах, например, одномерная диффузия, будут подчиняться первому и второму законам Фика, выраженным через концентрации

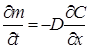
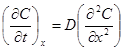
Первый закон Фика, описывающий процесс стационарной диф- фузии, связывает прямой пропорциональностью количество вещества т, диффундирующего в единицу времени (скорость диффузии) через единицу поверхности, и градиент концентрации. Константа пропорциональности (коэффициент диффузии D)из первого закона Фика выражается в квадратных метрах па секунду и не зависит от концентрации диффундирующего вещества.

Второй закон Фика дает изменение концентрации во времени t на расстоянии х от границы как функцию производной градиента концентрации и применим для случая нестационарной диффузии.

Уравнения скорости электрохимических реакций будут выражаться через концентрации, константу скорости и энергию активации, причем последняя является функцией разности потенциалов на границе раздела фаз (см. 8.2). Константа же скорости является функцией только температуры, но не концентраций.

Отклонение электрохимических систем от идеального состояния проявляется обычно в виде зависимости от концентраций тех величин в соответствующих уравнениях, которые по физическому смыслу от концентрации не должны зависеть (например, внутренняя энергия, константы равновесия, диффузии и скорости реакции).

В реальных электрохимических системах нужно учитывать разнообразные взаимодействия между компонентами и, следовательно, возможные отклонения в поведении систем по сравнению с идеальными.

Поясним это на примере газового состояния вещества. Уравнение состояния идеального газа PV = RT оказывается более или менее справедливым, когда газ находится в состоянии крайнего разрежения. Тогда расстояния между отдельными молекулами настолько велики, что силами взаимодействия между молекулами можно пренебречь. Кроме того, расстояния между молекулами оказываются много больше собственных размеров молекул и их можно считать геометрическими точками. Однако при переходе к большим давлениям уже нужно учитывать силы притяжения и отталкивания между молекулами и собственным объемом молекул уже пренебречь нельзя. Для учета влияния этих факторов приходится создавать определенные модели, которые неизбежно будут только в какой-то степени приближением к объективной реальности. Так, Ван-дер-Ваальс для объяснения поведения реальных газов предположил, что, во-первых, силы притяжения между молекулами, увеличивающие внешнее давление, обратно пропорциональны квадрату мольного объема а/V², во-вторых, что силами отталкивания при не очень больших давлениях можно пренебречь и, в-третьих, что мольный объем не может быть меньше собственного объема молекул b.

Исходя из этих предположений, уравнение состояния газа должно быть переписано так

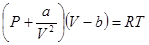
где а и Ь — константы, индивидуальные для каждого газа.

Если в левой части уравнения Ван-дер-Ваальса перемножить члены, стоящие в скобках, и вынести PVза скобки, то получим:

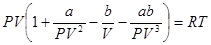
Обозначим теперь выражение в скобках через f. Тогда

fPV= øV = RT

Мы пришли вновь к уравнению типа уравнения идеального газа, но в нем появилась вместо давления новая переменная ø, связанная с давлением коэффициентом f, сложным образом зависящим от давления и объема. Знание коэффициента f дает возможность применять это уравнение для описания поведения реальных газов в рамках модели Ван-дер-Ваальса. Для более точных моделей реального газа f будет еще более сложной величиной.

Определение поправочного коэффициента f возможно двумя путями. Один путь — рациональный — это, как указано выше, путь теоретического расчета на основе определенных предположений о природе взаимодействий между частицами, приводящих к отступлению системы от идеального состояния.

Другой путь предложен в 1901 г. Г. Льюисом. Согласно идее Льюиса, давление и концентрация в уравнениях состояния и химического потенциала для идеального случая заменяются новыми величинами, подстановка которых в эти уравнения делает их пригодными для реального состояния. Эти величины связаны с давлением и концентрацией не прямо пропорциональной зависимостью. Величина, заменяющая в уравнениях давление, названа фугативностью ø, а концентрацию — активностью а.

Активность и фугативность представляют собой, следова-тельно, ту эффективную концентрацию и соответственно давление, которыми должны были бы обладать реальные раствор или газ, чтобы вести себя как находящиеся в идеальном состоянии.

В. К. Семенченко отмечает, что метод Льюиса до некоторой степени аналогичен методу теории относительности Эйнштейна. Как теория относительности сохраняет (в своей специальной части) основные законы динамики, вводя понятие о переменной массе, зависящей от условий, в которых находится система, так и теория активности пытается сохранить формулировки термодинамических соотношений при помощи обычного вида потенциалов (химических), вводя понятие об эффективной концентрации (активности), зависящей от окружающих условий.

Таким образом, согласно идее Льюиса, уравнение состояния, химического и электрохимического потенциалов и закона действующих масс записываются в виде:

øV = RT: Р = aRT

μ_i = μ⁰_i + RT ln a_i

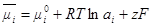
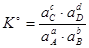
Сравнивая эти уравнения с уравнениями для идеального состояния, видим, что

ø/P = f и a/C = γ

где f и γ — соответственно коэффициенты фугативности и активности.

Метод активности, строго говоря, термодинамический метод. Поэтому с помощью активностей или фугативностей можно рассчитывать равновесие в реальных случаях. Что же касается процессов, направленно протекающих во времени, то для них применение метода Льюиса требует обоснования.

В отношении процесса диффузии Гиббс предположил, что поскольку этот процесс достаточна -медленный, его можно рассматривать как протекающий через ряд квазиравновесных состояний. Поэтому движущей силой процесса диффузии можно считать градиент химического потенциала. Тогда для потока диффузии записываем:

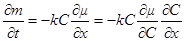
Но для реального вещества из уравнения μ = μ⁰ + RT ln a

имеем:

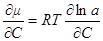
Подставив это выражение в уравнение для потока диффузии и помня, что ∂C/C = ∂ln C, получим:

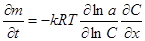
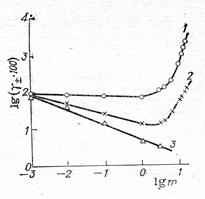
Рис. 2.7. Зависимость логарифма среднего ионного коэффициента активности γ_± от логарифма концентрации С электролита при 25 °С для водных растворов:

1— КОН; 2 — H₂SO₄; 3 — сульфаты тяжелых цветных металлов.

Заменив активность концентрацией и коэффициентом активности, данное уравнение переписываем так:

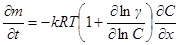
Обозначив 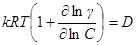мы вновь приходим к уравнению первого закона Фика с той лишь разницей, что реальный коэффициент диффузии, вообще говоря, оказывается зависящим от концентрации.

Из полученной формулы следует, что первый закон Фика в целом ряде случаев может оказаться справедливым в концентрационной форме даже для условий, далеких от идеальных. Для этого нужно лишь, чтобы логарифм коэффициента активности линейно изменялся с логарифмом концентрации. Тогда производная логарифма коэффициента активности по логарифму концентрации является постоянной величиной и коэффициент диффузии оказывается независимым от концентрации, хотя и не равным коэффициенту диффузии идеальной системы. Впрочем, производная часто имеет небольшое численное значение, т. е. выражение в скобках уравнения потока диффузии не сильно отличается от единицы. Для иллюстрации сказанного на рис. 2.7 приведены зависимости логарифма коэффициента активности от логарифма концентрации для водных растворов КОН, H₂SO₄ и сульфатов тяжелых цветных металлов. Из рисунка легко определяются те интервалы концентраций, в которых можно пользоваться первым законом Фика, выраженным через концентрации.

Возможность применения понятия активности в кинетике химических реакций обосновывается теорией активированного комплекса Эйринга. Согласно этой теории, скорость реакции определяется скоростью распада активированного комплекса, а исходные вещества и продукты реакции находятся в равновесии с активированным комплексом, причем продукты реакции не влияют на равновесие, предшествующее замедленной стадии. Следовательно, для реакции

A = B

можем записать

A = A^≠; A^≠ = B

где А^≠ — активированный комплекс.

Для скорости распада активированного комплекса справедливо уравнение Аррениуса

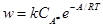
(здесь A – энергия активации; 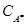– концентрация активированного комплекса), а для стадии образования активированного комплекса – формула закона действующих масс:

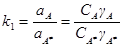
Подставив значение 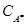из этого выражения в уравнение скорости, получим:

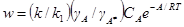
Поскольку весьма вероятно, что коэффициент активности активированного комплекса не зависит от концентрации реагирующих веществ, то 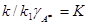и

w = Kγ_AC_Ae^–A/RT = Ka_Ae^–A/RT

Таким образом, получается кинетическое уравнение для скорости химической реакции, в которое входит не концентрация, а активность вещества, вступающего в реакцию.

МЕТОД АКТИВНОСТИ

Отклонение электрохимических систем от идеального состояния происходит главным образом из-за неподчинения законам идеального состояния электролитов. Причиной этих отклонений является в первую очередь наличие сил межионного и ион-дипольного взаимодействия. Очевидно, что в растворах, содержащих нейтральные молекулы, когда отсутствуют кулоновские силы взаимодействия, отклонения от идеальности будут наблюдаться при более высоких концентрациях вещества, чем в электролитах. В электролитах силы межионного взаимодействия возрастают в результате появления дальнодействующих электростатических взаимодействий, что обусловливает их существенное отличие от молекулярных растворов. Поэтому значения коэффициентов активности для растворов нейтральных молекул с увеличением концентрации изменяются значительно меньше, чем в растворах электролитов. Дальние взаимодействия в разбавленных растворах в основном сводятся к появлению сил притяжения между противоположно заряженными ионами и сил отталкивания между одноименно заряженными ионами. При возрастании концентрации силы притяжения приводят к образованию ионных пар или ассоциатов, в результате чего уменьшается число ионов в единице объема. В высококонцентрированных растворах, когда отношение числа ионов в единице объема к числу молекул растворителя превышает границу полной сольватации (К. П. Мищенко и А. М. Сухотин), начинается конкуренция между ионами разных сортов за обладание молекулами растворителя, ибо за границей полной сольватации не хватает молекул растворителя для нормального заполнения координационных сфер ионов. Это приводит к еще большему отклонению состояния электролита от идеального. Наконец, при очень больших концентрациях следует учитывать и силы отталкивания.

Такой сложный комплекс взаимодействий, а также те взаимодействия, которые не могут быть полностью учтены с электростатических позиций (например, комплексообразование), сильно отражаются на значении коэффициента активности.