Простая гидродинамическая теория

Полученное выше уравнение для скорости движения иона

w⁰ = ez/L

дает возможность теоретически решить проблему электрической проводимости, если будет установлена функциональная зависимость коэффициента пропорциональности L уравнения L' = Lw от параметров, определяющих скорость движения иона. К таким параметрам в первую очередь относятся концентрация, природа электролита и растворителя, температура.

Для определения L можно воспользоваться уравнением Стокса, согласно которому коэффициент сопротивления движению шара в вязкой непрерывной среде определяется выражением

L = 6πηr

где η — динамическая вязкость среды; r— радиус шара (часто, называемый стоксовым радиусом).

Если считать это уравнение применимым к нашему случаю, то нужно допустить, что ионы можно представить себе в виде шаров, двигающихся в непрерывной вязкой среде, т. е. что можно пренебречь размерами молекул растворителя по сравнению с размерами ионов, что вязкость структурированных слоев растворителя вокруг ионов, которые собственно и оказывают сопротивление движению последних, такая же, как и вязкость (коэффициент внутреннего трения) чистого растворителя, и что, наконец, силами взаимодействия между ионами можно пренебречь. Кроме того, уравнение будет оправдываться только при независимости rот указанных выше факторов.

Подставим это выражение в формулу скорости движения иона. Поскольку требуемое отсутствие сил взаимодействия между ионами наиболее вероятно в бесконечно разбавленных растворах, мы все дальнейшие формулы запишем именно для этого случая. Поэтому w⁰_∞ = ez/6πηrи для удельной электрической проводимости:

Выражение для эквивалентной электрической проводимости, следовательно, можно записать в виде

откуда подвижность катиона и аниона равны:

и

Из этих уравнений видно, что радиусы ионов могут быть определены из значений их подвижности. Рассчитанные таким образом стоксовы радиусы r_Sионов в водных растворах при 25 °С сопоставлены с кристаллографическими радиусами;

r_S, нм r, нм r_S, нм r, нм

Li⁺ 0,237 0,060 N(CH₃)₄⁺ 0,204 0,347

Na⁺ 0,183 0,097 N(C₂H₅)₄⁺ 0,281 0,400

Be²⁺ 0,408 – N(C₃H₇)₄⁺ 0,392 0,452

Mg²⁺ 0,346 0,065 N(C₄H₉)₄⁺ 0,471 0,494

Ca²⁺ 0,309 0,099 N(C₅H₁₁)₄⁺ 0,525 0,529

Sr²⁺ 0,309 0,113

Ba²⁺ 0,288 0,135

Zn²⁺ 0,346 0,074

La³⁺ 0,395 0,115

Стоксовы радиусы ионов для всех приведенных в таблице простых ионов оказались больше кристаллографических. Кроме того, в ряду одновалентных ионов металлов первой группы периодической системы Д. И. Менделеева оказалось, что при переходе от лития к цезию изменение кристаллографического радиуса обратно изменению стоксового радиуса. Это однозначно свидетельствует о том, что ионы в водной среде двигаются вместе со своими гидратными оболочками. А гидратные оболочки и числа гидратации при одинаковой валентности ионов, естественно, будут тем больше, чем меньше радиус иона. Что касается комплексных ионов, то чем больше их радиусы, тем меньше разница между r и r_S.Следовательно, большие комплексные ионы практически не гидратированы. Вообще говоря, числа гидратации, определенные разными методами, сильно отличаются друг от друга. Например, число гидратации иона лития колеблется от 160 до 2; иона натрия — от 66 до 1. Такое расхождение нельзя объяснить неточностью методов, так как и в пределах одного и того же метода. Цифры, полученные разными исследователями, сильно расходятся (для иона лития — от 160 до 5, для иона калия — от 29 до 7, для иона хлора — от 27 до 5 и т. д.). Ниже приведены средние числа гидратации некоторых ионов, предлагаемые Робинсоном и Стоксом, с помощью которых они добились наилучшего совпадения рассчитанных по их формуле коэффициентов активности с экспериментально установленными величинами (см. 3.3):

Электролит Число Электролит Число Электролит Число гидратации гидратации гидратации

LiC1 10,5 NaCl 7,9 КС1 3,4

LiBr 9,0 NaBr 6,4 КВг 1,9

LiNO₃ 4,4 NaNO₃ 1,8 KNO₃ –2,7

LiClO₃ 6,3 NaC1O₃ 3,7 KC1O₃ –0,8

LiBrO₃ 9,2 NaBrO₃ 6,6 KBrO₃ 2,1

LiIO₃ 7,7 NaIO₃ 5,1 КIО₃ 0,6

Эквивалентная электрическая проводимость раствора может быть определена из подвижностей ионов и чисел переноса;

l_+∞= λ_э∞t_+∞; l_–∞= λ_э∞t_–∞

причем сумма подвижностей, полученных из измерений электрической проводимости различных электролитов, точно равна электрической проводимости при бесконечном разведении электролита. Например, для бинарного электролита

λ_э∞ = l_+∞ + l_–∞

Это соотношение называется законом независимого движения ионов Кольрауша и применимо к растворам при бесконечном разведении, так как при этих условиях становятся несущественными силы взаимодействия между ионами, а последние можно рассматривать как шары, двигающиеся независимо друг от друга.

Из выражения для эквивалентной электрической проводимости непосредственно получается, что

λ_э∞η_∞ = const

(правило Вальдена—Писаржевского). Произведение эквивалентной электрической проводимости на коэффициент внутреннего трения не зависит от концентрации растворенного вещества, природы растворителя, температуры и любого другого фактора, если не зависят от этих величин стоксовы радиусы ионов.

С помощью правила Вальдена — Писаржевского легко проверяется справедливость исходных предпосылок простой гидродинамической теории. Для больших ионов органических соединений, обладающих к тому же единичной валентностью, правило Вальдена — Писаржевского вполне применимо, поскольку эти ионы, как отмечено выше, практически не сольватированы и силы притяжения между ними невелики.

Влияние природы растворителя исследовано на примере пипе-ридинпикрата, растворенного в разных растворителях (при 25°С):

λ_э∞η_∞∙10⁸

Растворитель

Вода 0,62

Метиловый спирт 0,57

Этиловый спирт 0,54

Ацетон 0,53

Бензонитрил 0,50

Нитрометан 0,58

Из приведенных данных следует, что в довольно широком интервале изменений вязкости и эквивалентной электрической проводимости правило Вальдена — Писаржевского действительно хорошо соблюдается. Независимость произведения λ_э∞η_∞ от температуры можно показать на примере водного раствора пикрата тетраэтиламмония:

t, ºС 0 18 100

λ_э∞η_∞∙10⁸, 0,556 0,563 0,560

Наконец, постоянство значений λ_э∞η_∞для разных концентраций растворенного вещества проиллюстрируем на примере метафосфата натрия (NaPO₃, или Na₂O∙P₂O₅), растворенного в расплавленном борном ангидриде (В₂О₃), который сам не проводит электрический ток и является своеобразным растворителем (900 °С):

, % (масс.) 100 50 5 0,5

λ_э∞η_∞∙10⁸, 74,3 73,8 73,3 73,7

Расчет радиусов иона гидроксония и гидроксид-иона в водной среде показал, что их стоксовы радиусы меньше кристаллографических. Следовательно, перенос тока в водных растворах кислот и оснований происходит не так, как в других случаях *.

* Механизм переноса тока в кислотах и основаниях рассмотрен дальше (см. 5.1.3.4).

Рис. 5.10. Зависимость эквивалентной электрической проводимости иодида лития от концентрации в органическом растворителе с различной диэлектрической проницаемостью.

Не менее существенно, чем вязкость, на электрическую проводимость растворов влияет и другое свойство растворителя — диэлектрическая проницаемость, которая частично определяет его ионизирующую способность и изменяет силы электростатического взаимодействия между ионами. Следовательно, в конечном итоге диэлектрическая проницаемость влияет на число ионов в единице

объема и на число сольватации. Для того, чтобы можно было разделить влияние вязкости и диэлектрической проницаемости, А. Н. Саханов ввел понятие корригированной электрической проводимости λ_к, т. е. электрической проводимости, учитывающей изменение вязкости раствора

λ_к = λη/η₀

где ηи η₀ — соответственно вязкость раствора при данной концентрации и чистого растворителя. Отношение η/η₀ всегда больше единицы, поэтому корригированная (исправленная) электрическая проводимость всегда выше измеренной.

На рис. 5.10 по данным А. М. Сухотина представлено изменение эквивалентной электрической проводимости иодида лития с концентрацией в смешанном растворителе — бутанол + гексан. Изменяя соотношение бутанола и гексана, можно в широком интервале изменять диэлектрическую проницаемость ε смешанного растворителя.

При низких концентрациях зависимость λ — С в логарифмических координатах линейна, причем угол наклона прямой равен '/₂. Однако с уменьшением диэлектрической проницаемости растворителя при больших концентрациях соли наблюдается аномалия. Появляются участки роста эквивалентной электрической проводимости с концентрацией, причем минимум на кривой оказывается при тем меньшей концентрации, чем меньше диэлектрическая проницаемость. Дальнейшее увеличение концентрации электролита при низких ε приводит к максимуму на кривой и новому ниспадающему участку.

Уменьшение эквивалентной электрической проводимости с ростом концентрации, по Бьерруму, происходит из-за ассоциации ионов с образованием ионных пар. Например, для того же иодида лития ионные пары образуются по схеме:

Li⁺ + I^– = [Li⁺I^–]

В результате часть ионов ассоциирует в нейтральные частицы, не проводящие ток. Следовательно, общее число ионов с ростом концентрации уменьшается и значение эквивалентной электрической проводимости падает.

Аномальный рост эквивалентной электрической проводимости в области больших концентраций Бьеррум объясняет взаимодействием нейтральных ионных пар с образованием ионных тройников

2[Li⁺I^–] = Li⁺ + [Li⁺2I^–]^– или 2 [LiI^–] = I^– + [2Li⁺I^–]⁺

приводящим к увеличению числа ионов и росту λ_э.

Наконец, последняя ниспадающая ветвь кривой λ_э — С с этих позиций объясняется образованием еще более сложных нейтральных частиц — квадруполей:

Li⁺ + [Li⁺2I^–] = [2Li⁺2I^–] или I^– + [2Li⁺I^–]⁺ = [2Li⁺2I^–]

Однако, по А. М. Сухотину, реально образуются лишь ионные пары. Что касается аномального хода кривой эквивалентной электрической проводимости, то он может быть объяснен без предположения об ионных тройниках и квадруполях, но с учетом изменения коэффициента активности.

Рассмотрим этот вопрос подробнее. Допустим, что иодид лития полностью диссоциирован на простые ионы Li⁺ и I^–, которые могут ассоциировать в ионные пары. Следовательно, наблюдается равновесие, определяемое реакцией Li⁺ + I^– = [Li⁺I^–]. Степень диссоциации ассоциатов обозначим через α. Тогда при концентрации иодида лития, равной С, концентрация свободных ионов лития и иода будет αС, а концентрация ассоциатов (1 – α)С. Константа равновесия реакции ассоциации может быть записана в виде:

или

Подставив вместо α отношение λ_э/λ_э∞, получим уравнение, совершенно аналогичное по виду уравнению закона разведения Оствальда;

Когда равновесие сдвинуто вправо, т. е. α << 1, то уравнение Оствальда можно записать в виде

или в. логарифмической форме:

Из этого уравнения следует, что в логарифмических координатах зависимость λ_э— С изображается прямой линией с угловым коэффициентом

что находится в полном соответствии с данными, приведенными на рис. 5.10.

Если же в уравнении Оствальда нельзя пренебречь значением α по сравнению с единицей, то для графической проверки переписываем это уравнение так:

Поделив на λ_э и решив его относительно 1/λ_Э, получаем:

Следовательно, для этого случая экспериментальные данные по зависимости λ_э от С должны расположиться вдоль прямой линии в координатах 1/λ_э — λ_эС. Так как эквивалентная электрическая проводимость при бесконечном разведении легко определима из ионных подвижностей, то из угла наклона прямолинейного участка вычисляется константа ассоциации электролита.

При увеличении температуры электрическая проводимость растворов возрастает и достаточно точно может быть представлена уравнением

λ_эt = λ_{э 25} [1 + α(t – 25) + β(t – 25)²]

где λ_эt и λ_{э 25} — эквивалентные электрические проводимости при искомой температуре и 25 °С соответственно; αи β — коэффициенты, постоянные в определенном интервале температур (зависят как от природы растворенного вещества, так и от природы растворителя).

В узком интервале температур квадратичным членом можно пренебречь из-за его малости. По аналогичному уравнению происходит изменение и подвижностей ионов при бесконечном разведении (l_∞), причем коэффициент α для большинства ионов близок к 0,02 (кроме НзО⁺, для которого α = 1,42∙10^–2 , и ОН^– – α = 1,6∙10^–2).

Влияние температуры на эквивалентную электрическую проводимость часто может быть представлено экспоненциальной зависимостью

где k — константа, не зависящая от температуры; А — энергия активации электрической проводимости. Дифференцируем по температуре:

Если же продифференцировать по температуре уравнение, выражающее температурную зависимость λ_э в виде многочлена, отбросив в нем все члены в степени выше первой, то получим:

Из сравнения последних двух выражений следует:

А = αRT²

По этому уравнению численное значение энергии активации А при 25 °С и α = 0,02 равно ~ 15 кДж/моль. Аналогичные значения энергии активации наблюдаются и для зависимости κ— Т, так как λ_эв уравнениях можно заменить на пропорциональную ей величину κ, при этом значение коэффициента α не изменится. В связи с тем, что αдля иона гидроксония и гидроксид-иона меньше, энергия активации электрической проводимости для них ниже.

Значение энергии активации электрической проводимости может быть найдено и непосредственно из экспоненциальной зависимости, электрической проводимости от температуры аналогично тому, как это изложено в разд. 5.1.2.2.

Значения энергии активации, определенные таким образом, оказываются в пределах 12 — 17 кДж/моль, что совпадает со значениями энергии активации вязкого течения жидкости. Такое совпадение энергий активации двух процессов говорит в пользу того, что электрическая .проводимость определяется движением шаровых ионов в вязкой среде.

5.1.3.2. ТЕОРИЯ ДЕБАЯ – ХЮККЕЛЯ – ОНЗАГЕРА

В этой теории модель строения раствора такая же, как и при расчете коэффициентов активности. Ион под влиянием 'наложенного электрического поля начинает двигаться. На скорость его движения тормозящее действие оказывает ионная атмосфера, поскольку она имеет электрический заряд, противоположный по знаку заряду центрального нона, и поэтому под влиянием электрического поля двигается в направлении, обратном направлению иона (рис. 5.11). Вторая причина торможения связана с тем, что образование и разрушение ионной атмосферы происходит не мгновенно. Хотя на образование ионной атмосферы требуется очень небольшое время — порядка 10^–10/С с (С — концентрация), все же при движении иона ионная атмосфера не успевает в каждый данный момент восстанавливать свою сферическую симметрию. Она все время остается асимметричной, причем большая часть ее заряда оказывается сконцентрированной позади двигающегося центрального иона. Это приводит к дополнительному торможению движения иона (рис. 5.12).

Первый эффект торможения называется электрофоретическим, а второй — релаксационным. Общий эффект является суммой

Рис. 5.11. Схема электрофорeтического эффекта.

Рис. 5.12. Схема релаксационного эффекта.

электрофоретического и релаксационного эффектов торможения. При расчете электрофоретического эффекта считают, что релаксационный эффект отсутствует, в то время как при расчете релаксационного эффекта допускают отсутствие электрофоретического эффекта. Электрофоретический эффект в рассматриваемой теории рассчитывают следующим образом. Скорость движения i-гo иона при градиенте потенциала, равном единице, и в отсутствие ионной атмосферы приравнивается абсолютной скорости при бесконечном разведении, т. е. w⁰_∞ = ez_i/LДвижение ионной атмосферы можно представить себе как движение шара радиусом 1/χ в вязкой среде. Тогда по закону Стокса коэффициент пропорциональности для ионной атмосферы

L_{ион. атм} = 6πη(1/χ)

и абсолютная скорость движения ионной атмосферы (при grad Е = 1)

В этом уравнении, как и в простой гидродинамической теории, η есть динамическая вязкость чистого растворителя. Далее принято, что закон Стокса применим к движению ионов, а ионная атмосфера симметрична, т. е. релаксационный эффект несущественно искажает ее форму.

Движение ионной атмосферы будет уменьшать абсолютную скорость движения i-го иона, и его реальная скорость при данной концентрации выразится формулой:

Поскольку λ_э = F (w⁰₊ + w⁰_–), мы можем записать для бинарного 1 — 1-валентного электролита

или

Подставив в эту формулу значение χ, получим:

Таким образом, электрофоретический эффект снижает эквива-лентную электрическую проводимость пропорционально корню квадратному из концентрации электролита.

Релаксационный эффект не может быть рассчитан столь просто. Поэтому ограничимся указанием, что и этот эффект приводит к снижению λ_э также пропорционально корню квадратному из концентрации.

Общее уравнение изменения эквивалентной электрической проводимости с концентрацией для 1 — 1-валентного электролита имеет вид:

где

Уравнение для электрической проводимости выводится фактически на основе тех же предпосылок, что и уравнение первого приближения для коэффициента активности. Поэтому следует ожидать, что оно применимо к очень разбавленным растворам.

Примечательной особенностью теории является не только то, что она позволила получить открытую ранее опытным путем зависимость λ_э от С, но и дала возможность правильно рассчитывать углы наклона зависимостей λ_э — 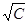, не вводя в расчеты ни одного эмпирического коэффициента. Представленные на рис. 5.13 зависимости эквивалентной электрической проводимости от корня квадратного из концентрации показывают при малых концентрациях хорошее совпадение теории с опытом. Область этих концентраций зависит от природы растворенного вещества и растворителя. Для водных растворов 1 — 1-валентных электролитов уравнение очень хорошо согласуется с опытом при концентрациях, не превышающих 2— 4∙10^–3 кмоль/м³.

Не мгновенное образование ионной атмосферы вокруг центрального иона является причиной двух эффектов, предсказанных теорией и впоследствии

Рис. 5.13. Проверка уравнения Дебая — Хюккеля — Онзагера:

точки — опытные данные; прямые рассчитаны по уравнению.

Рис. 5.14. Эффект Вина для сильных электролитов:

1 — MgSO₄ в воде; 2 — КI в ацетоне.

Pис. 5.15. Эффект Вина для слабых электролитов:

1 — LiBr в ацетоне; 2 — СН₃СООН в воде.

обнаруженных. Первый эффект, предсказанный в 1928 г. Дебаем и Фалькенгагеном, относится к измерению сопротивления переменным током очень большой частоты. При этом за полпериода тока ион успевает пройти столь малое расстояние, что симметрия ионной атмосферы, практически не нарушается и релаксационное торможение исчезает. А это приводит к тому, что измеренное на очень больших частотах сопротивление электролита уменьшается по сравнению с измерением на средних частотах и, следовательно, эквивалентная электрическая проводимость возрастает. В соответствии с общими теоретическими представлениями обнаружено, что эффект Дебая и Фалькенгагена больше в тех случаях, когда медленнее образуется ионная атмосфера.

Второй эффект относится к измерению сопротивления раствора электролита постоянным током высокого напряжения. В поле очень высокой напряженности ионы могут приобретать столь большую скорость, что ионная атмосфера не будет успевать образовываться и. ионы будут двигаться как бы в голом виде. В этих условиях, естественно, исчезнет не только релаксационное, но и электрофо-ретическое торможение и скорость движения иона станет равной w_i∞. Возрастание электрической проводимости сильных электролитов в поле очень высокой напряженности до значения, отвечающего бесконечному разведению, называется, по имени первооткрывателя этого явления, первым эффектом Вина. Экспериментальное обнаружение эффекта Вина весьма непросто, так как при таких напряженностях поля электролит легко разогревается, что увеличивает его электрическую проводимость. Поэтому приходится пользоваться кратковременными импульсами тока, длящимися всего несколько миллионных долей секунды. Результаты, полученные Вином для некоторых солей, представлены на рис. 5.14.

Увеличение эквивалентной электрической проводимости с напряженностью электрического поля Вин обнаружил также для слабых электролитов. В этом случае скорость w_i∞ не достигается.

Наоборот, с ростом напряженности, по крайней мере в доступном интервале градиентов напряженности, электрическая проводимость возрастает в степени больше первой (рис. 5.15). Причиной эффекта Вина в слабых электролитах является в основном дополнительная диссоциация электролита в электрическом поле очень высокой напряженности (второй эффект Вина).

ТЕОРИЯ ЭЙРИНГА

Согласно Эйрингу, движение ионов под действием электрического поля происходит таким образом, что они перескакивают из одного положения равновесия, в другое. В каждом из положений равновесия в «вакансии» растворителя ион обладает минимумом потенциальной энергии. Для того, чтобы мог произойти перескок в соседнее положение равновесия, иону должна быть сообщена некоторая добавочная энергия — энергия активации. Добавочная энергия затрачивается на разрыв связей перескакивающего иона с окружающими его частицами или, как говорят, на преодоление потенциального барьера.

При отсутствии электрического поля перескоки из -одного состояния равновесия в другое происходят беспорядочно и в среднем энергия активации для перескока в любом направлении одна и та же. Этот случай изображен на рис. 5.16, а, на котором по оси ординат отложена потенциальная энергия U иона, а по оси абсцисс— направление х. При перескоке иона в «прямом направлении», например из положения А в положение В, энергия активации будет А₀. При перескоке нона в «обратном направлении» (из положения В в положение А) энергия активации тоже будет а₀. Однако при наложении электрического поля частоты прямых и обратных перескоков уже не будут равны друг другу. Частота перескоков по градиенту потенциала будет больше, чем против него. Электрическое поле как бы сообщает иону, перескакивающему в направлении градиента поля, дополнительную энергию ΔU (рис. 5.16, б), а это эквивалентно подъему кривой потенциальной энергии иона и снижению энергии активации А. Как видно из рисунка, значение энергии активации при прямом перескоке составит:

А_пр = а₀ + αΔU – ΔU = A₀ – (1 – α)ΔU

Рис. 6.16. Схема потенциальных кривых.

Перескок иона против градиента потенциала будет сопровождаться повышением энергии активации, ибо в этом случае поле как бы уменьшает потенциальную энергию иона, находящегося в положении В, на такое же значение ΔU. Следовательно, в случае обратного перескока для энергии активации при наличии поля можем написать (рис. 5.16, в):

А_обр = А₀ + ΔU – αΔU = A₀ + (1 – α)ΔU

Согласно формуле Аррениуса, скорость w процесса, т. е. число перескоков в единицу времени, пропорциональна числу ионов в данном объеме (п) и экспоненциальному фактору:

Следовательно, скорость перескока ионов в прямом направлении

в обратном

При этом ΔU относят к одному молю ионов и предполагают, что заметного изменения концентрации растворенного вещества вдоль координаты движения не происходит, т. е., что движение ионов не создает концентрационного градиента и что коэффициент активности остается постоянным и может быть объединен с константой.

Скорость движения ионов будет равна разности скоростей перескока в прямом и обратном направлениях: w = w_пр – w_обр.

Определим теперь п. Обозначим через S поверхность, перпендикулярную направлению тока. Тогда объем, в котором все ионы могут перескочить из одного положения равновесия в другое, будет равен x’S. Концентрацию ионов в единице объема обозначим

через С (кмоль/м³). Тогда число ионов в объеме составит CNx'S∙10³ (где N — число Авогадро). Приняв S = 1 м², получим:

Разложим экспоненты в ряд и ограничимся первыми двумя членами разложения:

или

Так как потенциальный барьер обычно симметричен, то α = 0,5 и

Но

Здесь ze — заряд иона; dE/dx — градиент потенциала. Следовательно, х'(dE/dx) — падение напряжения по длине х', и все произведение — суть электрическая работа, которую нужно затратить для повышения потенциальной энергии моля иона, совершающего перескок из одного положения в другое.

Подставим это выражение в уравнение скорости:

Обозначим (x’)²k’ = D. Тогда для любого i-го сорта ионов:

Введя обозначение

получим

или при градиенте потенциала, равном единице

Здесь w_i⁰— линейная скорость движения ионов (м/с) при градиенте потенциала, равном единице. Действительно, поскольку w_iотносится к 1 м³, то w_i⁰есть объем, из которого в единицу времени мигрируют все содержащиеся в нем ионы. А таких ионов СN∙10³. Учитывая, что w_i⁰F = l_i, для подвижности иона получаем выражение:

l_i = D_iz_iF²/RT

Таким образом, теория Эйринга на основе иных исходных положений приводит к тем же уравнениям, что и простая гидродинамическая теория.