Уравнения и граничные условия для источников

Гальванического типа

В соответствии с эквивалентной электрической схемой двой­ного электрического слоя разность потенциалов между его об­кладками будет

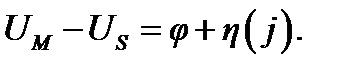(2.8)

Если граничную поверхность совместить с внешней обкладкой двойного слоя, то среда, в которой необходимо рассчитывать электрическое поле, не будет содержать каких-либо связанных или свободных зарядов и потенциал будет удовлетворять урав­нению Лапласа

ΔU = 0.

При этом электрохимические явления, происходящие на гра­нице раздела металл-морская среда, учитываются посредством граничного условия. Поскольку 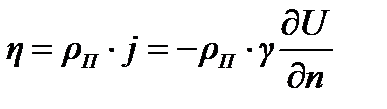из (2.8), получим

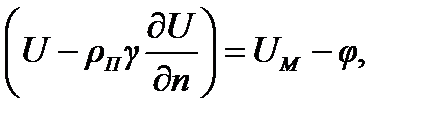
где γ - удельная электрическая проводимость воды, См/м;

п - внешняя нормаль к поверхности S.

2.3. Приближённый расчёт полных токов

Гальванических источников

При расчёте полных токов гальванических источников разде­ляют гальванические пары и многоэлектродные системы. Знание полных токов позволяет определить интенсивность источников гальванического типа и найти, например, суммарные коррозион­ные потери металла, работающего в анодном режиме. Послед­нее, в основном, относится к определению износа протекторов и анодов систем электрохимической защиты. Для оценки уровней локальной коррозии необходим, как правило, расчёт распределе­ния плотности тока по омываемым поверхностям.

2.3.1. Расчёт гальванической пары

Гальванической парой называются два разнородных металла (электрода), погружённые в электролит и соединённые между со­бой по внутренней цепи. Гальваническая пара всегда считается электронейтральной, то есть, сколько тока стекает с анодного электрода, столько же притекает к катодному.

В гальванической паре электрод с более электроотрицатель­ным стационарным потенциалом всегда является анодом, поэто­му задачей расчёта является только определение полного тока гальванопары.

2.3.2. Аналитический расчёт гальванической пары

Аналитический расчёт тока гальванической пары выполняется при следующих допущениях: плотность тока на поверхности каж­дого из электродов считается постоянной; удельные поляризаци­онные кривые металлов линейны.

Указанные допущения позволяют заменить гальваническую па­ру эквивалентной электрической схемой, показанной на рис. 2.11.

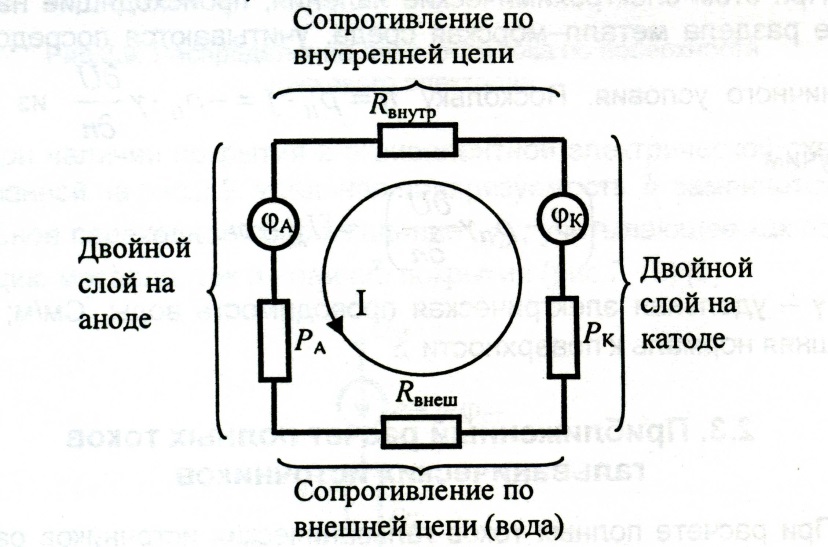
Рис.2.11. Эквивалентная схема гальванической пары

В соответствии с данной эквивалентной электрической схемой Закон Ома для гальванической пары выражается формулой

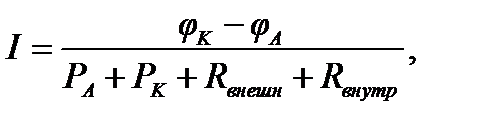(2.9)

где φ_A и φ_K — стационарные электрохимические потенциалы анода и катода;

φ_K ‒ φ_A — ЭДС;

Р_A и Р_K — полные поляризуемо­сти анода и катода;

R_внутр — внутреннее (омическое) сопротивление;

R_внешн — сопротивление непосредственно по воде (общепри­нятое название ‒ сопротивление растеканию).

2.3.3. Графический расчёт гальванической пары

Графический расчёт гальванопар может быть выполнен и для нелинейных поляризационных кривых металлов. Распределение плотности тока на анодной и катодной поверхностях считается равномерным.

На первом шаге удельные поляризационные кривые металлов перестраивают в полные анодную и катодную поляризационные кривые, а затем строится суммарная вольт-амперная характери­стика гальванической пары. Порядок построения поясняется на рис. 2.12.

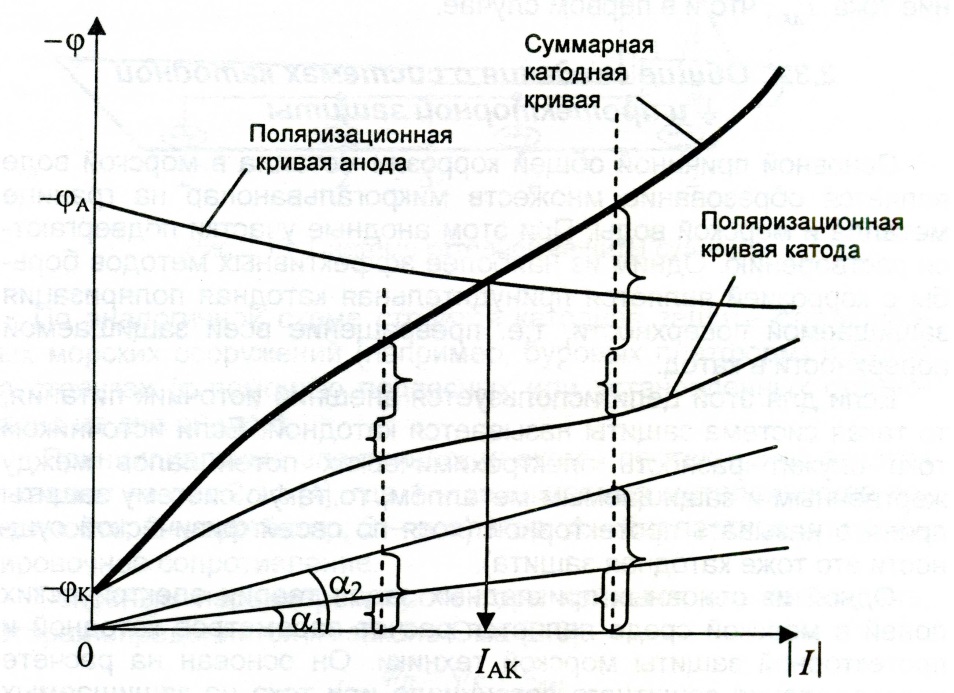
Рис. 2.12. Графический расчёт гальванической пары

Поскольку ток во всей цепи гальванической пары один и тот же, то сложение линейных зависимостей для сопротивлений внешней и внутренних цепей с поляризационными кривыми осу­ществляется по напряжению. На рис. 2.12 вольт-амперные харак­теристики омических сопротивлений сложены по напряжению с катодной кривой. В результате получена суммарная катодная кривая, точка пересечения которой с анодной кривой и определя­ет ток гальванической пары. При этом

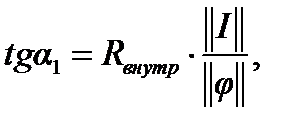
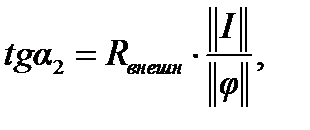
где 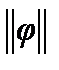и 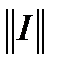— масштабы потенциала и тока.

Замечание. Вместо суммарной катодной кривой можно по­строить суммарную анодную кривую. При этом построение долж­но идти посредством вычитания соответствующих напряжений на омических сопротивлениях из анодной кривой, тогда точка пере­сечения суммарной анодной кривой с катодной даст то же значе­ние тока I_AK, что и в первом случае.