Уравнение мембранного потенциала

Предположим, что, как и в рассмотренном ранее случае (см. 5.2), имеется граница раздела растворов одного и того же электролита разных концентраций. Но отличие состоит в том, что эта граница способна пропускать не все присутствующие в электролите сорта ионов, а только некоторые из них. Таким образом, граница раздела является полупроницаемой. Такую границу можно создать, если растворы разделить мембраной, обладающей избирательной пропускной способностью. Через мембрану начнется диффузия, но не электролита в целом, а только тех частиц (ионов, молекул), которые способны через нее проникать.

Непроницаемость мембраны для некоторых сортов ионов может быть обусловлена как тем, что их размеры больше диаметра пор мембраны, так и тем, что определенные сорта ионов будут отталкиваться зарядом мембраны.

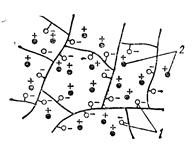
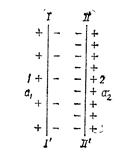
Рис. 6.13. Схема матрицы катионита:

1 — ионообменные группы; 2 — обменивающиеся катионы (противоионы).

Рис. 6.14. Схема процессов, происходящих на границе раздела мембрана — раствор.

Мембраны, обладающие ионной избирательностью, называются ионообменными или ионитовыми мембранами. Если мембраны пропускают катионы, они называются катионообменными (катио-нитовыми), если анионы, — анионообменными (анионитовыми).

Допустим, что растворы одного и того же электролита разной концентрации разделены катионитовой мембраной, матрица которой схематично представлена на рис. 6.13. Линии обозначают образованную посредством гомеополярных связей молекулярную решетку, которая содержит ионообменные группы 1, в данном случае отрицательные. Противоионы 2, несущие положительный заряд, могут свободно перемещаться в электролите, наполняющем матрицу, и могут обмениваться на другие положительные ионы.

Рассмотрим явления, происходящие на границе раздела катио-нитовая мембрана — раствор, содержащий катионы, по отношению к которым избирательна данная мембрана. Пусть I I’ и II II’ (рис. 6.14) — проекции поверхностей катионитовой мембраны, соприкасающейся соответственно с растворами 1 (активность a₁) и 2 (активность а₂), причем а₁ > а₂. Допустим, что активность катионов в мембране выше, чем в каждом из растворов. Тогда после погружения мембраны в раствор начнется переход катионов из мембраны в растворы, вследствие чего поверхность мембраны со стороны растворов будет заряжаться положительно, а на внутренней поверхности появится избыток отрицательных зарядов. Так как а₁ > > а₂, то вероятность выхода катионов в раствор с поверхности I I’ меньше, чем с II II’, что отражено на рис. 6.14 различной концентрацией зарядов на этих поверхностях.

Таким образом, на каждой из границ раздела катионитовая мембрана — раствор появится разность электрических потенциалов (скачок потенциала), которая будет тормозить переход катионов из мембраны в раствор и ускорять переход катионов из раствора на поверхность мембраны., В момент установления равновесия скорости этих переходов сравняются и на каждой границе раздела установится равновесный скачок потенциала.

Определим сначала скачок потенциала па границе раздела по- верхность мембраны I I’ — раствор 1. При равновесии электрохимические потенциалы катиона в растворе и на поверхности мембраны равны, т. е.

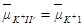
Подставляя выражения для электрохимического потенциала, получим:

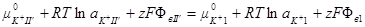
Отсюда определяем скачок потенциала на границе раздела мембрана — раствор, который называется потенциалом Доннана (φ_D):

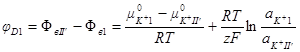
Так как 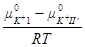– величина постоянная, то

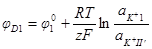
Аналогично получаем выражение для скачка потенциала, возникающего на границе раздела мембрана —раствор 2

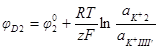
Эти потенциалы являются межфазными потенциалами, следовательно, непосредственно не могут быть ни измерены, ни рассчитаны.

Алгебраическая сумма скачков потенциалов на обеих поверхностях мембраны называется мембранным потенциалом. Учитывая, что скачки потенциала на обеих границах направлены противоположно друг другу, мембранный потенциал можно выразить следующим уравнением:

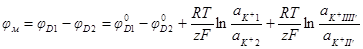
Если обе поверхности мембраны совершенно тождественны по своим физико-химическим свойствам, то

φ₁⁰ = φ₂⁰ и ≈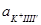

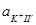
Тогда уравнение для мембранного потенциала будет иметь вид:

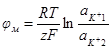
Если же поверхности мембраны не одинаковы по физико-химическим свойствам, то

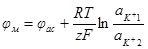
аде φ_ас – так называемый потенциал асимметрии, равный

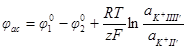
Потенциал асимметрии, учитывающий неоднородность поверхностей мембраны, является величиной постоянной и индивидуальной для каждой мембраны.

Поскольку активности а₁ и a₂ в растворах неодинаковы, то по условиям равновесия должны быть различны и концентрации катионов в поверхностных слоях мембраны, непосредственно прилегающих к этим растворам. Следовательно, внутри мембраны должен существовать некоторый градиент концентрации, а значит, и какая-то (обычно очень незначительная) диффузия, приводящая к возникновению диффузионного потенциала внутри мембраны. Принимая это во внимание, уравнение для мембранного потенциала, возникающего при разделении двух растворов различной концентрации катионитовой мембраной, в общем виде записываем так:

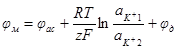
Если два раствора различной концентрации разделены анионо-обменной мембраной, то и в этом случае возникает мембранный потенциал. Уравнение для него может быть получено аналогичным образом, только нужно учесть, что переносятся не положительно, а отрицательно заряженные частицы. Уравнение для мембранного потенциала анионитовой мембраны будет иметь вид:

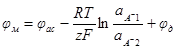
Здесь , 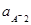— активности аниона в растворе 1 и 2, причем > .

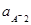На основе полупроницаемых мембран, обладающих повышенной (практически полной) избирательностью по отношению к определенному сорту ионов, созданы мембранные или так называемые ионоселективные электроды. Мембраны, используемые в ионоселективных электродах, подразделяются на три главных типа: твердые ионитовые, жидкие ионитовые и мембраны из нейтральных агентов, связывающих ионы.

В ионоселективных электродах мембрана, как правило, разделяет два раствора — внутренний и внешний, причем активность ионов, к которым мембрана избирательна, во внутреннем растворе постоянна.