Какими показателями могут быть охарактеризованы электрические свойства дисперсных систем?

Электрические свойства дисперсных систем характеризуются тремя показателями – зарядом, потенциалом и подвижностью.

Напомним, что подвижность в электрическом поле (электрофоретическая подвижность) – это скорость движения частиц в поле с единичной напряженностью:

, .

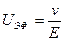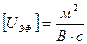Напряженность электрического поля в той или иной точке – эта сила, действующая на единичный положительный заряд:

, .

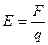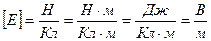Для сферических частиц подвижность можно определить как:

,

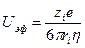где z_i – заряд частиц; r_i – размер частиц.

Подвижность определяют, измерив скорость движения частиц, по следующей формуле:

, ,

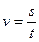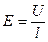где U – разность потенциалов между точками на расстоянии l.

В то время как напряженность является силовой характеристикой поля, потенциал служит энергетической характеристикой.

Пусть поле создано неким зарядом Q. Потенциал поля в некоторой точке – это работа по перемещению единичного положительного заряда из бесконечности в данную точку поля:

.

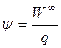Если Q > 0, то при приближении заряда q = +1 из бесконечности в некоторую точку поля работа совершается против системы, т. е. Ψ > 0. Напротив, если Q < 0, то при указанном перемещении работа совершается самой системой, откуда Ψ < 0. Следовательно, знак потенциала совпадает со знаком полеобразующего заряда. Потенциал поля точечного заряда равен:

,

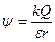где к – коэффициент пропорциональности в законе Кулона; Q – заряд; ε – диэлектрическая проницаемость среды; r – расстояние до точечного заряда.

А если частица, создающая поле, является не бесконечно малой точкой, а равномерно заряженной сферой? Внутри сферы все точки имеют один и тот же потенциал, равный потенциалу на поверхности сферы. Вне сферы создаваемый ею потенциал убывает с ростом расстояния от центра сферы. Следовательно, для сферы формула приобретает вид:

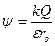при r_o ≥ r и 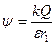, если r_o ≤ r,

где r_o – постоянная величина, радиус сферы, который наряду с зарядом Q определяет потенциал во всех точках внутри сферы.

Вопросы и задания для самоконтроля знаний по материалу 12-й лекции

1 Сформулируйте

Знакомимся с основными понятиями физической химии (для курсантов военного факультета)

Повторяем курс физической химии (для студентов химического факультета)

1. ...............

ЛЕКЦИЯ 13

«Впервые представление об образовании двойного электрического слоя было высказано Г. Квинке (1859 г) и развито в работах Г. Гельмгольца (1879 г), который предложил первую модель двойного электрического слоя. Основы современной теории двойного электрического слоя были разработаны О. Штерном. Модификацию его теории для улучшения согласия по емкости ДЭС проводили Дж. Филпот, Л. Фрумкин, Дж. Биккерман, Д. Грэхем. Уточнения касались учета различных свойств катионов и анионов, объема ионов, степени их гидратации в адсорбционном слое»

....

Современная модель строения мицеллы учитывает тот факт, что противоионы располагаются в два слоя – плотный и диффузный, и что поверхностью скольжения частицы в растворе является граница между этими слоями. В связи с этим рассматривается три заряженные сферы. Первая – поверхность ядра с параметрами Q и r_я. Вторая сфера – поверхность коллоидной частицы с радиусом r_к и зарядом -Q + x (x – общий заряд тех противоионов, которые остаются в диффузном слое). Третья сфера – это условная поверхность, к которой можно «привязать» заряд диффузной части противоионов (-x). Для оценки эффективного радиуса этой поверхности (точнее, величины d = r_м - r_к) вполне применима теория Дебая-Хюккеля, согласно которой d можно найти по уравнению:

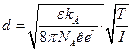
Отсюда следует, что эффективная толщина диффузного слоя противоионов, а значит и эффективный радиус мицеллы зависят от ионной силы раствора (I) и от температуры (T): размеры d и r_м = r_к + d увеличиваются при нагревании и снижении ионной силы. Например, если T = 300 К и I = 0,1 моль/дм³, то d ≈ 10^-9 м = 1 нм; если при той же температуре I = 0,01 моль/дм³, то d ≈ 3,1 нм

Итак, учитывая три сферы, рассчитаем результирующий потенциал на поверхности каждой из них.

Потенциал на поверхности ядра; теперь мы его обозначим как φ-потенциал (фи-потенциал):

.

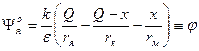Потенциал на поверхности коллоидной частицы; теперь именно он обозначается как ζ-потенциал (дзета-потенциал):

.

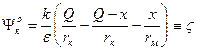Очевидно, что ζ < φ.

Наконец, потенциал на поверхности радиуса r_м равен нулю – мицелла в целом электронейтральна:

.

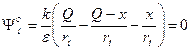Преобразуем выражение для дзета-потенциала:

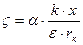, где 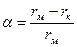, x = Q - q_пл,

где q_пл – заряд противоионов в плотном слое.

В системе SI 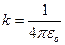, где ε_o = 8,85∙10^-12 Ф/м.

С учетом этого ;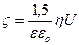

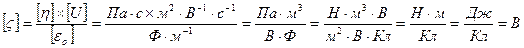
В рамках современной теории строения ДЭС получили объяснение электрокинетические и электрокапиллярные явления, а также проблемы строения и устойчивости коллоидных частиц лиофобных золей. При относительном движении жидкой и твердой фаз их плоскость скольжения лежит на некотором расстоянии от твердой фазы. Слой жидкой фазы толщиной в 2-3 молекулы при движении фаз остается неподвижным вместе с твердой фазой. Иными словами, непосредственно у поверхности коллоидной частицы образуется так называемый адсорбционный слой, который включает не только потенциалопределяющие ионы (ПОИ), но и часть противоионов, которые в обычных условиях считаются неподвижными и при движении твердой фазы перемещаются вместе с ней. Неподвижный адсорбционный слой содержит далеко не все ионы, а лишь определенную их часть, которая не в состоянии целиком компенсировать заряд твердой поверхности, а способные лишь понизить его. Иными словами, в адсорбционном неподвижном слое в результате взаимодействия положительных и отрицательных зарядов остается ненейтрализованным некоторый потенциал, который является частью общего потенциала поверхности твердой фазы.