Квантово-механическая модель атома

Современная модель атома является развитием планетарной модели. Согласно этой модели, ядро атома состоит из положительно заряженных протонов и не имеющих заряда нейтронов и окружено отрицательно заряженными электронами. Однако представления квантовой механики не позволяют считать, что электроны движутся вокруг ядра по сколько-нибудь определённым траекториям (неопределённость координаты электрона в атоме может быть сравнима с размерами самого атома).Химические свойства атомов определяются конфигурацией электронной оболочки и описываются квантовой механикой. Положение атома в таблице Менделеева определяется электрическим зарядом его ядра (то есть количеством протонов), в то время как количество нейтронов принципиально не влияет на химические свойства; при этом нейтронов в ядре, как правило, больше, чем протонов (см.: атомное ядро). Если атом находится в нейтральном состоянии, то количество электронов в нём равно количеству протонов. Основная масса атома сосредоточена в ядре, а массовая доля электронов в общей массе атома незначительна (несколько сотых процента массы ядра).Массу атома принято измерять в атомных единицах массы, равных ¹⁄₁₂ от массы атома стабильного изотопа углерода ¹²C.

Принцип неопределённости Гейзенбе́рга (или Га́йзенберга) в квантовой механике — фундаментальное неравенство (соотношение неопределённостей), устанавливающее предел точности одновременного определения пары характеризующих квантовую систему физических наблюдаемых (см. физическая величина), описываемых некоммутирующими операторами (например, координаты и импульса, тока и напряжения, электрического и магнитного поля). Соотношение неопределенностей^{[* 1]} задаёт нижний предел для произведения среднеквадратичных отклонений пары квантовых наблюдаемых. Принцип неопределённости, открытый Вернером Гейзенбергом в 1927 г., является одним из краеугольных камней квантовой механики.

Краткий обзор

Соотношения неопределённостей Гейзенберга являются теоретическим пределом точности одновременных измерений двух некоммутирующих наблюдаемых. Они справедливы как для идеальных измерений, иногда называемых измерениями фон Неймана, так и для неидеальных измерений.^{[* 2]}

Согласно принципу неопределённостей у частицы не могут быть одновременно точно измерены положение и скорость (импульс)^{[* 3]}. Принцип неопределённости уже в виде, первоначально предложенном Гейзенбергом, применим и в случае, когда ни одна из двух крайних ситуаций (полностью определенный импульс и полностью неопределенная пространственная координата — или полностью неопределенный импульс и полностью определенная координата) не реализуется.

Пример: частица с определённым значением энергии, находящаяся в коробке с идеально отражающими стенками; она не характеризуется ни каким-либо определённым «положением» или пространственной координатой (волновая функция частицы делокализована на всё пространство коробки, то есть ее координаты не имеют определенного значения, локализация частицы осуществлена не точнее размеров коробки), ни определённым значением импульса (учитывая его направление!^{[* 4]}).

Соотношения неопределённостей не ограничивают точность однократного измерения любой величины (для многомерных величин тут подразумевается в общем случае только одна компонента). Если её оператор коммутирует сам с собой в разные моменты времени, то не ограничена точность и многократного (или непрерывного) измерения одной величины. Например, соотношение неопределённостей для свободной частицы не препятствует точному измерению её импульса, но не позволяет точно измерить её координату (это ограничение называется стандартный квантовый предел для координаты).

Соотношение неопределенностей в квантовой механике в математическом смысле есть непосредственное прямое следствие некоего свойства преобразования Фурье^{[* 5]}.

Существует точная количественная аналогия между соотношениями неопределённости Гейзенберга и свойствами волн или сигналов. Рассмотрим переменный во времени сигнал, например звуковую волну. Бессмысленно говорить о частотном спектре сигнала в какой-либо момент времени. Для точного определения частоты необходимо наблюдать за сигналом в течение некоторого времени, таким образом теряя точность определения времени. Другими словами, звук не может одновременно иметь и точное значение времени его фиксации, как его имеет очень короткий импульс, и точного значения частоты, как это имеет место для непрерывного (и в принципе бесконечно длительного) чистого тона (чистой синусоиды). Временно́е положение и частота волны математически полностью аналогичны координате и (квантово-механическому) импульсу частицы. Что совсем не удивительно, если вспомнить, что 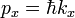, то есть импульс в квантовой механике — это и есть пространственная частота вдоль соответствующей координаты.

В повседневной жизни мы обычно не наблюдаем квантовую неопределённость потому, что значение 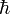чрезвычайно мало, и поэтому соотношения неопределенностей накладывают такие слабые ограничения на погрешности измерения, которые заведомо незаметны на фоне реальных практических погрешностей^{[* 6]} наших приборов или органов чувств.

5. Волнова́я фу́нкция, или пси-функция 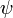— комплекснозначная функция, используемая в квантовой механике для описания чистого состояния системы. Является коэффициентом разложения вектора состояния по базису (обычно координатному):

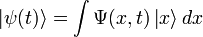
где 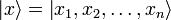— координатный базисный вектор, а 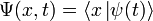— волновая функция в координатном представлении.

Физический смысл волновой функции заключается в том, что согласно копенгагенской интерпретации квантовой механики плотность вероятности нахождения частицы в данной точке конфигурационного пространства в данный момент времени считается равной квадрату абсолютного значения волновой функции этого состояния в координатном представлении.

Ква́нтовое число́ в квантовой механике — численное значение какой-либо квантованной переменной микроскопического объекта (элементарной частицы, ядра, атома и т. д.), характеризующее состояние частицы. Задание квантовых чисел полностью характеризует состояние частицы.

Некоторые квантовые числа связаны с движением в пространстве и характеризуют вид волновой функции частицы. Это, например, радиальное (главное) ( 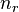), орбитальное ( 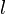) и магнитное ( 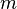) квантовые числа электрона в атоме, которые определяются как число узлов радиальной волновой функции, значение орбитального углового момента и его проекция на заданную ось, соответственно.

Некоторые другие квантовые числа никак не связаны с перемещением в обычном пространстве, а отражают «внутреннее» состояние частицы. К таким квантовым числам относится спин и его проекция. В ядерной физике вводится также изоспин, а в физике элементарных частиц появляется цвет, очарование, прелесть (или красота^[1]) и истинность.

6.Порядок заполнения энергетических уровней : Для описания состояния электрона в атоме используются 4 квантовых числа (n,l,m,s). Первые три соответствуют трем степеням свободы электрона в трехмерном пространстве, а четвертое соответсвует вероятности вращения электрона вокруг воображаемой собственной оси. Квантовые числа:

1. “n” – главное квантовое число. Характеризует уровень энергии электрона в поле атома (удаленность от ядра). Математическая зависимость энергии связи с ядром: E_a=-13,6/n² Эв, n=1,2,… Для реальных элементов n=1,…,7. n=номеру периода.

2. “l” – орбитальное квантовое число. Характризует тип подуровня (форма электронного облака). l=0,1,2,…,(n-1). Обозначается буквами. При этом l=0 соответствует s, 1-p, 2-d, 3-f, 4-q, 5-h.

3. “m” – магнитное квантовое число. Характеризует пространственное расположение орбитали. m= 0,  1,  2,…,  l. Cумма орбиталей на подуровне:  =2l+1.

4. “s” – спиновое квантовое число. Характеризует вероятность вращения электрона вокруг своей оси в двух противоположенных направлениях. s= 1/2. “+” – по часовой стрелке, “-“ – против часовой стрелке. Вращение сообщает электрону собственный магнитный момент, который называется спином электрона.

5. Принцип Паули (запрет): у атомов, имеющих больше одного электрна не может быть двух электронов с одинаковыми значениями всех четырех квантовых чисел. Или так: на одной орбитали могут находится только два электрона, причем с противоположенными спинами.

6. Принцип минимума энергии: последовательное заполенние электронов в атоме должно отвечать как минимому энергии самого электрона, так и минимому энерги атома в целом. Или так: минимум энергии соответствует максимому устойчивости. Заполение идет в соответсвии с уравнением энергии орбитали: ns<(n-1)d (n-2)f<np. На внешнем уровне не может быть более 8 электронов.

7. Правило Клечковского: сначала заполняются те подуровни, сумма n+l которых наименьшая. Если для двух подуровней сумма n+l равна, то сначала заполняется подуровень с меньшим n.

8. Правило Хунда: в основном (невозбужденном) состоянии атома на подуровнях np, nd и nf всегда имеется максимальное количество неспаренных электронов (максимальный неспаренный спин).

9. Подуровни p, d и f состоят из нескольких орбиталей, энергия которых одинакова, поэтому эти подуровни называются “вырожденными”: p подуровень вырожден трехкратно, d пятикратно и f семикратно. Для электронов этих подуровней соблюдается правило Хунда.

10. Валентность – способность образовывать химические связи.

11. Основное состояние – состояние с минимальной энергией, т.е электроны находятся ближе к ядру.

12. Возбужденное состояние – состояние, при котором все или часть электронов в атоме распарены и находятся на подуровне с большей энергией, т.е дальше от ядра.

13. Максимальная валентность наблюдается в возбужденном состоянии и как правило совпадает с номером группы, в которой находится элемент.

Сте́пень окисле́ния (окислительное число, формальный заряд) — вспомогательная условная величина для записи процессов окисления, восстановления и окислительно-восстановительных реакций, численная величина электрического заряда, приписываемого атому в молекуле в предположении, что электронные пары, осуществляющие связь, полностью смещены в сторону более электроотрицательных атомов.