Двойной слой на твердых электродах

При измерении емкости двойного электрического слоя на твердых электродах (Д. И. Лейкис, А. Н. Фрумкин) возникают трудности, одной из которых является чрезвычайно узкая область идеальной поляризуемости. Поэтому электрод обычно ведет себя не как идеально поляризуемый, и измеряемый импеданс, помимо емкости двойного электрического слоя, содержит другие составляющие. Вторая трудность — зависимость измеряемой емкости двойного слоя от частоты переменного тока, что главным образом связано с шероховатостью поверхности твердых электродов. При тщательной полировке поверхности частотная зависимость емкости может быть сведена к небольшой величине, составляющей 3—5% в интервале частот 0,1 — 10 кГц. В настоящее время наиболее точные результаты получены в основном на монокристаллических или полированных электродах из металлов, плохо адсорбирующих водород (Pb, Bi, Cd, Tl, Sb, Sn, Ag), при отсутствии на их поверхности оксидных пленок. Строение двойного слоя на твердых электродах соответствует представлениям Грэма. Емкость двойного слоя может быть представлена как емкость двух последовательно соединенных конденсаторов

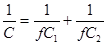
где С — емкость, отнесенная к единице видимой поверхности; С₁ и С₂ — емкости плотного и диффузного двойного слоя, отнесенные к единице истинной поверхности; f — коэффициент, учитывающий шероховатость поверхности и неточность ее определения (для ртутного электрода f = 1).

Последнее уравнение позволяет определить f из зависимости 1/С от 1/С₂, которую рассчитывают по теории Гуи — Чапмена. Для ртутного электрода эта зависимость имеет единичный наклон. На хорошо полированных и освобожденных от оксидов электродах зависимость 1/С от 1/С₂ также близка к единице (примерно 1,05 — 1,30), что свидетельствует о применимости теории Грэма к твердым электродам.

В разбавленных растворах, как и на ртутном электроде, на зависимости С — Е наблюдается минимум емкости вблизи потенциала нулевого заряда. При этом для хорошо полированных металлов как форма кривой, так и абсолютные значения емкости удовлетворительно совпадают с полученными на ртутном электроде.

Измеренные значения потенциалов нулевого заряда по минимуму дифференциальной емкости диффузного слоя на некоторых твердых поликристаллических металлах приведены в табл. 7.1. Значение потенциала нулевого заряда зависит как от природы металла, так и от грани монокристалла. Таким образом, потенциал нулевого заряда поликристаллического электрода представляет собой некоторое усредненное значение потенциалов нулевого заряда отдельных граней, выходящих на поверхность. Из табл. 7.1 видно, что в хлоридном растворе потенциал нулевого заряда таллия отрицательнее, чем в растворе фторида натрия, что свидетельствует о специфической адсорбции аниона. Специфическая адсорбция анионов в сильной степени зависит от природы металла и проявляется в сдвиге потенциала нулевого заряда в область отрицательных значений потенциалов. В области отрицательных зарядов поверхности на твердых металлах проявляется и специфическая адсорбция катионов, которая также зависит от природы металла,

Таблица 7.1. Потенциалы нулевого заряда поверхности разных металлов в водородной шкале

Металл	Раствор, в котором производи-лось измерение, и его концентра-ция (кмоль/м3)	Ен. з	Металл	Раствор, в котором производи-лось измерение, и его концентра-ция (кмоль/м3)	Ен. з
Ag (110) Ag (100)   Ag (111) Ag (поли-кристал-лический) Сd Tl Ti Ta Ga In Zn Nb Pb Cr	NaF, 0,01 Na2SO4, 0,0025 KF, 0,001 Na2SO4, 0,0025   NaF, 0,001 NaF, 0,001 – – – NaF, 0,003 – – NaF, 0,001 –	–0,77±0,02 –0,65±0,02   –0,46±0,02 –0,67±0,03     –0,75±0,02 –0,71±0,04 –0,70 –0,70 –0,65 –0,65±0,02 –0,60 –0,60 –0,56±0,02 –0,45	Sn   Co Bi Fe Mo Ni W Hg Sb   Re Rh Ir Cu Pd Pt Au	Na2SO4, 0,00125 – KF, 0,002 – – – – NaF, 0,001 KClO4, 0,002 – – – NaF, 0,01 – – –	–0,43±0,02   0,40 –0,39±0,02 –0,35 –0,30 –0,25 –0,25 –0,19±0,01 –0,15±0,02   –0,20 0,00 0,05 0,09±0,02 0,10 0,15 0,20

В присутствии органических веществ, адсорбирующихся на твердых электродах, на зависимости С — Е появляются пики адсорбции — десорбции, высота которых закономерно зависит от концентрации поверхностно-активного вещества. Эти экспериментальные результаты указывают на то, что в строении двойного слоя на твердых электродах и на ртути нет принципиальных различий.

Исследования строения двойного слоя в неводных растворах проведены в основном на ртутном электроде вспиртах, амидах и некоторых апротонных растворителях, таких, как диметилсульф-оксид, пропиленкарбонат и ацетонитрил. Основные закономерности теории строения двойного слоя соблюдаются и в этом случае. Специфическая адсорбция анионов в сильной степени зависит от природы апротонного растворителя, что связано с изменением энергии сольватации в них анионов по сравнению с водой. Абсолютные значения дифференциальной емкости в апротонных растворителях обычно ниже, чем в воде, и не коррелируют с диэлектрической проницаемостью растворителя.

Для идеально поляризуемых электродов заряд металлической обкладки двойного слоя численно равен по абсолютному значению и противоположен по знаку заряду ионов, находящихся в электролите (заряду ионной обкладки). Если заряд определить как ко- личество электричества, которое нужно сообщить электроду при увеличении его поверхности на 1 м² для того, чтобы разность потенциалов электрод — раствор осталась постоянной, сохраняя постоянными химические потенциалы всех компонентов раствора (как заряженных, так и не заряженных), а также компонентов металлической фазы, то такой заряд является полным (или термодинамическим) зарядом q электрода. Величина его фигурирует во всех термодинамических уравнениях.

Однако в реальных условиях в зависимости от природы металла и состава раствора заряд металлической обкладки может быть иным, вследствие частичного переноса заряда при адсорбции ионов. Другим, осложняющим фактором, характерным для обратимых электродов, является перенос ионов через границу раздела фаз при изменении поверхности раздела. В обоих случаях заряд металлической обкладки будет частично компенсирован либо адсорбцией ионов, либо переходом их через границу раздела фаз. Оставшийся заряд металлической обкладки двойного слоя называется свободным зарядом поверхности электрода (q_св) и зависит от выбора модели двойного электрического слоя. Представление о полном и свободном зарядах поверхности электрода в наиболее точном виде сформулировали А. И. Фрумкин, О. А. Петрий и Б. Б. Дамаскин.

Для идеально поляризуемых электродов при отсутствии частичного переноса заряда значения полного и свободного зарядов совпадают.

Для обратимых электродов значение полного нулевого заряда не является однозначным, так как в растворе имеются компоненты (окисленная и восстановленная формы), активности которых при заданном потенциале электрода и постоянных активностях других компонентов, автоматически поддерживаются постоянными.

Так, если двойной электрический слой на обратимом электроде создается без подвода электричества извне, то для простой окислительно-восстановительной реакции Ox + e = Red имеем

q_св = (Г_Ох – A_Ox) ^F или q_св = (– Г_Red + A_Red) ^F

где Г_Ox и Г_Red — адсорбция окисленной и восстановленной формы; А_Ox и Г_Red — поверхностные активности окисленной и восстановленной формы.

Уравнение Гиббса ( 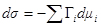) для рассматриваемого случая примет вид:

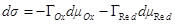
При μ_Ox = const dE = – dμ_Red/F

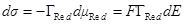
Аналогично при μ_Ox = const dE = dμ_Red/F

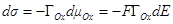
Уравнение Липпмана будет иметь вид:

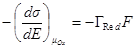или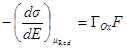

Подставляя в них выражения для свободного заряда, получим:

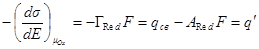
и

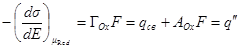
Таким образом, для обратимых электродов можно получить два уравнения Липпмана, поддерживая постоянной активность либо окисленной, либо восстановленной формы. При этом полные заряды электрода будут различны, а связь между ними выразится соотношением

q’’ – q’ = A_Ox + A_Red

Следовательно, для таких систем могут быть получены два типа электрокапиллярных кривых, которые называются электрокапиллярными кривыми первого и второго рода. Максимумы электрокапиллярных кривых отвечают потенциалу нулевого полного заряда. Эти кривые совпадают при A_Ox = A_Red = 0. В этом случае потенциал максимума соответствует потенциалу нулевого свободного заряда. Электрокапиллярные кривые первого и второго рода получили А. Н. Фрумкин, О. А. Петрий и Б. Б. Дамаскин для электродов из платиновых металлов, обратимо адсорбирующих водород.