Полиморфные или аллотропические модификации

Устойчивые модификации при более низкой температуре часто обозначают а, при более высокой 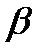, 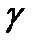так Fеα — Fе .

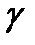Полиморфизм объясняется уменьшением энергии Гиббса. Полиморфное превращение сопровождается скачкообразным изменением всех свойств металлов или сплавов: удельного объема, теплостойкости, теплопроводности, у, магнитных свойств, химических и механических свойств.

Превращения из одной формы в другую при нагреве чистого металла сопровождаются поглощением тепла и происходят при постоянной температуре

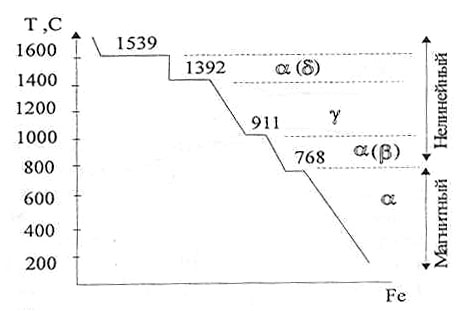
Аллотропические модификации железа

2. Твердые растворы с неограниченной растворимостью образуются при условиях:

— одинаковые типы кристаллических решеток у А и В;

— различие в атомных размерах ≤8 — 15%;

— близкое строение валентной оболочки электронов в атоме. Например, Au + Ag с ГЦК решеткой или Мо + W.

Вариант 11

1. Температурная зависимость удельного сопротивления металлических проводников. В идеальном кристалле длина свободного пробега электронов равна бесконечности, а сопротивление электрическому току равно нулю. Подтверждением данного положения является тот факт, что сопротивление чистых отожженных металлов стремится к нулю, когда температура приближается к абсолютному нулю. Свойство электрона свободно перемещаться в идеальной кристаллической решетке не имеет аналога в классической механике. Рассеяние, приводящее к появлению сопротивления, возникает в тех случаях, когда в решетке имеются дефекты строения.

В чистых металлах совершенной структуры единственной причиной, ограничивающей длину свободного пробега электронов, является тепловое колебание атомов в узлах кристаллической решетки. Электрическое сопротивление металла, обусловленное тепловым фактором, обозначим через ρт. Совершенно очевидно, что с ростом температуры увеличиваются амплитуды тепловых колебаний атомов и связанные с ними флуктуации периодического поля решетки. А это, в свою очередь, усиливает рассеяние электронов и вызывает возрастание удельного сопротивления. .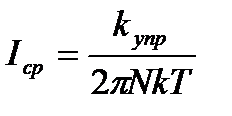

Это отношение не выполняется при низких температурах. Дело в том, что с понижением температуры могут уменьшаться не только амплитуды тепловых колебаний атомов, но и частоты колебаний. Поэтому в области низких температур рассеяние электронов тепловыми колебаниями узлов решетки становится неэффективным.

Температура Дебая определяет максимальную частоту тепловых колебаний, которые могут возбуждаться в кристалле:

ΘD = hV_mах/k

Эта температура зависит от сил связи между узлами кристаллической решетки и является важным параметром твердого тела.

При переходе из твердого состояния в жидкое у большинства металлов наблюдается увеличение удельного сопротивления приблизительно в 1,5 - 2 раза, хотя имеются и необычные случаи: у веществ со сложной кристаллической структурой, подобных висмуту и галлию, плавление сопровождается уменьшением р.

2. Определение плотности металлов и сплавов методом гидростатического взвешивания.Плотностью металла 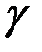называется масса единицы объема этого металла Зная массу m и объем V металла, можно вычислить . .

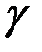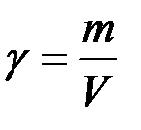Определение плотности металла сводится к определению массы и объема испытуемого образца. Масса измеряется при помощи аналитических весов. Что касается определения объема, то его можно производить двумя методами: пикнометрически и гидростатически.

Точным методом, пригодным для исследовательских целей, является метод гидростатический. Он основан на законе Архимеда.

Испытуемый образец дважды взвешивается на аналитических весах, как обычно, на воздухе и будучи погруженным в какую-либо жидкость. Если масса образца на воздухе Р, а в жидкости Q то Р - Q равняется массе вытесненной жидкости. Зная плотность этой жидкости d, можно вычислить ее объем, вытесненный образцом, или, другими словами, объем образца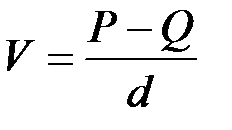

Плотность металла можно рассчитать, зная массу и объем элементарной ячейки. Если n - число атомов в элементарной ячейке, М - масса атома, а V -объем элементарной ячейки, то плотность .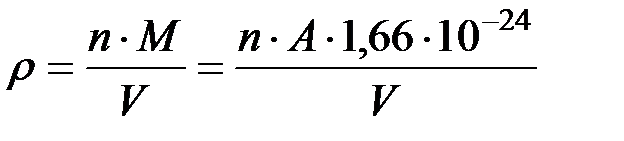

Масса одного атома металла М здесь подсчитана путем умножения его атомной массы А на 1/12 массы изотопа атома углерода С¹², т.е. на 1,66-l0^{-24 г}

Вариант 12

1. Влияние примесей и других структурных дефектов на удельное сопротивление металлов.причинами рассеяния электронных волн в металле являются не только тепловые колебания узлов решетки, но и статические дефекты структуры, которые также нарушают периодичность потенциального поля кристалла. Рассеяние на статических дефектах структуры не зависит от температуры. Поэтому по мере приближения температуры к абсолютному нулю сопротивление реальных металлов стремится к некоторому постоянному значению, называемому остаточным сопротивлением. Отсюда вытекает правило Маттиссена об аддитивности удельного сопротивления: ,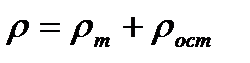

т.е. полное удельное сопротивление металла есть сумма удельного сопротивления, обусловленного рассеянием электронов на тепловых колебаниях узлов кристаллической решетки, и остаточного удельного сопротивления, обусловленного рассеянием электронов на статических дефектов структуры.

Исключение из этого правила составляют сверхпроводящие металлы, в которых сопротивление исчезает ниже некоторой критической температуры.

Различные примеси по-разному влияют на остаточное сопротивление металлических проводников. Эффективность примесного рассеяния определяется возмущающим потенциалом в решетке, значение которого тем выше, чем сильнее различаются валентности примесных атомов и металла – растворителя.

Помимо примесей некоторый вклад в остаточное сопротивление вносят собственные дефекты структуры — вакансии, атомы внедрения, дислокации, границы зерен. Концентрация точечных дефектов экспоненциально возрастает с температурой и может достигать высоких значений вблизи точки плавления. Кроме того, вакансии и междуузельные атомы легко возникают в материале при его облучении частицами высокой энергии, например, нейтронами из реактора или ионами из ускорителя. По измеренному значению сопротивления можно судить о степени радиационного повреждения решетки. Таким же образом можно проследить и за восстановлением (отжигом) облученного образца.

Большое влияние на удельное сопротивление металлов и сплавов оказывают искажения, вызываемые напряженным состоянием. Однако степень этого влияния определяется характером напряжений. Например, при всестороннем сжатии у большинства металлов удельное сопротивление уменьшается. Это объясняется сближением атомов и уменьшением амплитуды тепловых колебаний решетки.

Пластическая деформация и наклеп всегда повышают удельное сопротивление металлов и сплавов.

Термическая закалка приводит к повышению , что связано с искажениями решетки, появлением внутренних напряжений. При рекристаллизации путем термической обработки (отжига) удельное сопротивление может быть снижено до первоначального значения, поскольку происходит "залечивание" дефектов и снятие внутренних напряжений.

2. Определение плотности металлического образца. Оборудование: весы с укороченным коромыслом, набор разновесок, твердый образец произвольной формы, сосуды с дистиллированной водой и исследуемой жидкостью.

Расчет плотности исследуемого твердого образца ведется по формуле

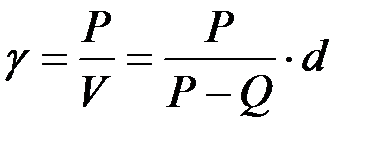
В качестве жидкости берут дистиллированную воду, плотность которой известна В системе “СИ” она равна d=1000 гр/м³.

Вес тела в воде Q и в воздухе Р можно измерить в граммах, т.к. отношение 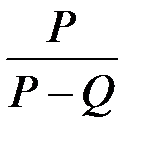- безразмерная величина и размерность измеряемой плотности образца

будет такая же, какова размерность d жидкости.

Для определения плотности твердого тела необходимо:

1. Взвесить исследуемый образец в воздухе (Р). Измерение произвести 2 раза. Перед каждым измерением проверять установку весов. Найти среднее значение Р.

2. Подвеситъ образец на тонкой проволочке к крючку левой чашки весов. Подставить под чашку весов сосуд с дистиллированной водой и погрузить в него тело. Следитъ, чтобы оно не касалось дна и стенок сосуда и было полностью погружено в воду. Определить 2 раза кажущийся вес тела в жидкости Q. Найти среднеарифметическое значение Q.

3. Зная d воды, по формуле

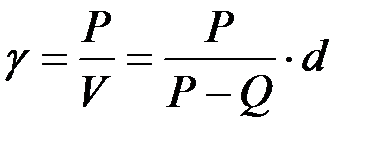
определить плотность исследуемого образца 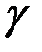по средним значениям Р и Q.

Вариант 13

1. Электрические свойства металлических сплавов.Статистическое распределение атомов разных сортов по узлам кристаллической решетки вызывает значительные флуктуации периодического потенциального поля кристалла, что в свою очередь, приводит к сильному рассеянию электронов. Как и в случае металлов, полное сопротивление сплава можно выразить в виде суммы двух слагаемых:

,

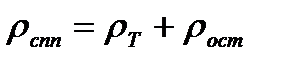где 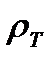– сопротивление, обусловленное рассеянием электронов на тепловых колебаниях решетки; 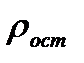— добавочное (остаточное) сопротивление, связанное с рассеянием электронов на неоднородностях структуры сплава.

Специфика твердых растворов состоит в том, что рост может существенно (во много раз) превышать тепловую составляющую.

Для многих двухкомпонентных сплавов изменение 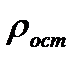в зависимости от состава хорошо описывается параболической зависимостью вида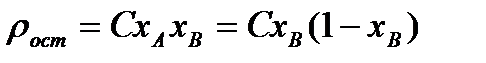

где С — константа, зависящая от природы сплава; х_А и х_в — атомные доли компонентов в сплаве. Закон Нордгейма.

Закон Нордгейма довольно точно описывает изменение удельного сопротивления непрерывных твердых растворов в том случае, если при изменении состава не наблюдается фазовых переходов и ни один из их компонентов не принадлежит к числу переходных или редкоземельных элементов. Примером подобных систем могут служить сплавы Au — Ag, Cu- Ag, Cu — Au, W — Мо

Несколько иначе ведут себя твердые растворы, компонентами которых являются металлы переходной группы (рисунок 4.10). В этом случае при высоких концентрациях компонентов наблюдается существенно большая величина остаточного сопротивления, что связано с переходом части валентных электронов на внутренние незаполненные d — оболочки атомов переходных металлов. Кроме того, в подобных сплавах максимальное 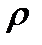часто соответствует концентрациям, отличным от 50%.

Чем больше удельное сопротивление сплава, тем меньше его 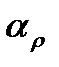. Это вытекает из того, что в твердых растворах рост, как правило, существенно превышает 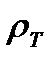и не зависит от температуры.

Во многих случаях температурная зависимость удельного сопротивления сплавов оказывается более сложной, чем та, которая вытекает из простой аддитивной закономерности. Температурный коэффициент удельного сопротивления сплавов может быть существенно меньше, чем предсказывает соотношение .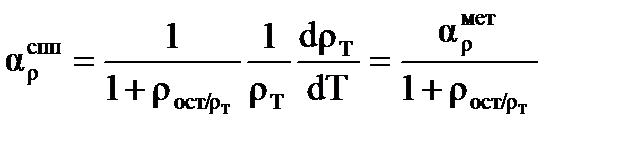

2. Определение плотности жидкости.Плотность жидкости можно найти пользуясь формулой (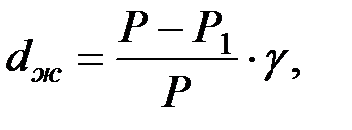

где d_ж – плотность исследуемой жидкости;

- плотность твёрдого образца;

Р – вес твёрдого образца в воздухе;

Р₁ – вес твёрдого образца в исследуемой жидкости.

Плотность жидкости определяют следующим образом:

1. Протереть поверхность твёрдого образца.

2. Образец подвесить на проволочке к крючку левой чашки весов и опустить в сосуд с исследуемой жидкостью. Следить, чтобы он не касался дна и стенок сосуда. Определить кажущийся вес образца в жидкости Р₁ (измерить 2 раза). Найти среднее значение Р₁.

3. Определить плотность исследуемой жидкости по средним величинам Р, Р₁ и . Численные значения Р и 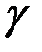взять из предыдущего эксперимента.

Вариант 14

1. Влияние толщины металлических пленок на удельное поверхностное сопротивление и его температурный коэффициент.При производстве интегральных схем металлические пленки используются для межэлементных соединений, контактных площадок, обкладок конденсаторов, индуктивных, магнитных и резистивных элементов.

Структура пленок в зависимости от условий конденсации может изменяться от аморфного конденсата до эпитаксиальных пленок – структур совершенного монокристаллического слоя. Кроме этого, свойства металлических пленок связаны с размерными эффектами. Так их вклад электропроводность существенен, если толщина пленки соизмерима с l_ср .

типичные зависимости поверхностного сопротивления тонких пленок р, и его температурного коэффициента 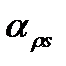от толщины пленки

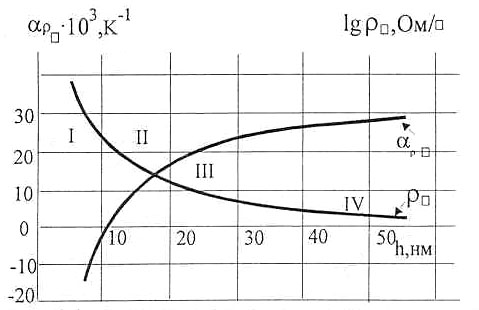
Характер изменения 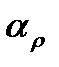_□ и 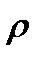_□ от толщины пленки h

I - образование и рост островков металла

II - касание островков между

III - образование проводящей сетки, когда уменьшаются размеры и число промежутков между островками;

IV - формирование сплошной проводящей пленки, когда проводимость и 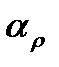_□ приближаются к значению массивных проводников, но все-таки удельное сопротивление пленки больше, чем у объемного образца, из-за высокой концентрации дефектов, примесей, захваченных в пленку при осаждении. Поэтому пленки, окисленные по границам зерен, являются электрически прерывными, хотя физически они сплошные. Вносит вклад в рост 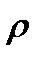_□ и размерный эффект из-за снижения длины свободного пробега электронов при отражении их от поверхности образца.

При изготовлении тонкопленочных резисторов применяется три группы материалов: металлы, сплавы металлов, керметы.

2. Определение зависимости удельного электрического сопротивления проводников и полупроводников от температуры.Среди электрических характеристик материалов наиболее важ­ное место занимает их удельное электрическое сопротивление.

Удельное электрическое сопротивление - отношение падения напряжения на единице длины определенного участка образца к плотности постоянного тока, протекающего через него.

В зависимости от величины удельного электрического сопро­тивления различают: 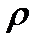. Ом ×м

проводники <10^-3…10^-5;

полупроводники 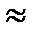10^-6…10⁷;

диэлектрики 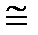l0⁷...10¹⁸.

Отичие проводников от полупроводников проявляется также в характере изменения величины их удельного электросопротивления при воздействии температурных полей. С повышением темпера­туры электросопротивление проводников увеличивается, полупроводников - уменьшается.

Удельное электрическое сопротивление образца вычисляют по формуле:

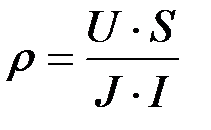,Ом∙м,

где U—падение напряжения на испытуемом участке образца, В

J — сила постоянного тока, протекающего через образец, А;

S — площадь поперечного сечения образца, м²;

е — длина участка образца, на котором измеряют падение на­пряжения, м.

Вариант 15

1. Явление теплового расширения.При нагреве металлов и сплавов наблюдается явление теплового расширения, являющееся следствием асимметрии сил притяжения и отталкивания, действующих между атомами, а также фазовых и структурных превращений, происходящих в некоторых из них.

Явление теплового расширения и связанное с ним изменение объема обратимо и если в образце при нагреве или охлаждении не происходят структурные или фазовые превращения, то при снижении (повышении) температуры к первоначальному уровню восстанавливаются и исходные размеры образца. Помимо обратимого изменения размеров образцы могут изменять свои размеры и необратимо вследствие фазовых и структурных превращений. При фазовых превращениях I рода, сопровождающихся изменением типа, симметрии или размеров кристаллической решетки, объем изменяется скачкообразно в соответствии с изменением ее компактности. При фазовых превращениях II рода изменения объема плавные - меняется характер их зависимости от температуры; знак и величина изменений зависят от характера этих превращений.

Измерение длины (или объема) во времени в изотермических условиях позволяет определить кинетику превращений поскольку степень развития этих превращений во времени пропорциональна изменениям длины Изменение размеров тел при нагреве и охлаждении, температурно-временные условия развития фазовых превращений и сопровождающие их объемные эффекты изучают с помощью дилатометрического анализа.

Достоинством дилатометрического анализа по сравнению с термическим является независимость его результатов от скорости охлаждения или нагрева (если при этом не изменяется тип превращения).

2. Электрические свойства.Закон Ома – основа изучения электрических свойства металлов и их сплавов. Основой изучения электрических свойств металлов и их сплавов является закон Ома, связывающий прямой пропорциональностью разность потенциалов на концах проводника Е и силу тока (i), по нему протекающего. Е и i связаны коэффициентом пропорциональности – сопротивлением проводника. Неоднократно проверялась правильность закона Ома. Проведенная проверка показала, что до очень большой плотности тока (10⁶ А/см²) в исследованных золоте, серебре, меди, платине и вольфраме не наблюдается отклонений от закона Ома. Только при еще более высоких плотностях тока в двух последних элементах, являющихся переходными, авторы наблюдали некоторое увеличение сопротивления.

Закон Ома положен в основу экспериментального изучения, электрических свойств металлов и их сплавов.

Константой, характеризующей электрические свойства металла, является его удельное сопротивление 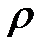. Оно определяется природой объекта и не зависит от его формы и размеров. Как известно, 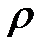может быть получено измерением сопротивления r на образце длиной l и сечением s; вычисляется 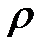из формулы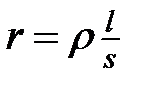

где r для металлических проводников, Ом; l – м; s – мм²;

В этом случае 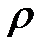будет выражено в Ом·мм²/м.

Другими, также часто встречающимися обозначениями тех же величин являются мкОм, см и см²; в этом случае 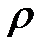измеряется в мкОм·см. Нетрудно подсчитать, что числовые значения 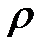при первом обозначении будут в 100 раз меньше, чем при втором. Например, для технически чистого железа 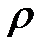= 0,10 Ом·мм²/м, или 10мкОм·см. Другими словами, сопротивление 1 см³ железа равняется 10 мкОм (условное обозначение 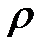в мкОм/см³).

Удельная проводимость 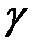является величиной, обратной удельному сопротивлению, и вычисляется из уравнения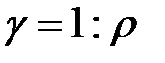

В соответствии с этим 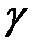измеряется в м/Ом·мм², или мкОм^-1·см^-1, или Ом^-1·см^-1.

Вариант 16

1. Определение критических точек металлов и сплавов методом термического анализа.Известно, что любое изменение состояния металлов и сплавов (фазовое, внутрифазовое или структурные превращения) вызывает изменение энтальпии, а потому должно сопровождаться тепловым эффектом - выделением или поглощением тепла. Таким образом, если при нагреве или охлаждении удается зафиксировать тепловой эффект, о котором можно судить и по изменению температуры металла, то можно выявить вид превращения и определить условия, способствующие или тормозящие превращение. В практике металловедения наибольшее применение получил термический анализ, экспериментальная техника проведения которого является менее сложной. В случае термического анализа изменение энтальпии характеризуется изменением температуры, обычно фиксируемой в функции времени нагрева или охлаждения металла.

При термическом анализе автоматически записывается или строится по экспериментальным данным графическая зависимость - изменение температуры во времени в процессе нагрева (или охлаждения) с постоянной скоростью. Появление теплового эффекта вызывает при соответствующей температуре появление различного вида аномалии (ступеней, перегибов), поэтому он может быть зарегистрирован, а тем самым выявлено соответствующее превращение. Использование различных схем термического анализа в сочетании с высокочувствительной измерительной аппаратурой позволяет достаточно надежно определять температуры превращений при изменении агрегатного состояния (например, при плавлении или затвердевании), при полиморфном превращении, эвтектоидном и других превращениях.

2. Теории теплопроводности Дебая.В 1912г. Питер Дебай (1884-1966) косвенным путем показал, что квантовая теория позволяет объяснить аномальные результаты измерений удельной теплоемкости. Теория Дебая правильно предсказывала зависимость удельной теплоемкости от температуры, а ширину участка этой зависимости в шкале температур можно было приписать величине силы взаимодействия атомов твердого тела. В квантовой теории теплоемкости Дебая кристалл, состоящий из N упруго связанных друг с другом атомов (ионов), рассматривается как связанная система, которая обладает 3N степенями свободы. Такая система обладает спектром частот колебания. Закон теплоемкости Дебая используют для оценочных расчетов теплоемкости, теплопроводности, электропроводности веществ, рассеяния излучений веществами при низких температурах порядка 0 - 100 К. Для проведения таких расчетов для каждого вещества подобрана по сопоставлению с экспериментальными данными своя температура Дебая. Закон теплоемкости Дебая используют для технических расчетов в криогенной технике (устройств для хранения и транспортировки сжиженных газов, устройств для охлаждения до низких температур). Из закона Дебая следует, что при низких температурах теплоемкость мала, поэтому малые количества тепла, сообщенные системе, приводят к большим изменениям температуры входящих в систему тел. Из-за этого в системе возникают большие температурные напряжения, которые надо учитывать при проектировании технических систем.

Вариант 17

1. Теории теплопроводности Эйнштейна.В 1907г. Альберт Эйнштейн (1879-1955) применил идею квантов к теории теплоемкости. В квантовой теории теплоемкости Эйнштейна каждый атом (ион), находящийся в узле кристаллической решетки, рассматривается как квантованный осциллятор. Все осцилляторы колеблются с одинаковой частотой w. Предположение о том, что атомы колеблются независимо, неверно. Теория Эйнштейна.
Из решения уравнения Шредингера для гармонического осциллятора следует, что он может находиться лишь в дискретных энергетических состояниях, разделенных энергией hw . Это значит, что он может поглощать энергию только малыми порциями, равными hw, и любой колеблющийся осциллятор( например маятник) может “выбирать” значения амплитуды своего колебания лишь из определенного набора разрешенных амплитуд.
Теория Эйнштейна дает лишь качественно правильный ход теплоемкости при низких температурах. Количественного согласия с опытом удалось достигнуть Дебаю.

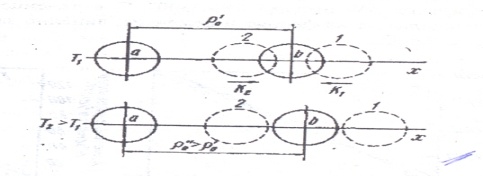
2. Плотность и термическое расширение. Плотностью металла d называется масса единицы объема этого металла. Зная массу m и объем V металла, можно вычис­лить d: d = m/V. Удельный объем V металла характеризует объем единицы массы этого металла и является, следовательно, величиной, обратной плотности: V = l/d.

Определение плотности металла сводится к определению массы и объема испытуемого образца. Масса измеряется при помощи аналитических весов. Что касается определения объема, то его можно производить двумя методами: пикнометрически и гидростатически. Пикнометрический метод сводится к определению объема вытесненной жидкости при по­гружении в нее испытуемого металлического образца. Точность нахождения объема этим методом определяется ценой деления используемой мензурки и четкостью края мениска жидкости в ней. В качестве жидкости, в которую погружается образец, следует выбирать бензол, спирт и тому подобные вещества, обладающие хорошей смачивающей способностью.

Модель из двух атомов, иллюстрирующая тепловое расширение:

Вариант 18

1. Теплопроводность металлов и сплавов.Теплопроводностью называется явление передачи энергии от более нагретых участков тела к менее нагретым в результате теплового движения и взаимодействия частиц, из которых состоит тело.

Наибольшей теплопроводностью обладают металлы — она у них в сотни раз больше, чем у воды.

В массивную латунную шайбу вкручено пять стержней: стальной, латунный, алюминиевый, медный и железный. На каждом из стержней закреплены воском три спички. Греем шайбу на пламени спиртовки или свечи – через несколько секунд падает первая спичка: ближняя к шайбе на медном стержне. Тепло быстро распространилось по медному стержню и расплавило восковую подошву ближней к шайбе спички. Следующей будет спичка на алюминиевом стержне, потом – на латунном, железном… К этому моменту с медного и алюминиевого стержней упадет уже по нескольку спичек. Последней падает крайняя спичка на стальном стержне.

Чем меньше теплопроводность металла, тем больше опасность образования трещин при нагреве. Например, теплопроводность сталей, особенно легированных, в пять раз меньше теплопроводности меди и алюминия. С теплоемкостью связан расход топлива для нагрева заготовки до нужной температуры.

l 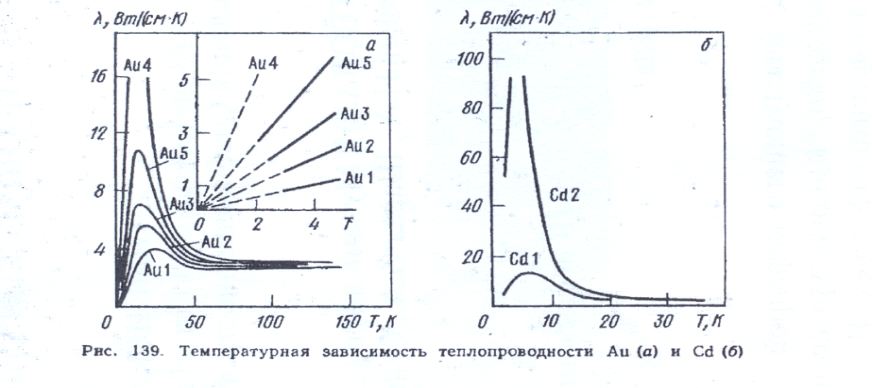Au1-неотожжен -99,9%

l Au2- отожжен в вакууме при 700⁰ С в течении 3ч.

l Au3- 99,999% -волочением прутка диаметром 3мм.

l Au4- отожжен в вакууме при 700⁰ С в течении 3ч.

l Au5- отожжен в вакууме при 700⁰ С в течении 3ч.+волочение

Теплопроводность углеродистой стали после закалки1,14 % С, 0,12% Si, и 0,20%Mn b1-780, b2-840, b3-900, b4- 1000⁰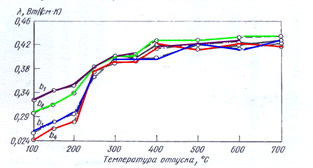

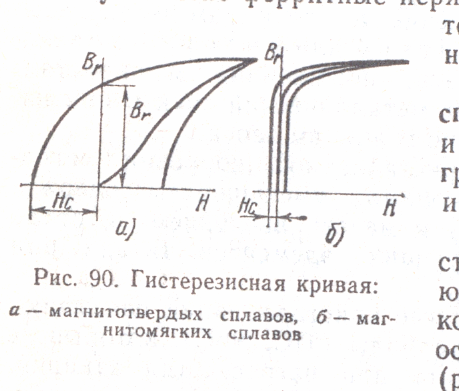
2. Магнитотвердые магнитные материалы.Магнитотвердые материалы, напротив, имеют большую коэрцитивную силу, высокие значения объемной плотности энергии, малую магнитную проницаемость. К магнитотвердым материалам относятся стали с высоким содержанием углерода (ЕХ3, ЕВ6, ЕХ5К5), алнико - сплавы железа с алюминием, никелем, кобальтом, магнитотвердые ферриты, викаллой сплав железа с ванадием, соединения на основе редкоземельных элементов -самария, празеодима и др.

Вариант 19

1. Виды проводников.Проводники электрического тока могут быть твердыми телами, жидкостями, а при выполнении ряда условий и газами.

Твердые проводники – металлы и некоторые модификации углерода. По величине удельного сопротивления металлические проводники делятся на следующие группы:

- сверхпроводники;

- криопроводники;

- металлы и сплавы с высокой удельной проводимостью ;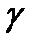

- металлы и сплавы со средним значением ;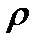

- металлы и сплавы с высоким значением .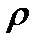

За исключением Сu, Аg, Аu, Рt, щелочных, щелочноземельных и ферромагнитных металлов большая часть остальных металлов является сверхпроводниками [1]. К сверхпроводникам относятся интерметаллические соединения Nb₃Х или V₃Х, где Х – переходный материал; тройные сверхпроводники (фазы Шевреля RМО₆Z₈, где R – катион, Z – атом халькогена). Существуют экзотические сверхпроводники: сверхпроводники с тяжелыми фермионами, например:

- СеСu₂Si₂ (Тс – 0,5К) открыт в 1979г.;

- с низкой электронной концентрацией: Ва(Вi_1-х Рb_х)О₃ при 13К;

- неорганические сверхпроводники с низкой размерностью: трихалькогениды ниобия и тантала (NbSе₃, ТаSе₃);

- органические сверхпроводники: соли тетрацианохинодиметана (ТСNО), соли Бехгорда (ТМТSF)₂Х, где Х = РF₆, СlО₄, RеО₄, FSО₃.

- невоспроизводимые сверхпроводники: СuСl, СdS, NbSi.

Особую группу составляют высокотемпературные сверхпроводники с точками перехода 17К – 105К – 133К; Ybа₂Сu₃О_7±δ; Вi₂Sr_3-хСd_хСu₂О_g-δ; Ва_0,2Lа_1,8СuО₄; Ybа₂Сu₃О_6±х; Lа_2-хSr_хСuО₄; Ва₂Sr₂СаСuО₄ и др.

Подробнее с механизмами высокотемпературной сверхпроводимости можно познакомиться в.

Криопроводники имеют 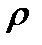на два порядка выше, чем сверхпроводники, при более высоких температурах, чем сверхпроводимость. Например, при температуре жидкого азота Аl, Ве – криопроводники.

Представители материалов с высоким удельным сопротивлением 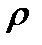и высокой удельной проводимостью 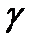, их области применения далее рассмотрим отдельно

2. Дефекты решетки.. Различают по геометрическим признакам: точечные, линейные, поверхностные.

Точечные дефекты:

- вакансии (дефекты Шоттки),

- межузельные атомы (дефекты Френкеля).

Вакансии возникают при переходе атомов из узла решетки на поверхность или из-за испарения и реже в результате перехода в междоузлие.

Тепловые вакансии характерны для поверхностного расположения атомов. С ростом температуры концентрация вакансий растет.

При достижении температуры плавления Т такие вакансии достигнут 1% по отношению к числу атомов в кристалле. Быстрым охлаждением можно зафиксировать такие закалочные вакансии. Вакансии могут быть двойные, тройные. Наличие вакансий определяет диффузию. Дефекты Шоттки и Френкеля влияют на проводимость, магнитные и другие свойства металлов.

Линейные дефекты

Чаще всего краевые и винтовые дислокации. Вокруг дислокации на протяжении нескольких межатомных расстояний возникают искажения решетки. Вектор Бюргера — критерий такого искажения – разность периметров контуров вокруг данного атома в плоскости удельной решетки и вокруг центра дислокации в реальной решетке.

Поверхностные дефекты

Эти дефекты малы только в одном измерении и представляют собой поверхности раздела между отдельными зернами.

Зерно 1 Пограничный слой Зерно 2

3 - 4 межатомных расстояний

Вариант 20

1. Твердые растворы с неограниченной растворимостью.Твердые растворы с неограниченной растворимостью образуются при условиях:

— одинаковые типы кристаллических решеток у А и В;

— различие в атомных размерах ≤8 — 15%;

— близкое строение валентной оболочки электронов в атоме. Например, Au + Ag с ГЦК решеткой или Мо + W.

2. Виды проводников.Проводники электрического тока могут быть твердыми телами, жидкостями, а при выполнении ряда условий и газами.

Твердые проводники – металлы и некоторые модификации углерода. По величине удельного сопротивления 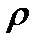металлические проводники делятся на следующие группы:

- сверхпроводники;

- криопроводники;

- металлы и сплавы с высокой удельной проводимостью ;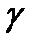

- металлы и сплавы со средним значение ;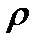

- металлы и сплавы с высоким значением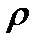

За исключением Сu, Аg, Аu, Рt, щелочных, щелочноземельных и ферромагнитных металлов большая часть остальных металлов является сверхпроводниками . К сверхпроводникам относятся интерметаллические соединения Nb₃Х или V₃Х, где Х – переходный материал; тройные сверхпроводники (фазы Шевреля RМО₆Z₈, где R – катион, Z – атом халькогена). Существуют экзотические сверхпроводники: сверхпроводники с тяжелыми фермионами, например:

- СеСu₂Si₂ (Тс – 0,5К) открыт в 1979г.;

- с низкой электронной концентрацией: Ва(Вi_1-х Рb_х)О₃ при 13К;

- неорганические сверхпроводники с низкой размерностью: трихалькогениды ниобия и тантала (NbSе₃, ТаSе₃);

- органические сверхпроводники: соли тетрацианохинодиметана (ТСNО), соли Бехгорда (ТМТSF)₂Х, где Х = РF₆, СlО₄, RеО₄, FSО₃.

- невоспроизводимые сверхпроводники: СuСl, СdS, NbSi.

Особую группу составляют высокотемпературные сверхпроводники с точками перехода 17К – 105К – 133К;

Криопроводники имеют 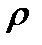на два порядка выше, чем сверхпроводники, при более высоких температурах, чем сверхпроводимость.