Зависимость полной энергии двух атомов кислорода от расстояния между ними
Полную энергию Etot многоэлектронных систем, в общем виде можно представить в виде следующих слагаемых:
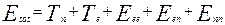 (2.12)
(2.12)
Где Tn – кинетическая энергия ядер, соответствующий оператор записывается как:
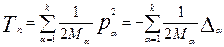
Te- кинетическая энергия электронов,
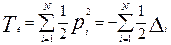
Eee – энергия взаимодействия электронов между собой. Потенциал взаимодействия электронов при кулоновском взаимодействии:
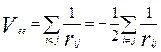
rij – расстояние между электронами с индексами i и j.
Een – энергия взаимодействия электронов с ядрами.
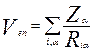
Где Zα – заряд ядра α, Riα – расстояние между электроном i и ядром α.
Enn- энергия взаимодействия ядер между собой. Потенциал записывается в следующем виде:
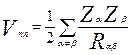
Rαβ – расстояние между ядрами с индексами α и β.
Масса ядер как минимум на три порядка превышает массу электронов, поэтому, в приближении Борна-Оппенгеймера, кинетической энергией ядер пренебрегают, ввиду ее малости.
Рассмотрим процесс последовательного сближения двух атомов кислорода с бесконечности. Обычно кривая потенциальной энергии имеет аттрактивный характер (притяжение) на больших расстояниях, при достижении определенного рас r0 стояния начинает преобладать отталкивание. Значение r0 – равновесное расстояние между атомами в основном состоянии образовавшейся молекулы.
Проведем ряд расчетов полной энергии системы, состоящей из двух атомов кислорода, в зависимости от расстояния между ними от 0.6 Å до 2 Å с шагом 0.1 Å. Метод DFT B3LYP 6-31(d)G, Spin - триплет. Для просмотра рассчитанного значения полной энергии открываем (File → Open) выходной файл, например, O_DFT_B3LYP_6-31dG_trip_energy.log, затем на панели команд редактора GaussView выбираем Results → Summary. Появляется окно Gaussian Calculation Summary (рис.2.5). В поле E(метод расчета) приведено значение полной энергии молекулы в атомных единицах энергии 1a.u.=1Хартри=27.2 эВ.
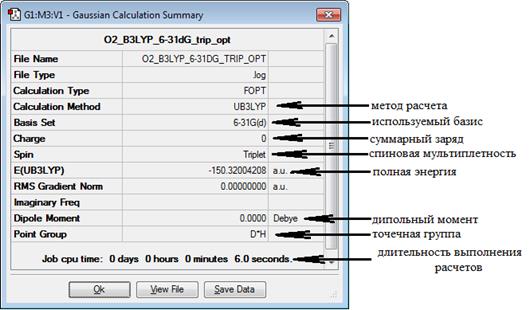
Рис.2.5 Основные результаты расчетов, представленные в Gaussian Calculation Summary
Зависимость полной энергии двух атомов кислорода от расстояния r между ними представлена на рис.2.6. Минимуму энергии соответствует r=r0≈1.2 Å.
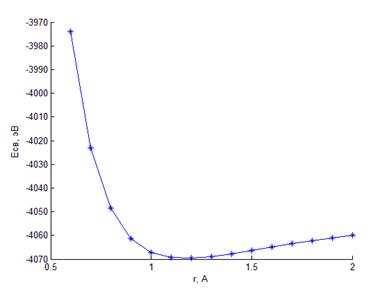
Рис. 2.6 Зависимость полной энергии двух атомов кислорода от расстояния между ними
Задание 2. Построить и сравнить зависимости полной энергии двух атомов кислорода от расстояния между ними при двух значениях мультиплетности: синглет и триплет методом DFT B3LYP 6-31(d)G. По минимуму значения полной энергии выделить значения r, при которых энергетически выгоднее синглетное или триплетное состояние.
Изменение расстояния между атомами изменяет не только полную энергию, но и оказывает существенное влияние на перераспределение электронной плотности. На рис.2.7 представлен процесс перестройки орбиталей атомов кислорода при изменении расстояния между ними.
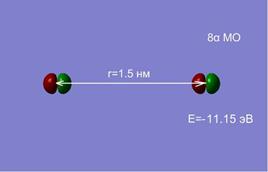 а а | 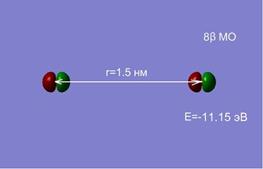 б б |
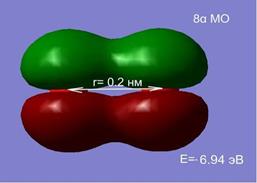 в в | 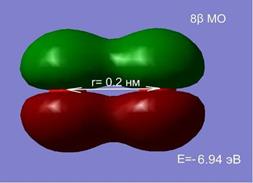 г г |
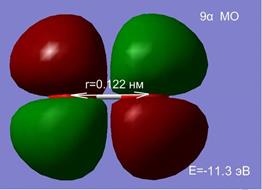 д д | 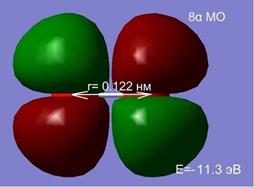 е е |
Рис. 2.7 Влияние межатомного расстояния на энергию и электронную плотность МО при сближении двух атомов кислорода.
На расстоянии 1.5 нм состояния являются вырожденными, а внешняя МО системы из двух атомов, соответствует двум 2p-АО (рис. 2.7. а, б). Сближение атомов приводит к перераспределению электронной плотности и изменению энергий МО. При r=0.2 нм наблюдается деформация 8 МО и образование метастабильного состояние молекулы О2 в синглетном состоянии (в, г). При дальнейшем сближении атомов синглетное состояние становится энергетически не выгодным, и молекула переходит в основное триплетное состояние при равновесном расстоянии r0≈ 1.2 Å.
Это интересно: Триплетность, а, следовательно, и спиновая нескомпенсированность (разное число электронов с направлением спина электронов «вверх» и «вниз»), основного состояния молекулы O2 означает, что молекула обладает спиновым магнитным моментом. Действительно, жидкий кислород притягивается к полюсам магнита точно так же, как притягиваются железные опилки. Жидкий кислород – одна из немногих жидкостей с такими удивительными свойствами.
