Применение первого закона термодинамики
Основные понятия и определения химической термодинамики
Химическая термодинамика имеет дело с термодинамическими системами. Термодинамической системой называется тело или группа тел, находящихся во взаимодействии друг с другом и которые мысленно обособлены от окружающей среды. Различают изолированные и не изолированные системы. Система, которая не обменивается с окружающей средой теплотой и работой называется изолированной. Энергия и объём такой системы постоянны.
Если система обменивается с окружающей средой веществом и энергией, то она называется открытой. Если система обменивается с окружающей средой только энергией, то она называется закрытой. Системы, в которых это условие не соблюдается, называются неизолированными.
Различают также гомогенные и гетерогенные системы. Система называются гомогенной, если она состоит из одной фазы. Если система состоит из двух и более фаз, то она называется гетерогенной. Фазой называется гомогенная часть системы, характеризующаяся одинаковыми физико-химическими свойствами и отделенная от других частей системы поверхностью раздела.
Термодинамическая система характеризуется различными физико – химическими свойствами, которые называются термодинамическими параметрами или просто параметрами. Так идеальный газ характеризуется такими параметрами как температура Т, объём V и давление Р. Все параметры системы связаны между собой. Эту связь выражает уравнение состояния системы. Если система характеризуется такими параметрами как Т, V и P, то в общем виде уравнение состояния системы выражается уравнением
(Т,V,P) = 0 (1.1)
В качестве примера конкретного уравнения состояния может служить уравнение состояния идеального газа (уравнение Менделеева-Клапейрона)
РV = nRT, (1.2)
где n - число молей идеального газа,
R = 8,314 - универсальная газовая постоянная, 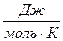 .
.
Состояние системы считается однозначно определённым, если известны все её свойства. Для определения состояния системы необязательно измерять все из них. Достаточно определить несколько свойств. Другие могут быть рассчитаны из уравнения состояния системы. Так для определения состояния идеального газа достаточно измерить два каких-либо свойства. Величина третьего свойства будет иметь строго определённое значение согласно уравнению состояния. Таким образом, для определения состояния идеального газа достаточно знать два любых свойства. Минимальное число параметров, которое необходимо знать для определения состояния системы, называются независимыми параметрами или независимыми переменными.
Свойства системы можно разбить на две группы: экстенсивные и интенсивные. Экстенсивными называются свойства, которые зависят от массы системы. Примером экстенсивного свойства может служить объём системы. Интенсивными называются свойства, которые не зависят от массы системы. Примером таких свойств идеального газа могут служить температура и давление.
В термодинамической системе протекают термодинамические процессы. Термодинамическим процессом называется всякое изменение в системе, связанное с изменением хотя бы одного параметра. Различают следующие основные термодинамические процессы, протекающие в системе:
- процесс, протекающий при постоянной температуре (Т = const), который называется изотермическим;
- процесс, протекающий при постоянном объёме (V=const)- изохорный;
- процесс, протекающий при постоянном давлении (P=const) – изобарный;
- процесс, протекающий при постоянных температуре и объёме (T = const и V = cоnst), – изохорно- изотермический;
- процесс, протекающий при постоянных температуре и давлении (Т =const и P = const), - изобарно – изотермический.
Процесс, при котором термодинамическая система, выйдя из некоторого начального состояния и претерпев ряд изменений, возвращается в то же самое состояние, называется круговым процессом или циклом. При протекании кругового процесса изменение любого параметра системы равно нулю.
Изменение некоторых свойств системы не зависит от пути протекания процесса, а зависит только от начального и конечного состояния системы. Такое свойство системы называются функцией состояния. К таким функциям можно отнести термодинамические параметры системы Т, Р и V. Любая функция состояния характеризуется полным дифференциалом.
Конечным состоянием протекания любого процесса в термодинамической системе является состояние равновесия. Состоянием равновесия называется такое состояние, при котором параметры системы остаются неизменными во времени без каких-либо изменений в окружающей среде. Если параметры системы остаются постоянными во времени за счёт каких – либо изменений в окружающей среде, то такое состояние называется стационарным.
1.2 Внутренняя энергия, теплота и работа.
Первый закон термодинамики
Внутренней энергией называется сумма кинетической энергии движения частей системы и потенциальной энергии их взаимодействия между собой. Абсолютную величину внутренней энергии системы ни определить, ни рассчитать невозможно. Химическая термодинамика позволяет определять и рассчитывать изменение внутренней энергии системы при переходе системы из одного состояния в другое. Все изменения внутренней энергии при переходе системы из одного состояния в другое можно разделить на две группы: изменения энергии, связанные с передачей теплоты и изменения энергии, связанные с совершением работы. Таким образом, теплота и работа являются формами перехода внутренней энергии от одного тела к другому. Они измеряются в тех же единицах, что и энергия. Взаимосвязь между внутренней энергией, теплом и работой устанавливает первый закон термодинамики, который гласит: теплота, подведённая к системе, расходуется на изменение внутренней энергии и совершение работы:
Q = ΔU + A, (1.3)
где Q – теплота, Дж
ΔU – изменение внутренней энергии, Дж
А – работа, Дж.
Изменение внутренней энергии не зависит от пути протекания процесса, а определяется лишь начальным и конечным состоянием системы. Это значит, внутренняя энергия является функцией состояния системы. Теплота и работа в общем случае не являются функциями состояния системы и их изменение зависит от пути процесса. С учётом этого математическая формулировка первого закона термодинамики будет иметь вид:
δQ = dU + δA, (1.4)
где dU – полный дифференциал внутренней энергии системы;
δQ – бесконечно малое изменение теплоты;
δА – бесконечно малое изменение работы.
В последнем уравнении знак полного дифференциала (d) характеризует функцию состояния системы U, а знак δ характеризует бесконечно малое изменение свойств системы Q и А, которые не являются функциями состояния.
Для изолированных систем справедливо, когда δQ = 0 и δA = 0, уравнения (1.3) и (1.4) примут вид:
dU = 0 или ΔU = 0 (1.5)
Из уравнения (1.5) следует, что внутренняя энергия изолированных систем постоянна:
U = Const (1.6)
Уравнение (1.6) представляет собой математическую формулировку первого закона термодинамики для изолированных систем.
Изменение внутренней энергии системы может происходить за счёт обмена теплотой и работой с окружающей средой. В химической термодинамике принято называть теплоту положительной (Q > 0), если система поглощает теплоту, и отрицательной (Q < 0), если система выделяет теплоту в окружающую среду. Работу принято считать положительной (A>0), если система совершает работу над окружающей средой, и отрицательной (A<0), если окружающая среда совершает работу над системой. Если системой является идеальный газ, то положительной работой является работа расширения, а отрицательной – работа сжатия.
Первый закон термодинамики является постулатом, выведенным из многовекового опыта человеческой деятельности. Все формулировки первого закона равноценны. Если принять одну из них за основу, то другие получаются из неё как следствия.
Применение первого закона термодинамики
К идеальным газам
Если в качестве термодинамической системы выбран идеальный газ, то единственной работой в уравнении первого закона термодинамики является работа расширения (сжатия) идеального газа, которая вырaжается уравнением:
δA = PdV (1.7)
С учётом работы расширения идеального газа уравнение первого закона термодинамики можно записать в виде:
δQ = dU + PdV (1.8)
Рассмотрим применение первого закона термодинамики к различным процессам.
1.3.1 Изотермический процесс
Внутренняя энергия идеального газа не зависит от давления и объёма газа, а зависит только от температуры. Если температура системы постоянна, то и внутренняя энергия системы будет оставаться постоянной ( U = const) или
dU = 0 (1.9)
Тогда уравнение первого закона термодинамики для изотермического процесса можно записать в виде:
δQ = PdV (1.10)
Интегрирование уравнения в пределах 1 – 2 состояния системы даёт:
QТ = 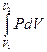 (1.11)
(1.11)
С учётом уравнения состояния идеального газа (1.2) получим:
QТ = 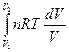 (1.12)
(1.12)
Откуда получим:
QT = nRTln 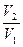 (1.13)
(1.13)
Для изотермического процесса справедливо соотношениe:
P1V1 = P2V2 (1.14)
Тогда для изотермического процесса можно записать:
QT = nRTln 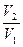 = nRTln
= nRTln 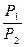 (1.15)
(1.15)
1.3.2 Изохорный процесс
Для изохорного процесса (V = const), при котором работа не совершается (δA = 0), уравнение первого закона термодинамики принимает вид:
δQV = dU (1.16)
Изменение внутренней энергии при протекании изохорного процесса определяется уравнением:
dU = nCVdT (1.17)
или в интегральной форме
QV = ΔU = nCV(T2-T1), (1.18)
где СV – теплоёмкость при постоянном давлении, 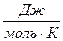 .
.
1.3.3 Изобарный процесс
Для изобарного процесса изменение внутренней энергии определится уравнением(1.18). Поскольку изобарный процесс протекает при постоянном давлении, то работа системы может быть определена по уравнению:
A = 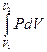 = P(V2 - V1) (1.19)
= P(V2 - V1) (1.19)
C учётом того, что PV1= nRT1 и PV2 = nRT2 , уравнение (1.19) примет вид:
A = nR(Т2 - Т1) (1.20)
Теплота, сопровождающая изобарный процесс, определяется из уравнения:
QP = nCP(T2 – T1), (1.21)
где СР - теплоёмкость при постоянном давлении, 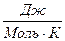 .
.
