Тепловой эффект химической реакции. Термохимия. Закон Гесса

Все химические процессы сопровождаются тепловыми эффектами.

Тепловым эффектом химической реакции называется теплота, выделяемая или поглощаемая в результате превращения исходных веществ в количествах, соответствующих уравнению химической реакции. При этом единственной работой является работа расширения, а исходные вещества и продукты реакции должны иметь одинаковую температуру.

Независимость теплоты химической реакции от пути процесса при р = const и Т = const (A = pDV) впервые была установлена в 1836 г. русским ученым Г.И. Гессом. Эта закономерность известна как закон Гесса: тепловой эффект химической реакции не зависит от пути ее протекания, а зависит лишь от природы и физического состояния исходных веществ и продуктов реакции.

Закон составляет теоретическую основу термохимии, т.е. раздела химической термодинамики, в котором вычисляются тепловые эффекты различных физико-химических процессов: химических реакций, фазовых переходов, процессов растворения и кристаллизации и т. д.

Следует помнить, что все термохимические расчеты проводятся при стандартных условиях: Т = 298 К (25 ⁰С), р = 101,3 кПа (1 атм.), например: DН⁰₂₉₈ – стандартная энтальпия.

В термохимии уравнение химической реакции записывается с указанием теплового эффекта реакции (энтальпии) и агрегатного состояния веществ. Эти уравнения называют термохимическими уравнениями:

Н_2(г) + Cl_2(г) = 2HCl_(г) DН⁰₂₉₈ = - 184,6 кДж.

В термодинамике принято:

- в экзотермических процессах теплота выделяется, для них DН < 0 и DU < 0 (теплосодержание и внутренняя энергия системы уменьшаются);

- в эндотермических процессах теплота поглощается, для них DН > 0 и DU > 0 (теплосодержание и внутренняя энергия системы возрастают).

В термохимических расчетах широко используются три следствия из закона Гесса.

Первое следствие: тепловой эффект прямой реакции равен тепловому эффекту обратной реакции с противоположным знаком: DН_пр.= - DН_обр.

Второе следствие: тепловой эффект реакции равен разности между суммой теплот (энтальпий) сгорания исходных веществ и суммой теплот (энтальпий) сгорания продуктов реакции с учетом стехиометрических коэффициентов веществ, участвующих в процессе:

DН_р.= S(n_i ^. DН_{сг i})_исх. - S(n_i ^. DН_{сг i} )_прод.,

где n_i – стехиометрический коэффициент для i-того вещества в уравнении реакции, ∆Н_{сг i} – теплота (энтальпия) сгорания i-того вещества.

Теплота (энтальпия) сгорания – количество теплоты, которое выделяется при полном сгорании одного моля вещества до высших окислов при данных условиях (р, Т). Численные значения теплот сгорания определяются по справочным изданиям.

Третье следствие: тепловой эффект реакции равен разности между суммой теплот (энтальпий) образования продуктов реакции и суммой теплот (энтальпий) образования исходных веществ с учетом стехиометрических коэффициентов веществ, участвующих в процессе:

DН_р.= S(n_i ^. DН_{обр. i})_прод. - S(n_i ^. DН_{обр. i} )_исх.,

где n_i – стехиометрический коэффициент для i-того вещества в уравнении реакции, ∆Н_{обр. i} – теплота (энтальпия) образования i-того вещества.

Под теплотой (энтальпией) образования понимается тепловой эффект реакции образования 1 моль вещества из простых веществ (измеряется в кДж/моль). Обычно используют стандартные энтальпии образования; их обозначают DН⁰_обр,298 или DН⁰_f,298 (часто один из индексов опускают и обозначают, например, DН⁰₂₉₈). Стандартные энтальпии простых веществ, устойчивых в стандартных условиях (газообразный кислород, жидкий бром, кристаллический йод, ромбическая сера, графит и т.д.) принимаются равными нулю. Численные значения теплот (энтальпий) образования определяются по справочникам.

Энтропия

Если на систему оказать внешнее воздействие, в системе происходят определенные изменения. Если после снятия этого воздействия система может вернуться в первоначальное состояние, то процесс является обратимым. Если после снятия внешнего воздействия систему и окружающую среду нельзя вернуть в первоначальное состояние, то процесс – необратимый.

Процессы, протекающие без подвода энергии от внешнего источника, называются самопроизвольными. Например: падение камня с высоты, переход тепла от более нагретого тела к менее нагретому, стекание воды по желобу. При этом система из более упорядоченного состояния переходит в состояние менее упорядоченное и более вероятное. Человеческий опыт показал, что самопроизвольные процессы в обратном направлении не могут протекать самопроизвольно, т.е. самопроизвольно камень не полетит вверх, теплота не перейдет от холодного тела к нагретому, а вода не потечет вверх по желобу.

Многие химические процессы также протекают самопроизвольно, например, образование ржавчины на железе, растворение соли в воде и др. Каковы движущие силы и критерии самопроизвольных процессов?

Частицам (молекулам, атомам, ионам) присуще стремление к беспорядочному движению, поэтому система стремится перейти из более упорядоченного состояния в менее упорядоченное. Так, если, например, баллон с газом (состояние I) соединить с сосудом, то газ из баллона будет распределяться по всему объему сосуда (состояние II). При этом система из более упорядоченного состояния (с меньшим беспорядком) переходит в состояние менее упорядоченное (с большим беспорядком). Количественной мерой беспорядка системы является термодинамическая функция состояния - энтропия (S). Ее численное значение можно определить следующим образом:

S = R ^. T ^. lnW, (10)

т.е. S пропорциональна lnW, где W – термодинамическая вероятность состояния системы или число вероятных микросостояний, которыми может быть реализовано данное макросостояние; W > 1.

При переходе системы из более упорядоченного состояния в менее упорядоченное (из состояния I в состояние II) энтропия системы возрастает, т.е. DS = S₂ – S₁ > 0.

Переход из менее упорядоченного состояния в более упорядоченное ( из состояния II в состояние I) без воздействия извне невозможен. Такой процесс называется несамопроизвольным. Понятно, что в рассматриваемом примере представляется невероятным, чтобы газ сам собой собрался в баллоне. Очевидно, что в этом случае энтропия системы уменьшается (DS = S₂ – S₁ < 0). Т.е.:

- все процессы, протекающие с уменьшением порядка в расположении частиц, сопровождаются увеличением энтропии, являются самопроизвольными процессами (процессы растворения, плавления, испарения, нагревания);

- все процессы, протекающие с увеличением порядка в расположении частиц, сопровождаются уменьшением энтропии, являются несамопроизвольными процессами (процессы конденсации, кристаллизации, охлаждения).

Таким образом, в изолированной системе самопроизвольные процессы протекают в сторону увеличения энтропии, DS > 0 (II закон термодинамики).

Системы, в которых протекают химические реакции, не являются изолированными, т.к. они сопровождаются тепловым эффектом, т.е. системы обмениваются энергией с окружающей средой. В неизолированных системах возможны процессы, в которых энтропия понижается. Например, при отводе тепла в окружающую среду расплав или стекло могут закристаллизоваться, а пар сконденсироваться (т.е. DS < 0).

В отличие от энтальпии, для любого вещества абсолютное значение энтропии можно вычислить либо определить экспериментальным путем. Энтропии веществ принято относить к стандартным условиям: Т = 298 К; Р = 101,3 КПа. Обозначают S⁰₂₉₈ и называют стандартной энтропией (численное значение стандартной энтропии определяется по справочным изданиям). Энтропия вещества измеряется в Дж/моль^.К.

Значениями энтропии веществ пользуются для определения изменения энтропии системы в результате соответствующих реакций. Например для реакции, записанной в общем виде:

аА +вВ + … = dD + eE + …

изменение энтропии выразится:

DS = (dS_D +eS_E + …) – (aS_A + bS_B + …) = S(n_i ·S_i)_прод. - S(n_i · S_i)_исх. (11)

Энтропия системы измеряется в Дж/К.

Свободная энергия Гиббса

Все химические реакции обычно сопровождаются изменением как энтропии, так и энтальпии. Связь между энтальпией и энтропией системы устанавливает термодинамическая функция состояния, которая называется свободной энергией Гиббса или изобарно-изотермическим потенциалом (G). Она характеризует направление и предел самопроизвольного протекания процессов в изобарно-изотермических условиях (р = const и Т = const). С энтальпией и энтропией системы свободная энергия Гиббсасвязана соотношением

G = H – TS. (12)

Абсолютное значение измерить невозможно, поэтому используется изменение функции в процессе протекания того или иного процесса:

DG = DH – TDS. (13)

Свободная энергия Гиббса измеряется в кДж/моль и кДж. Физический смысл свободной энергии Гиббса: свободная энергия системы, которая может быть превращена в работу. Для простых веществ свободная энергия Гиббса принимается равной нулю.

Знак изменения свободной энергии Гиббса DG и ее величина при Р = const определяют термодинамическую устойчивость системы:

- если в химическом процессе происходит снижение свободной энергии Гиббса, т.е. DG < 0, процесс может протекать самопроизвольно, или говорят: процесс термодинамически возможен;

- если продукты реакции имеют больший термодинамический потенциал, чем исходные вещества, т.е. DG > 0, процесс протекать самопроизвольно не может, или говорят: процесс термодинамически невозможен;

- если DG = 0, то реакция может протекать как в прямом, так и в обратном направлении, т.е. реакция обратима.

Следовательно, самопроизвольные процессы при Р=const идут с уменьшением свободной энергии Гиббса. Этот вывод справедлив как для изолированных, так и для открытых систем.

Изменение энергии Гиббса системы при образовании 1 моль вещества из простых веществ, устойчивых в данных условиях, называется энергией Гиббса образования вещества DG_обр., измеряется в кДж/моль.

Если вещество находится в стандартных условиях, то энергия Гиббса образования называется стандартной энергией Гиббса образования вещества (DG⁰_обр.298). Стандартная энергия Гиббса образования простого вещества, устойчивого в стандартных условиях, равна нулю. Значения DG⁰_обр.298 веществ приводятся в справочниках.

Изменение энергии Гиббса, как и изменение энтальпии и энтропии, не зависит от пути процесса, поэтому изменение энергииГиббса химической реакции DG равно разности между суммой энергий Гиббса образования продуктов реакции и суммой энергий Гиббса образования исходных веществ с учетом стехиометрических коэффициентов:

DG⁰₂₉₈ = S(n_iDG 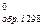)_пр. - S(n_iD G 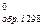)_исх.. (14)