Термодинамика электрохимических систем

При обратимом протекании в системе какого-нибудь процесса в изотермических условиях и при постоянном давлении связь между изменением энергии Гиббса (ΔG), энтальпии (ΔН) и энтропии (ΔS) дается уравнением

ΔG = ΔH – T ΔS

в котором TΔS есть изменение связанной энергии системы. При этом система представляется настолько большой, что переход ее от начального состояния к конечному не вызовет заметного изменения параметров. Например, в системе с химической реакцией начальные и конечные концентрации участников реакции можно считать одними и теми же. Если в системе идет процесс перехода вещества от большей концентрации к меньшей, то эти изменения происходят на бесконечно малую величину и т. д. Из термодинамики известно, что

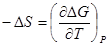
Тогда

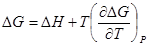
Это уравнение принято называть уравнением Гиббса — Гельм-гольца. Убыль энергии Гиббса электрохимической системы равна максимальной работе ΔА, которую может совершить система, а эта максимальная электрическая работа равна произведению напряжения системы на количество прошедшего электричества, т. е. zFE. Таким образом:

– ΔG = ΔA = zFE

Продифференцируем это выражение по температуре:

Следовательно, изменение энтропии можно определить из температурного коэффициента напряжения системы.

Подставив в уравнение Гиббса — Гельмгольца выражение убыли энергии Гиббса, получим

или

Так как изотермическая и обратимая электрическая работа является полным дифференциалом параметров Р, Т, то

и если Р = const, то

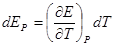
и полученное уравнение переписываем в виде:

В этом уравнении ΔН относится к количеству вещества, вступившему в реакцию при прохождении zF количества электричества, т. е. к одному молю.

Совершенно аналогичное выражение получается, если процесс идет изотермически и обратимо, но не при постоянном давлении, а при постоянном объеме. Тогда

ΔG_V = ΔH_V – TΔS и ΔS = – (∂ ΔG/∂T)_V

откуда

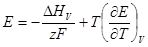или

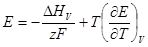
Электрическая работа, совершаемая системой, может быть больше, меньше или равна изменению энтальпии в зависимости от знака температурного коэффициента напряжения. Если (dE/dT)_P = 0, то

E = – ΔH/zF

и электрическая работа точно равна изменению энтальпии. Это уравнение называется уравнением Томсона. Его иногда применяют для ориентировочных расчетов напряжения.

При (dE/dT)_P < 0 электрическая работа, совершаемая системой, меньше изменения энтальпии и в изотермическом режиме часть тепловой энергии не превращается в электрическую работу, а рассеивается в виде теплоты. Когда же система отделена от окружающей среды теплонепроводящими стенками (адиабатические условия), то в процессе прохождения тока теплота не может рассеиваться и будет происходить нагревание системы.

Если (dE/dT)_P > 0, то электрическая работа больше изменения энтальпии и электрохимическая система в обратимом изотермическом режиме превращает в электрическую работу не только энергию, выделяющуюся при уменьшении энтальпии процесса, но и часть энергии окружающей среды. В адиабатическом режиме система, следовательно, будет охлаждаться.

В качестве примеров рассмотрим несколько электрохимических систем с водными и расплавленными электролитами (табл. 6.4).

Таблица 6.4. Проверка уравнения Гиббса — Гельмгольца

№ по пор.	Электрохимическая система	Химическая реакция в системе
1. 2. 3. 4. 5.	(–) Zn | ZnCl2 (aq), AgCl (тв.) | Ag (+) 0,535 кмоль/м3 (–) Pb | (CH3COO)2Pb (aq) || || (CH3COO)2Cu (aq) | Cu (+) (–) Hg | HgO, KOH || KCl, Hg2Cl2 | Hg (+) 0,01 кмоль/м3 0,01 кмоль/м3 (–) Pb | PbBr2 (расплав) | Br2 (C) (+) (–) Ag | AgCl (расплав) | Cl2 (C) (+)	Zn + 2AgCl (тв.) = = ZnCl2 + 2Ag Pb + (CH3COO)2Cu = = (CH3COO)2Pb + Cu Hg2Cl2 + 2KOH = = Hg2O + H2O + 2KCl Pb + Br2 = PbBr2 Ag + ½ Cl2 = AgCl

Система 1 обладает отрицательным температурным коэффициентом, и реакция в ней протекает с уменьшением энтальпии (экзотермическая реакция), которая из термохимических данных в условиях протекания реакции равна — 218,0 кДж/моль. Электрическая работа, которую может совершить система, меньше, чем ΔН. Расчет по формуле дает значение изменения энтальпии системы, очень близкое к определенному из термохимических измерений. В рассматриваемой электрохимической системе 90% выделяемой теплоты расходуется на совершение электрической работы, а 10% рассеивается или нагревает систему. Аналогичные соотношения имеем и для систем 4, 5. Рассчитанные из электрохимических измерений значения энтальпии совпадают с термохимическими данными в пределах ошибок опыта, а в электрическую работу превращается соответственно 73 и 82% от выделяющейся теплоты.

Температурный коэффициент напряжения системы 2 положителен. В соответствии с этим в электрическую работу превращается не только вся теплота, выделяющаяся при протекании реакции, но и часть теплоты (примерно 33%), поглощенной из окружающей среды. Значения энтальпии, определенные из электрохимических и термохимических измерений, хорошо согласуются друг с другом.

Наконец, в электрохимической системе 3 положителен не только температурный коэффициент напряжения, но и изменение энтальпии. Следовательно, эта система отбирает тепловую энергию от внешней среды не только для совершения электрической работы, но и на химическую реакцию.

Данные, приведенные в табл. 6.4, относятся к реакциям, протекающим не при стандартной температуре (298,15 К или 25°С). Для стандартных условий уравнение Гиббса — Гельмгольца должно быть записано в виде:

Т, К	z	E, B	, В/град	ΔG,	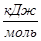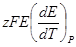,	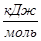ΔН, кДж/моль
из изме-рения напря-жения	из тер-мохи-мичес-ких данных
		1,015 0,476 0,164 1,100 0,913	– 4,02∙10–4 3,85∙10–4 0,84∙10–3 – 0,67∙10–3 – 0,29∙10–3	– 196,0 – 92,0 – 31,6 – 212,6 – 88,1	– 21,0 21,8 46,7 – 79,0 – 20,4	– 217,0 – 70,2 15,1 – 291,6 – 108,5	– 218,0 – 69,1 15,7 – 289,1 – 106,8

Здесь Е°, ΔН°, Т°, dE°/dT — величины, относящиеся к стандартным условиям.

Если же необходимо провести расчеты при каких-нибудь условиях, отличных от стандартных, то нужно знать ΔН и dE/dTдля этих условий. Рассмотрим сперва зависимости этих величин от температуры, считая, что активности участников реакции при всех температурах равны единице,

Вообще говоря, температурный коэффициент напряжения может изменяться с температурой, а также оставаться постоянным в значительном температурном интервале. Характер его изменения будет определяться изменением напряжения с температурой.

Продифференцируем уравнение Гиббса — Гельмгольца по температуре:

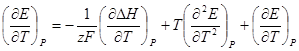
Из этого выражения следует, что

и если напряжение системы не зависит от температуры или линейно зависит от нее, то (∂²Е/∂∂Т²)_Р =0 и тогда

Но в соответствии с уравнением Кирхгоффа

где и 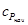— соответственно молярные теплоемкости при постоянном давлении конечных продуктов и начальных участников протекающего процесса.

Следовательно, для соблюдения условий независимости или линейного хода Е с температурой нужно, чтобы при протеканиипроцесса не происходило бы изменения теплоемкости системы, т. е. чтобы Δс_Р = 0. Тогда изменение напряжения с температурой будет происходить только вследствие изменения энтропии системы.

В рассматриваемом случае, поскольку изменение энтальпии не зависит от температуры, можно легко определить значение Е для любой температуры (Е_т), если только линейный ход Е с температурой соблюдается вплоть до этой температуры. Из выражения

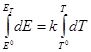
следует, что

Е_т = Е⁰ + k (Т – Т⁰)

где k — положительное или отрицательное значение температурного коэффициента.

Если же температурный ход напряжения системы не линейный, то напряжение системы определяется следующим образом. Определим изменение энтальпии при температуре Т(ΔН_Т) интегрированием уравнения Кирхгоффа:

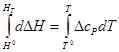
или

В случае какого-либо фазового превращения в системе в данном интервале температур нужно учесть также изменение энтальпии при этом превращении (ΔН_{ф. п}), т. е.

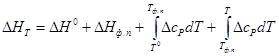
Теперь задача определения ΔН_Т может быть решена, если известен температурный ход теплоемкости каждого из участников реакции. В ряде случаев ход теплоемкости с температурой может быть выражен в виде ряда:

с_Р = с_Рº + аТ + bT² + cT³ + …

Тогда для Δс_Р аналогично

Δс_Р = Δс_Рº + ΔаТ + ΔbT² + ΔcT³ + …

Подставив это выражение в уравнение для ΔН_Т и проинтегрировав его в пределах от T⁰ до Т, получим:

При наличии в системе фазовых превращений ход рассуждений остается тем же, нужно только воспользоваться формулой для ΔН_Т, где учтено изменение энтальпии при фазовых превращениях.

Определение температурного коэффициента напряжения при температуре Т можно провести, воспользовавшись соотношением

из которого следует, что

Подставив вместо Δс_Р степенную зависимость и проведя интегрирование, окончательно получим изменение энтропии системы при интересующей нас температуре:

Разделив теперь ΔS_T на zF, получим температурный коэффициент и с помощью формулы Гиббса — Гельмгольца определим напряжение системы Е_T. Следует помнить, что Е_T относится к температуре Т и активностям участников реакции, равным единице.

Когда в реакции, протекающей в электрохимической системе, имеются газообразные участники, напряжение системы оказывается зависящим от давления. Для определения напряжения как функции давления (Е_Р) следует воспользоваться термодинамическим соотношением

(∂ΔG/∂P)_T = V

где V — изменение мольного объема при реакции.

Так как ΔG_V = – zFE, то

(∂ΔG_V/∂P)_T = – zF(∂E/∂P)_T

или

(∂E/∂P)_T = – V/zF

dE = – V dP/zF

Интегрирование этого выражения дает:

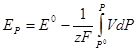
Если изменение объема подчиняется уравнению состояния идеального газа, то

и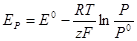

Здесь Е_P — напряжение системы при давлении Р, стандартной температуре и активностях всех конденсированных участников реакции, равных единице.

Если конденсированные участники реакции находятся не в стандартных состояниях, то это обстоятельство должно быть учтено при расчетах, но такие расчеты выходят за рамки книги.

Рассмотрим теперь формулу Гиббса — Гельмгольца применительно к системам без химической реакции.

В системах с электродами из разных модификаций одного и того же металла, например в системе

Sn (белое) | SnSO₄ | Sn (серое)

ΔH – изменение энтальпии при аллотропном переходе серого олова в белое. При температуре, отвечающей равновесию обеих модификаций, ΔG = 0 и, следовательно, Е = 0, откуда

ΔH = zFT(dE/dT)_P

т. е. все изменение энтальпии эквивалентно изменению связанной энергии системы.

Аналогичные рассуждения можно применить и к системам типа

М (жидкий) | Расплавленная соль | М (твердый)

(где М — металл), например

Рb (ж.) | РbС1₂ | Pb (тв.)

при температуре плавления. Поскольку при плавлении энтальпия изменяется, то, на первый взгляд, можно было ожидать, что при замыкании такой системы потечет ток и произойдут процессы растворения жидкого металла и восстановления ионов металла на твердом электроде. Однако такое заключение ошибочно, ибо при температуре плавления ΔG = 0 и вся теплота, затрачиваемая на плавление, идет на увеличение связанной энергии системы. Следовательно, в этом случае напряжение системы равно нулю и она не может совершить работы.

В остальных типах систем без химической реакции никаких превращений не происходит, а электрическая работа совершается в результате переноса энергии от более высокого уровня к менее высокому уровню. Поскольку в случае идеальных систем внутренняя энергия U не зависит от объема, то ΔH = 0 и

E=T(dE/dT)_P

Следовательно, электрическая работа в таких системах совершается только вследствие изменения связанной энергии. Преобразовав это уравнение

dE/E = dT/T

можем написать

d ln E = dlnT

откуда после интегрирования имеем

ln E = ln Т + const и E = k’T

В идеальных электрохимических системах данного типа напряжение, таким образом, прямо пропорционально абсолютной температуре.

В реальных же системах (∂U/∂V)_P ≠ 0 и ΔH в формуле Гиббса — Гельмгольца будет равно энтальпии перехода моля вещества от уровня с большей энергией на уровень с меньшей энергией. Например, в системах типа

(–) М | МА || МА | М (+)

a₁ а₂

ΔH — изменение энтальпии при переходе моля растворенного электролита от активности а₂ к активности а₁, т. е. энтальпия разведения в данных пределах (а₂ > a₁).

В указанного типа электрохимической системе не всегда удается достаточно полно элиминировать скачок потенциала на границе двух жидких фаз. Поэтому удобнее воспользоваться двумя одинаковыми электрохимическими системами с химическими реакциями, в одной из которых активность электролита равна а₁, а в другой — a₂, и включить их в измерительную цепь напротив друг другу таким образом, чтобы слева находилась система с большим напряжением:

(–) (Pt) H₂ | HCl, AgCl (тв.) | Ag — Ag | AgCl (тв.), НС1 | H₂ (Pt) (+)

a₁ a₂

Измеренное напряжение E_p = E₁ – E₂ и, следовательно,

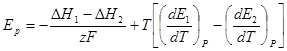
При небольших разностях концентраций разность температурных коэффициентов очень невелика, и таким путем из измерений напряжения можно прямо рассчитать энтальпию разведения от активности а₂ до а₁.

ИОНОСЕЛЕКТИВНЫЕ ЭЛЕКТРОДУ