Связь диффузионного потенциала с числами переноса

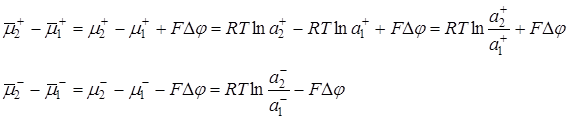
В стационарных условиях

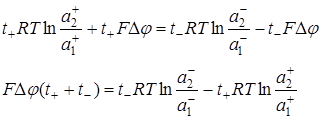
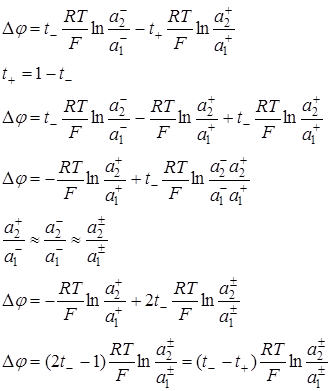
Методы определения чисел переноса

Метод Гитторфа

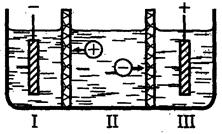
· пропускаем 1 Фарадей электричества

· на катоде осаждается 1 моль-экв меди

· из отсека 2 в 3 выйдет t₊ моль-экв Cu²⁺. Убыль Cu²⁺ вблизи катода Δn = (1– t₊) = t_– моль-экв

· из отсека 1 в 2 мигрирует t_– моль-экв SO₄^2–

· Следовательно электронейтральность раствора сохранена

1 моль-экв –––– F

Δn ––––––––––– t_– Q

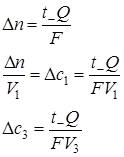
Метод движущейся границы

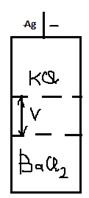
Сущность – определение расстояния, на которое переместится под действием тока граница между растворами. Используется в показателях преломления.

· берут соли с общим анионом

· t (Ba²⁺) < t (K⁺)

· концентрации подбирают

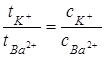
Если прошло Q Кл, то количество электричества, перенесенное K⁺ равно t₊Q. Этот заряд равен заряду всех K⁺, находящихся в объеме V

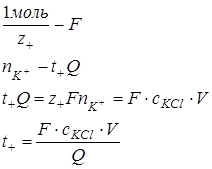
Предельные электропроводности электролитов

Предельные эквивалентные электропроводности и предельные числа переноса позволяют определить предельные электропроводности электролитов

Закономерности:

1) рост λ_i^∞ с ростом температуры ( в отличие от металлов)

2) наличие максимумом на кривых λ_i^∞ ­– радиус иона (кристаллографически)

Гидродинамическая модель проводимости растворов электролитов

Для количественной интерпретации наблюдаемых закономерностей проводят аналогию между перемещением иона под действием электрического поля и действием макроскопического шарика в водной жидкости.

Согласно закону Стокса, скорость движения твердого шарика в водной жидкости и сила трения связаны

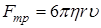
r – радиус шарика, η – вязкость

Величина λ_i^∞ определяется двумя видами воздействия на ион: стоковской силой внутреннего трения и эл. силой.

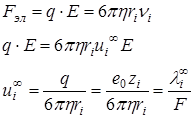
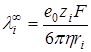– уравнение Стокса для определения радиусом сольватированных ионов (r_i)

Правило Вальдена-Писаржевского

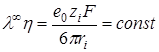
· Правило справедливо в узком температурном интервале в силу зависимости радиуса сольватированного иона от температуры

· При низких концентрациях величина радиуса иона становится постоянной, так как сольватация достигает своего предела.

Уравнение Стокса-Эйнштейна

Значение предельных электропроводностей ионов используется для расчета точных значений коэффициента диффузии

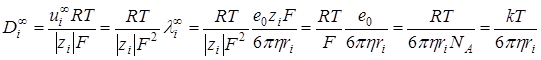
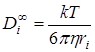(Уравнение Стокса-Эйнштейна. Связывает коэффициент диффузии и радиус сольватного иона)

Определение растворимости и ПР труднорастворимых солей

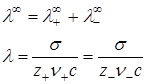( с – растворимость)

σ (измеряемая) = σ (соли) + σ (воды)

Основы теории Дебая-Хюккеля-Онзагера

Кольрауш: λ = λ^∞ – а *с^1/2

Характер электропроводимости растворов электролитов был объяснен Онзагером с помощью т. Д.-Х.

Онзагер постулировал, что взаимодействие ионов вызывает появление 2 эффектор торможения:

Электрофоретического

Релаксационного

1) Электрофоретический.Связан с тем, что центральный ион и его ионная атмосфера движутся в электронном поле навстречу друг другу.

Сила вязкого трения оказывается повышенной по сравнению со случаем неподвижного растворителя, так как ион движется не в неподвижной среде, а в среде передвигающейся в противоположном направлении. Это снижает эквивалентную электропроводность на некоторую λ_эф.

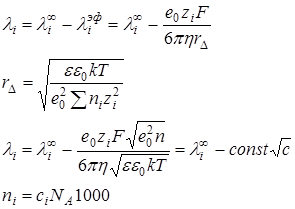
Релаксационный эффект

При перемещении под действием электрического поля ион выходит из центра ионной атмосферы, которая при движении иона не успевает перестроиться (релаксировать). Следовательно, при движении иона она становится ассиметричной по отношению к иону.

Асимметрия ионной атмосферы снижает эквивалентную электропроводность на некоторую λ_рел.

С учетом 2 эффектов снижение эквивалентной электропроводности состоит:

λ = λ^∞ – λ_эф – λ_ред

Эффект Вина

· При кратковременных импульсах тока в сильных полях электропроводность раствора электролита растет и достигает предельного значения, соответствующего λ^∞

· Причина – при большой напряженности электрического поля скорость движения иона будет велика, поэтому ионная атмосфера не будет успевать образовываться (тормозящие эффекты будут отсутствовать)

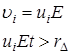
Можно рассчитать напряженность электрического поля.

Для слабых электролитов эффект Вина выражен сильнее – происходят диссоциация слабого электролита под действием электрического поля.