Основные типы задач на химическое равновесие

Существует два основных типа задач, связанных с расчётом параметров равновесной системы:

1) известны начальные концентрации исходных веществ, необходимо найти равновесные концентрации и константу равновесия;

2) известны начальные концентрации исходных веществ и константа равновесия, необходимо определить равновесные концентрации всех веществ.

Для решения подобных задач необходимо понимать, что равновесную концентрацию любого исходного вещества можно найти, отняв от его начальной концентрации концентрацию вступившего в реакцию вещества.

Если до начала реакции в системе находились только исходные реагенты, то концентрация вещества, образовавшегося к моменту наступления равновесия в результате протекания реакции, представляет собой равновесную концентрацию продукта реакции. Если же в систему до начала реакции было введено извне некоторое количество продукта реакции, то его равновесную концентрацию находят, суммируя концентрацию продукта до реакции и концентрацию продукта, образовавшегося к моменту наступления равновесия в результате протекания реакции. Для определения количества (или концентрации) прореагировавшего и образовавшегося веществ обычно проводятся стехиометрические расчёты по уравнению реакции.

Пример 1. Начальные концентрации водорода и йода в равновесной системе равны 3 моль/л и 4 моль/л соответственно.:

H_{2 (газ)} + I_{2 (газ)} ⇆ 2 HI _(газ)

К моменту наступления химического равновесия концентрация йодоводорода в системе составила 1 моль/л. Определить константу равновесия данной реакции.

Для того чтобы рассчитать константу равновесия, необходимо сначала рассчитать равновесные концентрации всех участников реакции и затем подставить их в выражение константы равновесия

.

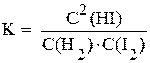Равновесная концентрация йодоводорода, как это следует из условия задачи, равна 1 моль/л. Если известно, что к моменту наступления равновесия образовалось 1 моль/л HI, то из уравнения реакции следует, что и водорода, и йода прореагировало в два раза меньше, т.е. по 0,5 моль/л. Таким образом, равновесные концентрации йода и водорода будут следующими:

С_равн.(H₂)= C_нач.(H₂) - C_{прореаг.}(H₂) = 3 моль/л - 0,5 моль/л = 2,5 моль/л;

С_равн.(I₂)= C_нач.(I₂) - C_{прореаг.}(I₂) = 4 моль/л - 0,5 моль/л = 3,5 моль/л.

Так как С_равн.(HI) = 1 моль/л, константа равновесия равна

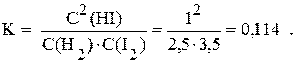
Пример 2. Рассчитать равновесные концентрации водорода, йода и йодоводорода в системе H_{2 (газ)} + I_{2 (газ)} ⇆ 2 HI _(газ), если известно, что начальные концентрации H₂ и I₂ равны 5 моль/л и 3 моль/л соответственно, а константа равновесия равна 1.

В условии задачи ничего не говорится о концентрациях прореагировавших исходных веществ и образовавшихся продуктов. Поэтому при решении таких задач обычно концентрация какого-нибудь прореагировавшего вещества принимается за x «икс». Пусть к моменту наступления равновесия прореагировало x моль/л водорода, тогда из уравнения реакции следует, что йода должно прореагировать тоже x моль/л, а йодоводорода должно образоваться 2x моль/л. Равновесные концентрации всех участников реакции будут следующими:

С_равн.(H₂) = C_нач.(H₂) - C_{прореаг.}(H₂) = (5 - x) моль/л;

С_равн.(I₂) = C_нач.(I₂) - C_{прореаг.}(I₂) = (3 - x) моль/л;

С_равн.(HI) = 2x моль/л.

Подставляя выраженные через икс равновесные концентрации в выражение константы равновесия, и, решая полученное уравнение, можно найти x и равновесные концентрации.

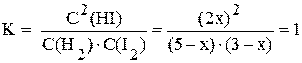
3x² + 8x - 15 = 0

x₁ = -3,94 x₂ = 1,27

Физический смысл имеет только положительный корень x = 1,27. Следовательно:

С_равн.(H₂) = (5 - x) моль/л = 5 - 1,27 = 3,73 моль/л;

С_равн.(I₂) = (3 - x) моль/л = 3 - 1,27 = 1,73 моль/л;

С_равн.(HI) = 2x моль/л = 2·1,27 = 2,54 моль/л.