Капля жидкости в насыщенном паре

В насыщенном паре образовалась капля жидкости радиусом R. Найти условия увеличения и уменьшения размера капли. Аналогичная задача возникает для квантовой точки, образующейся в насыщенном растворе.

При образовании капли происходит переход N частиц пара в жидкость. Для этого химический потенциал пара должен превышать химический потенциал жидкости . При изотермическом и изохорическом образовании капли система равновесная при минимуме свободной энергии 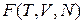. Из (2.67) с учетом энергии поверхностного натяжения капли получаем

,

где

– площадь поверхности капли радиусом R;

s – коэффициент поверхностного натяжения.

Изменение свободной энергии при образовании капли

,

где

– число частиц жидкости в капле;

v – объем одной частицы.

Размер капли не меняется в равновесной системе. Это требует экстремума свободной энергии

.

Используем

,

получаем равновесный радиус капли

. (П.7.16)

С учетом

выполняется

.

Следовательно, свободная энергия максимальна. Устойчивое равновесие соответствует минимуму свободной энергии, поэтому в рассматриваемом случае состояние капли неустойчиво:при капля увеличивается; при капля испаряется.

Как изменится состояние капли, если она образуется вокруг иона?

Заряженная капля в насыщенном паре

Ион радиусом R_I имеет заряд q, его окружает пар c химическим потенциалом . Вокруг иона образовалась капля жидкости радиусом R c химическим потенциалом m₂.

Используем обозначения и результаты примера 3. Дополнительно учитываем энергию электрического поля капли

,

где

– электрическая энергия единицы объема;

e – диэлектрическая проницаемость жидкости;

– напряженность поля внутри капли при ;

– напряженность поля вне капли.

Изменение свободной энергии при образовании капли равно

= .

При достаточно большом заряде и малом размере иона главную роль играет третье слагаемое. Оно отрицательное и уменьшается с увеличением R. При уменьшении свободной энергии возрастает устойчивость системы. В результате заряженная капля увеличивается даже в ненасыщенном паре.

Если капля получает заряд за счет эмиссии электронов, то, как показал Джон У. Рэлей в 1882 г., при достаточно малом размере R₀ ~ 50 мкм, называемом пределом Рэлея, капля становится неустойчивой из-за преобладания сил электростатического отталкивания над поверхностным натяжением. Капля вытягивается, из ее концов выбрасывается заряд, переносимый струями жидкости.

Вопросы коллоквиума

1. Фазовое пространство для идеального газа. Микросостояние и макросостояние. Фазовый ансамбль. Число степеней свободы. Число микросостояний. Плотность микросостояний фазового ансамбля. Теорема Лиувилля.

2. Каноническое распределение. Условие применимости. Статистический интеграл. Свободная энергия. Применение к идеальному газу. Статистический интеграл поступательного движения частицы.

3. Распределение энергии частицы по степеням свободы для гамильтониана со степенными зависимостями. Неустранимая погрешность измерительного прибора с упругой силой.

4. Распределение Максвелла по модулю скорости и по энергии для концентрации частиц. Наиболее вероятные и средние значения.

5. Распределение Больцмана по координатам для концентрации частиц. Формула Больцмана для однородного поля тяжести.

6. Термодинамические потенциалы. Внутренняя энергия. Химический и электрохимический потенциал. Условие равновесия системы. Химический потенциал и статистический интеграл. Зависимости химического потенциала.

Вопросы экзамена

1. Биномиальное распределение. Дробовой шум.

2. Статистическое описание системы частиц в фазовом пространстве. Функция распределения. Теорема Лиувилля.

3. Микроканоническое распределение. Энергетическая плотность состояний. Термодинамические величины. Вычисление плотности состояний идеального газа.

4. Каноническое распределение. Статистический интеграл. Термодинамические величины. Вычисление статистического интеграла поступательного движения.

5. Распределение энергии по степеням свободы. Неустранимая погрешность измерительного прибора. Закон Дюлонга и Пти.

6. Распределение энергии по степеням свободы. Флуктуационная ЭДС в активном сопротивлении.

7. Распределение Максвелла по скорости и по энергии. Средние значения скоростей и энергии.

8. Плотность потока частиц, плотность потока энергии.

9. Термоэлектронная эмиссия. Формула Ричардсона.

10. Распределение Больцмана. Газ в центрифуге.

11. Распределение Больцмана. Поляризация диэлектрика.

12. Термодинамические характеристики системы с переменным числом частиц. Химический потенциал и его вычисление для идеального газа.

13. Распределение Максвелла–Больцмана по состояниям.

14. Большое каноническое распределение. Выражения для термодинамических характеристик.

15. Трудности классической статистической физики. Полуклассическая квантовая механика. Квантование одномерной системы. Условия применимости классической статистической физики.