Химические равновесия в биологических системах

Анализ химических равновесий играет значительную роль при решении биохимических проблем. Как правило, в этих целях используют термодинамический подход. Это действительно удобно, так как термодинамический аппарат дает возможность анализировать только начальное и конечное состояние без учета интермедиатов (промежуточных продуктов), число которых может составлять несколько десятков.

С другой стороны, если сложную биологическую систему трудно описывать при помощи термодинамических средств, то её разделяют на более простые компоненты. Важные составные части, поддаю-щиеся термодинамическому анализу, включают в себя:

1) метаболические реакции;

2) кислотно-основные равновесия;

3) окислительно-восстановительные реакции;

4) ионные процессы;

Суть термодинамического анализа заключается в следующем: по термодинамическим характеристикам (DH⁰, DS⁰, DG⁰) определяют значение константы равновесия, которое в дальнейшем используют для расчета равновесного состава системы. Иногда решают обратную задачу: проводят химический анализ биологической системы (клетки, мышцы и т. д.), по закону действующих масс рассчитывают величины констант имеющихся химических равновесий, по которым, в свою очередь, рассчитывают термодинамические величины.

Рассмотрим некоторые примеры.

Пример 5.Одной из стадий метаболизма глюкозы является реакция изомеризации глюкозо-6-фосфата во фруктозо-6-фосфат:

глюкозо-6-фосфат ⇄ фруктозо-6-фосфат ΔG⁰ = 1,7 кДж/моль.

Определить, является ли реакция практически обратимой (или необратимой) при 37⁰С, указать направление смещения равновесия и рассчитать степень превращения.

Решение.

По формуле (30) рассчитаем константу равновесия:

;

.

Так как значение K < 1 (но не << 1), то реакция является практически обратимой, а равновесие при стандартных условиях смещено влево.

Обозначим исходное количество (молярную концентрацию) и количество прореагировавшего глюкозо-6-фосфата за «а» и «х» соответственно. Тогда:

[фруктозо-6-фосфат] = x;

[глюкозо-6-фосфат] = а - x.

Подставим переменные в выражение для K:

.

Решая это уравнение, найдем:

Таким образом, только 34% глюкозо-6-фосфата подвергается изомеризации.

Формулы, связывающие степень превращения (выход) с константой равновесия, для реакций различных типов, приведены в таблице 3.

Пример 6.Фермент альдолаза катализирует переход фруктозо-1,6-дифосфата (ФДФ) в дигидроацетонфосфат (ДГАФ) и глицеральдегид-3-фосфат (ГАФ), протекающий обратимо по уравнению:

ФДФ ⇄ ДГАФ + ГАФ

В физиологических условиях (t⁰ » 37⁰C) концентрации этих соединений в эритроцитах составляют: C (ФДФ) = 35 мкмоль/л; C (ДГАФ) = 130 мкмоль/л; C (ГАФ) = 15 мкмоль/л. Определить направление самопроизвольного протекания процесса в данных условиях, если ΔG⁰ = 23,8 кДж/моль.

Решение.

Запишем для данной реакции уравнение изотермы Вант-Гоффа:

Таким образом, в реальных условиях ΔG < 0 и реакция будет самопроизвольно протекать в прямом направлении.

Таблица 3. Формулы для расчета степени превращения[14].

Уравнение реакции		Уравнение реакции	х
A ⇄ B		A ⇄ 2B
A + B ⇄ C + D		A ⇄ B + С
A + B ⇄ 2C		A + B ⇄ C

а - исходное количество (молярная концентрация) реагентов;

x - количество (молярная концентрация) прореагировавшего вещества;

K - константа равновесия.

Примеры решения задач

Задача №1

При определённых условиях в системе установилось равновесие:

2А + B ⇄ 2C.

Равновесные концентрации веществ составили: [A] = 4 моль/л; [B] = 6 моль/л; [C] = 12 моль/л. Определить:

1) значение константы равновесия;

2) является ли при данных условиях реакция практически обратимой (или необратимой);

3) направление смещения равновесия;

4) исходные концентрации веществ A и B.

Решение.

Значение константы равновесия найдем через закон действующих масс:

Так как 1 < K_C < 10⁵, то реакция является практически обратимой и равновесие смещено вправо.

Исходные концентрации равны сумме равновесных концентраций и концентраций вступивших в реакции веществ. Последние можно определить из стехиометрических соотношений:

С(A)_{прореаг.} = [C] = 12 моль/л;

С(B)_{прореаг.} = = 6 моль/л.

Отсюда:

С₀(A) = [A] + С(A)_{прореаг.} = 4 + 12 = 16 моль/л;

С₀(B) = [B] + С(B)_{прореаг.} = 6 + 6 = 12 моль/л.

Задача №2

Реакция образования йодистого водорода протекает по уравнению:

H_2(газ) + I_2(газ) ⇄ 2HI_(газ).

Исходные концентрации веществ: С₀(H₂) = 0,02 моль/л; С₀(I₂) = 0,04 моль/л. Известно, что равновесие в системе установилось, когда в реакцию вступило 50% Н₂. Вычислить константу химического равновесия и определить направление смещения равновесия при:

1) увеличении концентрации I₂;

2) уменьшении концентрации HI;

3) увеличении давления.

Решение.

Исходя из уравнения реакции, определяем концентрации веществ, прореагировавших между собой:

С(H₂)_{прореаг.} = 0,5·0,02 = 0,01 моль/л;

С(I₂)_{прореаг.} = С(H₂)_{прореаг.} = 0,01 моль/л.

Находим равновесные концентрации:

[HI] = 2×С(H₂)_{прореаг.} = 0,02 моль/л (по уравнению реакции);

[H₂] = С₀(H₂) - С(H₂)_{прореаг.} = 0,02 - 0,01 = 0,01 моль/л;

[I₂] = С₀(I₂) - С(I₂)_{прореаг.} = 0,04 - 0,01 = 0,03 моль/л.

Подставляем равновесные концентрации в выражение для константы равновесия:

Увеличение концентрации I₂ и уменьшение концентрации HI приведет к сдвигу равновесия в направлении прямой реакции. Увеличение давления не вызовет сдвига равновесия, так как число моль газов в левой и правой частях уравнения одинаково.

Задача №3

При определённых условиях константа равновесия реакции:

CO_2(газ) + H_2(газ) ⇄ CO_(газ) + H₂O_(пар)

равна 1.

Исходные концентрации СO₂ и H₂ составили соответственно 0,2 моль/л и 0,8 моль/л. Рассчитать равновесный состав системы.

Решение.

Обозначим концентрации С(СО₂) и С(Н₂), вступивших в реакцию, через «х». Тогда:

[СO₂] = [H₂O] = x;

[СO₂] = 0,2 - х;

[H₂] = 0,8 - х.

Запишем выражение для константы равновесия:

x² = 0,16 - 0,2x - 0,8x + x²

x = 0,16.

Равновесные концентрации всех веществ равны:

[СO] = [H₂O] = 0,16 моль/л;

[СO₂] = 0,2 - 0,16 = 0,04 моль/л;

[H₂] = 0,8 - 0,16 = 0,64 моль/л.

Задача №4

Рассчитать константу химического равновесия K_С для реакции:

NO_2(газ) + SO_2(газ) ⇄ NO_(газ) + SO_3(жидк.)

по известным данным:

	NO2	SO2	NO	SO3
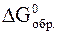, кДж/моль		–300		–370

Определить является ли реакция практически обратимой (или необратимой) при 25⁰С.

Решение.

Рассчитаем стандартную энергию Гиббса реакции по первому следствию из закона Гесса:

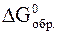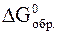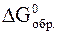= SО₃ + NO - NO₂ - 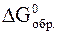SO₂ = -32 кДж.

< 0, следовательно, процесс самопроизвольно протекает в прямом направлении.

Величину K_C найдем по уравнению (30¢¢¢):

K_C > 10⁵, т. е. при данной температуре реакция является практически необратимой.

Задача №5

Для реакции: фумарат + H₂O ⇄ малат значения константы равновесия при 25⁰С и 35⁰С равны соответственно 4 и 8.

Рассчитать:

1) стандартную энтальпию реакции;

2) константы равновесия при 30⁰С.

Решение.

Стандартную энтальпию рассчитаем по уравнению изобары химической реакции (33):

Примем T₁ = 298 K, T₂ = 303 K и преобразуем уравнение (33):

.

Отсюда:

Вопросы для самоконтроля

1. Какие реакции называют обратимыми? Какие необратимыми? Приведите примеры.

2. Что называется химическим равновесием? Сформулируйте термодинамическое и кинетическое определение состояния химического равновесия.

3. Прекращаются ли реакции после наступления равновесия?

4. Как формулируется закон действующих масс для обратимой реакции?

5. Концентрации каких фаз входят в выражение закона действующих масс для обратимой реакции?

6. Что такое константа равновесия?

7. От каких факторов зависит и от каких не зависит константа равновесия?

8. Может ли K быть равной нулю?

9. Какова взаимосвязь между K_С и K_P?

10. Сформулируйте принцип Ле Шателье. Какие факторы влияют на химическое равновесие?

11. Сформулируйте частные принципы смещения равновесия при изменении температуры, концентрации, давления.

12. Смещает ли равновесие в системе введение в неё катализатора?

Варианты задач для самостоятельного решения

*Для расчета степени превращения можно воспользоваться формулами, приведёнными в таблице 3.

Вариант №1

1. Реакция взаимодействия азота с водородом протекает по уравнению: N₂ + 3H₂ ⇄ 2NH₃. В состоянии равновесия концентрации веществ оказались равны: [N₂] = 0,8 моль/л; [H₂] = 1,2 моль/л; [NH₃] = 1,6 моль/л. Определить:

1) величину константы равновесия;

2) является ли при данных условиях реакция практически обратимой (или необратимой);

3) направление смещения равновесия при данных условиях;

4) исходные концентрации веществ A и B.

2. Ключевой ступенью в биосинтезе триацилглицеринов (жиров) является переход глицерина в глицерин-1-фосфат при помощи АТФ:

глицерин + АТФ ⇄ глицерин-1-фосфат + АДФ

В устойчивом состоянии в живой клетке [АТФ] = 10^-3 моль/л и [АДФ] = 10^-4 моль/л. Найти соотношение глицерин/глицерин-1-фосфат, если K_C = 1,8.

3. Первой стадией метаболизма глюкозы является реакция:

глюкоза + АТФ ⇄ глюкозо-6-фосфат + АДФ,

для которой ΔG⁰ = -16,7 кДж/моль.

Определить, является ли реакция практически обратимой (или необратимой) при 37⁰С, указать направление смещения равновесия и рассчитать степень превращения, при условии равенства начальных концентраций глюкозы и АТФ.

Вариант №2

1. Константа равновесия для реакции: A + B ⇄ C + D при 80⁰С равна 1. Исходные концентрации веществ A и B составили соответственно 2 и 6 моль/л. Рассчитать равновесный состав системы.

2. Муравьиная кислота диссоциирует в растворе по уравнению:

HCOOH ⇄ HCOO^- + H⁺.

Рассчитать константу равновесия, если начальная концентрация кислоты равна 0,05 моль/л, а концентрация формиат-ионов в состоянии равновесия составляет 0,005 моль/л.

3. Для реакции трансаминирования:

глутамат + пируват ⇄ α-кетоглутарат + аланин

при 300 K константа равновесия равна 1,11.

Определить направление протекания реакции, если:

С(глутамат) = С(пируват) = 0,000025 моль/л;

С(α-кетоглутарат) = С(аланин) = 0,005 моль/л.

Вариант №3

1. Реакция протекает по уравнению: A + B ⇄ 2C. Начальные концентрации веществ A и B составляли соответственно 3 и 6 моль/л. На момент наступления химического равновесия в реакцию вступило 30% A. Определить:

1) величину константы равновесия;

2) является ли при данных условиях реакция практически обратимой (или необратимой);

3) направление смещения равновесия при данных условиях.

2. В водном растворе фермент фумараза позволяет достичь равновесия:

фумарат + H₂O ⇄ малат,

которое устанавливается при избытке воды.

При 35⁰С константа равновесия равна 8. Найти начальную концентрацию фумарата, если равновесная концентрация малата составила 0,04 моль/л.

3. Стандартная энергия Гиббса (ΔG⁰) для реакции гидратации цис-аконитовой кислоты, протекающей по уравнению:

цис-аконитат + H₂O ⇄ изоцитрат,

составляет -1,68 кДж/моль.

Рассчитать константу равновесия этой реакции и сделать вывод о практической обратимости этой реакции при 37⁰С. Определить степень превращения, считая концентрацию воды постоянной.

Вариант №4

1. В состоянии химического равновесия в системе: 2A + B ⇄ 2C концентрации веществ составили: [A] = 5 моль/л; [B] = 3 моль/л; [С] = 8 моль/л. Определить:

1) величину константы равновесия;

2) является ли при данных условиях реакция практически обратимой (или необратимой);

3) направление смещения равновесия при данных условиях;

4) исходные концентрации веществ A и B.

2. Пировиноградная кислота диссоциирует в растворе по уравнению:

CH₃COCOOH ⇄ CH₃COCOO^- + H⁺.

Рассчитать константу равновесия, если начальная концентрация кислоты равна 0,05 моль/л, а концентрация пируват-ионов в состоянии равновесия составляет 0,016 моль/л.

3. Важной реакцией при зрительном возбуждении является гидролиз гуанозинтрифосфата (ГТФ):

ГТФ + H₂O ⇄ ГДФ + фосфат,

протекающий при избытке воды.

При 37⁰С константа равновесия равна 2·10³. Определить направление протекания процесса при следующих концентрациях веществ: С(ГТФ) = 0,5 ммоль/л; С(ГДФ) = 5 ммоль/л; С(фосфат) = 15 ммоль/л.

Вариант №5

1. Константа равновесия для реакции: A + B ⇄ 2C равна 4. Исходные концентрации веществ A и B составили соответственно 3 и 6 моль/л. Рассчитать равновесный состав системы.

2. В печени протекает обратимый процесс:

глюкозо-6-фосфат ⇄ фруктозо-6-фосфат.

Найти константу равновесия, если исходная концентрация глюкозо-6-фосфата равна 0,05 моль/л, а равновесная концентрация фруктозо-6-фосфата составила 0,0475 моль/л.

3. Стандартная энергия Гиббса (ΔG⁰) для реакции гидролиза глицил-глицина, протекающей при избытке воды по уравнению:

глицил-глицин + H₂O ⇄ 2 глицин

составляет -15 кДж/моль.

Рассчитать константу равновесия этой реакции и сделать вывод о практической обратимости этой реакции при 37⁰С. Определить степень превращения, приняв начальную концентрацию глицил-глицина равной 0,01 моль/л.

Вариант №6

1. Реакция протекает по уравнению: A + B ⇄ 2C. Начальные концентрации веществ A и B составляли соответственно 2 и 4 моль/л. На момент наступления химического равновесия в реакцию вступило 40% A. Определить:

1) величину константы равновесия;

2) является ли при данных условиях реакция практически обратимой (или необратимой);

3) направление смещения равновесия при данных условиях.

2. Второй стадией метаболизма глюкозы является реакция:

глюкозо-1-фосфат ⇄ фруктозо-1-фосфат,

константа равновесия которой при 25⁰С равна 0,5. Найти выход фруктозо-1-фосфата (степень превращения глюкозо-1-фосфата), если исходная концентрация глюкозо-1-фосфата равна 0,1 моль/л.

3. При определённых условиях константа равновесия реакции этерификации, протекающей по уравнению:

CH₃COOH + C₂H₅OH ⇄ CH₃COOC₂H₅ + H₂O,

равна 4.

Определить направление протекания процесса при следующих концентрациях веществ: С(CH₃COOH) = C(CH₃COOH) = 0,25 моль/л; С(CH₃COOC₂H₅) = 0,5 моль/л; С(H₂O) = 2 моль/л.

Вариант №7

1. Равновесие в реакции: C₂H₂ + 2H₂ ⇄ C₂H₆ установилось при концентрациях веществ: [C₂H₂] = 2 моль/л; [H₂] = 3 моль/л; [C₂H₆] = 8 моль/л. Определить:

1) величину константы равновесия;

2) является ли при данных условиях реакция практически обратимой (или необратимой);

3) направление смещения равновесия при данных условиях;

4) исходные концентрации веществ A и B.

2. Для реакции 2NO₂ ⇄ N₂O₄ при 25⁰С константа равновесия равна 210. Вычислить значение константы равновесия при 40⁰С, если стандартная энтальпия реакции равна -57,4 кДж/моль.

3. Стандартная энергия Гиббса (ΔG⁰) для реакции окисления этанола в уксусный альдегид, протекающей по уравнению:

C₂H₅OH + 0,5O₂ ⇄ CH₃CHO + H₂O

составляет -190 кДж/моль. Рассчитать константу равновесия этой реакции и сделать вывод о практической обратимости этой реакции при 25⁰С. Определить степень превращения, считая концентрацию воды постоянной.

Вариант №8

1. Константа равновесия для реакции: 2A + B ⇄ 2C равна 2. Исходные концентрации веществ A и B составили соответственно 10 и 5 моль/л. Рассчитать равновесный состав системы.

2. Уксусная кислота диссоциирует в растворе по уравнению:

CH₃COOH ⇄ CH₃COO^- + H⁺.

Рассчитать константу равновесия, если начальная концентрация кислоты равна 0,05 моль/л, а концентрация ацетат-ионов в состоянии равновесия составляет 0,0001 моль/л.

3. Для реакции гидролиза АТФ, протекающего по уравнению:

АТФ + H₂O ⇄ АДФ + Фосфат,

при 37⁰С константа равновесия равна 2,3·10⁵.

Определить направление протекания процесса в эритроцитах, если концентрации фосфата и АТФ превышают концентрацию АДФ, равную 2,5·10^-5 моль/л, в 8 и 13 раз соответственно, а вода присутствует в значительном избытке.

Вариант №9

1. Реакция протекает по уравнению: A + B ⇄ 2C. Начальные концентрации веществ A и B составляли соответственно 3 и 5 моль/л. На момент наступления химического равновесия образовалось 2 моль/л вещества С. Определить:

1) величину константы равновесия;

2) является ли при данных условиях реакция практически обратимой (или необратимой);

3) направление смещения равновесия при данных условиях.

2. Константа равновесия процесса изомеризации 3-фосфо-глицерата в 2-фосфоглицерат при 20 и 30⁰С составляет соответственно 0,1558 и 0,1569. Найти стандартную энтальпию реакции.

3. Третьей стадией гликолиза является реакция:

фруктозо-6-фосфат + АТФ ⇄ фруктозо-1,6-дифосфат + АДФ,

для которой ΔG⁰ = -14,2 кДж/моль.

Рассчитать константу равновесия этой реакции и сделать вывод о практической обратимости этой реакции при 25⁰С. Определить степень превращения при условии равенства начальных концентраций фруктозо-6-фосфата и АТФ.

Вариант №10

1. Константа равновесия для реакции: A + B ⇄ C + D равна 1. Исходные концентрации веществ A и B составили 2 моль/л, а веществ C и D - 1 моль/л. Рассчитать равновесный состав системы.

2. Константа равновесия реакции:

глутамат + пируват ⇄ кетоглутарат + аланин

при 25⁰С равна 1,5. Найти соотношение аланин/пируват, если равновесные концентрации глутамата и кетоглутарата равны соответственно 10^-3 и 10^-2 моль/л.

3. На четвертой стадии гликолиза фруктозо-6-фосфат распадается на дигидроксиацетонфосфат и глицеральдегид-3-фосфат. Константа равновесия этого процесса равна 10^-4. Определить направление самопроизвольного протекания процесса в физиологических условиях (t⁰ » 37⁰C), если концентрации этих соединений составляют: C (фруктозо-6-фосфат) = 45 мкмоль/л; C (дигидроксиацетонфосфат) = 120 мкмоль/л; C (глицеральдегид-3-фосфат) = 20 мкмоль/л.

Вариант №11

1. В состоянии химического равновесия в системе: A + B ⇄ 2C концентрации веществ составили: [A] = 2 моль/л; [B] = 4 моль/л; [С] = 8 моль/л. Определить:

1) величину константы равновесия;

2) является ли при данных условиях реакция практически обратимой (или необратимой);

3) направление смещения равновесия при данных условиях;

4) исходные концентрации веществ A и B.

2. Молочная кислота диссоциирует в растворе по уравнению:

CH₃CH(OH)COOH ⇄ CH₃CH(OH)COO^- + H⁺.

Рассчитать константу равновесия, если начальная концентрация кислоты равна 0,05 моль/л, а концентрация лактат-ионов в состоянии равновесия составляет 0,003 моль/л.

3. Для реакции:

H₃PO₄ + аденозин ⇄ АМФ + H₂O

стандартная энергия Гиббса (ΔG⁰) составляет 14 кДж/моль.

Рассчитать константу равновесия этой реакции и сделать вывод о практической обратимости этой реакции при 25⁰С. Определить степень превращения аденозина.

Вариант №12

1. Реакция протекает по уравнению: A + 2B ⇄ 3C. Начальные концентрации веществ A и B составляли соответственно 8 и 12 моль/л. На момент наступления химического равновесия в реакцию вступило 60% A. Определить:

1) величину константы равновесия;

2) является ли при данных условиях реакция практически обратимой (или необратимой);

3) направление смещения равновесия при данных условиях.

2. Константа равновесия процесса изомеризации:

3-фосфоглицерат ⇄ 2-фосфоглицерат

при 20⁰С равна 0,1558. Определить равновесный состав системы, если начальная концентрация 3-фосфоглицерата составляет 0,15 моль/л.

3. Для реакции гидролиза АТФ, протекающего по уравнению:

АТФ + H₂O ⇄ АДФ + Фосфат,

при 37⁰С константа равновесия равна 2,3·10⁵.

Определить направление протекания процесса в мышечной клетке, находящейся в состоянии покоя, если концентрации АТФ, АДФ и фосфата равны соответственно 5; 0,5 и 5 ммоль/л, а вода присутствует в значительном избытке.

Вариант №13

1. В состоянии химического равновесия в системе: A + 3B ⇄ 2C концентрации веществ составили: [A] = 0,1 моль/л; [B] = 0,4 моль/л; [С] = 1,6 моль/л. Определить:

1) величину константы равновесия;

2) является ли при данных условиях реакция практически обратимой (или необратимой);

3) направление смещения равновесия при данных условиях;

4) исходные концентрации веществ A и B.

2. Константа равновесия реакции:

глутамат + оксалоацетат ⇄ кетоглутарат + аспартат

при 25⁰С равна 7. Найти соотношение аспартат/глутамат, если равновесные концентрации оксалоацетата и кетоглутарата равны соответственно 10^-4 и 10^-3 моль/л.

3. Стандартная энергия Гиббса (ΔG⁰) для процесса изомеризации:

дигидроксиацетонфосфат ⇄ глицеральдегид-3-фосфат

составляет 7,5 кДж/моль.

Рассчитать константу равновесия этой реакции и сделать вывод о практической обратимости этой реакции при 25⁰С. Определить степень превращения дигидроксиацетонфосфата.

Вариант №14

1. В состоянии химического равновесия в системе: A + B ⇄ 2C концентрации веществ составили: [A] = 0,5 моль/л; [B] = 0,4 моль/л; [С] = 0,08 моль/л. Определить:

1) величину константы равновесия;

2) является ли при данных условиях реакция практически обратимой (или необратимой);

3) направление смещения равновесия при данных условиях;

4) исходные концентрации веществ A и B.

2. Константа равновесия реакции:

2-фосфоглицерат ⇄ фосфоенолпируват + H₂O,

протекающей при избытке воды, равна 0,5. Найти равновесные концентрации веществ, если начальная концентрация 2-фосфоглицерата равна 0,05 моль/л.

3. Для реакции:

пируват + аспартат ⇄ аланин + оксалоацетат,

при 30⁰С константа равновесия равна 0,22.

В цитоплазме некоторых клеток компоненты содержатся в следующих концентрациях: С(пируват) = С(аспартат) = 10^-2 моль/л; С(аланин) = 10^-4 моль/л; С(аспартат) = 10^-5 моль/л. Определить направление самопроизвольного протекания процесса при 30⁰С.

Вариант №15

1. Ядовитый газ фосген образуется по реакции:

CO + Cl₂ ⇄ COCl₂.

Начальные концентрации CO и Cl₂ составили 2 моль/л. При определённых условиях равновесие установилось, когда в реакцию вступило 80% CO. Определить:

1) величину константы равновесия;

2) является ли при данных условиях реакция практически обратимой (или необратимой);

3) направление смещения равновесия при данных условиях.

2. На момент наступления равновесия в системе:

фумарат + H₂O ⇄ малат

концентрация фумарата снизилась от 0,5 до 0,4 моль/л. Найти константу равновесия, считая концентрацию воды постоянной.

3. Для процесса:

АДФ + фосфат ⇄ АТФ + H₂O,

протекающего при избытке воды, ΔG⁰ = 31 кДж/моль. В мышце лягушки rectus abdominis концентрации АДФ, АТФ и фосфата составляют соответственно 1,25; 0,5 и 2,5 ммоль/л. Определить направление протекания процесса при 25⁰C.

Глава 4

РАСТВОРЫ

Растворы - это гомогенные системы переменного состава, состоящие из двух и более веществ, называемых компонентами. По агрегатному состоянию растворы могут быть газообразными (воздух), жидкими (кровь, лимфа) и твёрдыми (сплавы). В медицине наибольшее значение имеют жидкие растворы, которые играют исключительную роль в жизнедеятельности живых организмов. С образованием растворов связаны процессы усвоения пищи и выведения из организма продуктов жизнедеятельности. В форме растворов вводится большое количество лекарственных препаратов.

Для качественного и количественного описания жидких растворов используются термины «растворитель» и «растворённое вещество», хотя в некоторых случаях такое разделение является достаточно условным. Так, медицинский спирт (96% раствор этанола в воде) скорее следует рассматривать как раствор воды в спирте. Все растворители делятся на неорганические и органические. Важнейшим неорганическим растворителем (а в случае биологических систем – единственным) является вода. Это обусловлено такими свойствами воды, как полярность, низкая вязкость, склонность молекул к ассоциации, относительно высокие температуры кипения и плавления. Растворители органической природы разделяют на полярные (спирты, альдегиды, кетоны, кислоты) и неполярные (гексан, бензол, четыреххлористый углерод).

Процесс растворения в равной степени зависит как от природы растворителя, так и от свойств растворённого вещества. Очевидно, что способность образовывать растворы выражена у разных веществ по-разному. Одни вещества могут смешиваться друг с другом в любых количествах (вода и этанол), другие – в ограниченных (вода и фенол). Однако, следует помнить: абсолютно нерастворимых веществ не существует!

Склонность вещества растворяться в том или ином растворителе можно гипотетически определить, используя простое эмпирическое правило: подобное растворяется в подобном. Действительно, вещества с ионным (соли, щёлочи) или полярным (спирты, альдегиды) типом связи хорошо растворимы в полярных растворителях, например, в воде. И наоборот, растворимость кислорода в бензоле на порядок выше чем в воде, так как молекулы O₂ и C₆H₆ неполярны.

Степень сродства соединения к определённому типу растворителя можно оценить, анализируя природу и количественное соотношение входящих в его состав функциональных групп, среди которых выделяют гидрофильные (притягивающие воду) и гидрофобные (отталкивающие воду). К гидрофильным относят полярные группы, такие как гидроксильная (-OH), карбоксильная (-COOH), тиольная (-SH), амино (-NH₂). Гидрофобными считают неполярные группы: углеводородные радикалы алифатического (-CH₃, -C₂H₅) и ароматического (-C₆H₅) рядов. Соединения, имеющие в своем составе как гидрофильные, так и гидрофобные группы, называют дифильными. К таким соединениям относят аминокислоты, белки, нуклеиновые кислоты.

Теории растворов

В настоящее время признаны две основные теории растворов: физическая и химическая.