Изменение энтальпии системы в результате реакции не зависит от пути протекания реакции, а зависит только от начального и конечного состояния системы.

Закон Гесса позволяет складывать и вычитать термохимические уравнения (уравнение реакции вместе с тепловым эффектом). Важно, что он позволяет рассчитывать тепловые эффекты реакций, не проводя их!

Обычно все изменения энтальпии рассматривают при условии, что в начале и в конце процесса система находится при стандартных давлении и температуре. Рассматриваемое вещество берётся в количестве 1 моль. Тогда говорят о стандартных энтальпиях.

ПРИМЕР. Поясним идею закона Гесса.

Сожжём один моль углерода в кислороде до углекислого газа:

C(графит) + O₂(г) = CO₂(г); DH⁰_p = -393,5 кДж.

А теперь проведём эту реакцию в две стадии - сначала окислим углерод в угарный газ:

C(графит) + 1/2O₂(г) = CO(г); DH⁰_p1 = -110,5 кДж,

а потом окислим угарный газ в углекислый:

CO(г) + 1/2O₂(г) = CO₂(г); DH⁰_p2 = -283,0 кДж.

Коэффициент 1/2 здесь не означает дробного числа молекул. Его, как и все коэффициенты в термохимических уравнениях, следует считать равным числу молей. Указывается также агрегатное состояние вещества, а для твёрдых - тип структуры (аллотропная или полиморфная модификация).

Итак, видно, что при разбиении реакции на стадии её суммарный тепловой эффект не изменяется:

DH_p = DH_p1 + DH_p2.

В такой форме закон и был сформулирован Гессом.

Чтобы применять закон Гесса, для химических веществ вводят следующие ниже стандартные характеристики.

Стандартной энтальпией образования вещества DH⁰_f называется изменение энтальпии в процессе получения одного моля вещества из простых веществ. Для простых веществ полагается DH⁰_f = 0. Если один элемент образует несколько простых веществ, выбирают наиболее доступное и устойчивое в стандартных условиях (углерод - в форме графита, а не алмаза, кислород - в форме O₂, а не озона O₃).

Прочные сложные вещества обычно имеют сильно отрицательную энтальпию образования (вода, кварц, оксид алюминия Al₂O₃, оксид циркония ZrO₂, фторид кальция CaF₂). Они легко образуются из простых веществ, процесс идёт с выделением тепла. У непрочных веществ DH⁰_f>0 (оксиды золота Au₂O, Au₂O₃). Их нельзя получить прямой реакцией простых веществ.

Обычно пользуются следствиями из закона Гесса:

1) в результате кругового процесса (когда система в конце возвращается в исходное состояние) энтальпия не изменяется:DH =0;

2) изменение энтальпии в ходе обратной реакции противоположно её изменению в ходе прямой реакции: DH= -DH®;

3) изменение энтальпии в ходе реакции равно сумме энтальпий образования продуктов реакции минус сумма энтальпий образования исходных веществ:DH⁰_{реакции}= SDH⁰_{f,продуктов}-SDH⁰_{f,исходных веществ};

Стандартной энтальпией атомизации вещества DH⁰_a называется изменение энтальпии в процессе полного разрыва всех химических связей в одном моле вещества с образованием газа из нейтральных невзаимодействующих атомов. Другими словами, это - энтальпия образования одноатомных газов. Если известны DH⁰_a простых веществ, то для сложных они могут быть рассчитаны по энтальпиям образования. Обычно DH⁰_a простых веществ выражают на 1 моль атомов.

У инертных газов DH⁰_a=0, у остальных веществ эта величина положительна. Чем больше DH⁰_a, тем прочнее связи в веществе (графит, корунд).

Аналогично энтальпии, могут быть найдены изменения в ходе реакций и других функций состояния, например, энтропии.

Следует, однако, помнить, что, согласно третьему началу термодинамики, энтропии простых веществ в стандартных условиях не равны нулю.

Энтальпии реакций, в том числе, образования или атомизации, могут быть найдены экспериментально. Для этого реакции проводят в приборах, изолированных от окружающей среды. Тщательно измеряют изменение температуры, и, зная теплоёмкости реагентов и прибора, рассчитывают общий тепловой эффект. Теплоёмкости предварительно также определяют экспериментально.

Теплоёмкостьюназывают количество тепла, необходимое для нагревания предмета или некоторой массы вещества на один градус. Часто используют удельную теплоёмкость (вещество берётся в количестве 1 грамм или 1 килограмм) и молярную теплоёмкость (вещество берётся в количестве 1 моль). Например, для воды удельная теплоёмкость=4,18 Дж/(моль×К).

Энтальпии образования и атомизации используют для расчёта прочности химической связи.

ПРИМЕР.Рассчитаем энергию связи H-O в воде. Для этого нужно найти DH реакции:

H₂O (г) = 2 H (ат) + O (ат).

По следствию из закона Гесса получим:

DH_р= DH⁰_a(H₂O)= 2DH⁰_a(H) +DH⁰_a(O)-DH⁰_f(H₂O)

Стандартные энтальпии образования и атомизации равны:

H₂ + 1/2 O₂ = H₂O,

1/2 H₂ (г) = H (ат),

1/2 O₂ (г) = O (ат),

DH⁰_f(H₂O, г)= -241,8 кДж/моль;

DH⁰_a(H)= 218,0 кДж/моль;

DH⁰_a(O)= 249,2 кДж/моль.

Подставим числа:

DH_р= 436,0+249,2+241,8= 927,0 кДж/моль.

Атомизация газообразной воды представляет собой разрыв двух связей H-O. Поэтому энергия одного моля связей составляет 927,0/2 = 463,5 кДж/моль, а энергия одной связи получается делением на число Авогадро: 463,5×10⁺³ Дж/моль / 6,02×10⁺²³ моль^–1 = 7,7×10^–19 Дж.

Пользуясь термохимическими данными, можно сказать, насколько точно выполняется в химических реакциях закон сохранения массы. Связь между массой и энергией даёт уравнение Эйнштейна:

E = m×c²,

где c - скорость света (3×10⁺⁸ м/с).

Для химических реакций перепишем его в виде:

DH= Dm×c²;

Величина Dm называется дефектом массы. Для рассмотренной выше реакции сгорания 1 моля водорода (2 г) в кислороде (его полмоля составят 16 г) с получением 1 моля воды (18 г):

Dm = -241,8×10⁺³ Дж / 9×10⁺¹⁶ (м/с)² = -2,69×10^–12 кг

или -2,69×10^–12 кг / 0,018 кг × 100% = -1,49×10^–10 %.

Это столь ничтожное изменение массы, что его нельзя измерить никакими весами. Так как тепловые эффекты других химических реакций того же порядка, дефектом массы мы пренебрегаем и делаем вывод: масса продуктов химической реакции равна массе исходных веществ. Это и есть закон сохранения массы.

В ядерных реакциях дефект массы в тысячи раз больше, но тоже весьма мал.

5. ХИМИЧЕСКАЯ КИНЕТИКА

Химическая кинетика - это учение о скорости и механизме химических реакций.

Её интересует, как быстро расходуются исходные вещества и возникают продукты реакции, по какому пути идёт реакция, то есть к какому конечному продукту через какие промежуточные.

Это похоже на автобус или поезд - нас интересуют дорога, промежуточные станции, скорость движения, конечный пункт.

Скоростью химической реакции (СХР) называют изменение количества продукта реакции в единицу времени:

v=Dn_прод/Dt.

Размерность v при этом: [v]=моль/с. Можно контролировать СХР и по исходным веществам. Тогда: v=-Dn_исх/Dt, так как скорость должна быть величиной положительной, а исходные вещества расходуются, то есть Dn<0.

Часто рассматривают реакции, идущие в особых условиях:

1) в однородной, иначе говоря, в гомогенной среде (газовая смесь, раствор); в этом случае определяют объёмную СХР как изменение молярной объёмной концентрации вещества в единицу времени:

v _гом.= 1/V×Dn_прод/Dt = DC_прод/Dt (при V=const);

здесь V - объём реакционной смеси, C - молярная концентрация, то есть число молей вещества в единице объёма; обычные единицы измерения C: моль/л, моль/м³; а размерность СХР: [v _гом.]=моль/(л×с);

гомогенные реакции могут проходить быстро, так как в газе и жидкости легко происходит взаимное перемещение частиц - за доли секунды проходят реакции обмена в растворах или взрыв смеси водорода и кислорода;

2) на границе раздела фаз (гетерогенные реакции); одна из фаз может быть жидкостью или газом, другая обычно твёрдая;

в гетерогенных реакциях перемещение реагентов и продуктов реакции затрудняется и они обычно идут медленно - взаимодействие силикатных горных пород с водой может длиться тысячелетиями.

Скорость химических реакций зависит:

1) от природы реагентов; в химическом строении реагентов основным фактором является энергия разрыва наименее прочных связей, а также энергия удаления или присоединения электронов;

2) от концентрации исходных веществ; может влиять также содержание продуктов реакции; с повышением концентрации СХР обычно возрастает, ведь частицы реагентов чаще сталкиваются; для реакций с участием газов концентрация пропорциональна давлению: C=n/V=p/(R×T), поэтому СХР зависит и от давления;

3) от температуры; с повышением температуры скорость большинства реакций резко возрастает, так как быстро увеличивается число частиц с высокой энергией столкновения;

4) от скорости подвода реагентов и отвода продуктов на границе фаз гетерогенной реакции; в стационарных состояниях гетерогенные реакции обычно идут медленно, а измельчение и перемешивание сильно их ускоряет; порошки реагируют быстро, а крупные куски и монокристаллы - долго;

5) от присутствия в системе некоторых нерасходуемых веществ; они могут замедлять реакцию - это ингибиторы, и ускорять реакцию - катализаторы.

Химические реакции обычно идут во много стадий.

Рассмотрим пока простейший случай: представим, что гомогенная реакция вообще идёт всего в одну стадию, например, по схеме:

X + Y ® Z

(буквы здесь условно отражают три разных вещества). В этом случае выполняется закон действия масс (ЗДМ):

при постоянной температуре скорость одностадийной гомогенной химической реакции пропорциональна концентрации каждого из реагентов:

v = k×C_x×C_y.

Величина k называется константой скорости. Она равна скорости при единичных концентрациях. k зависит от температуры и природы реагентов и всех прочих факторов, кроме концентраций. Так как реакция гомогенная и размерность СХР моль/(л×с), то размерность k для рассмотренной реакции будет л/(моль×с).

ЗДМ объясняется тем, что для реакции между частицами они должны столкнуться. Число частиц, участвующих в одной стадии, называют молекулярностьюреакции.

Данная реакция является, как говорят, бимолекулярной (в элементарной стадии участвуют две частицы: одна - X и другая - Y). Молекулярность одностадийной реакции обычно равна 1 или 2, реже 3. Одновременное столкновение четырёх частиц совсем маловероятно.

Для тримолекулярной реакции

2X + Y ® Z, иначе говоря, X + X + Y ® Z,

закон действия масс выглядит так:

v = k×C_x×C_x×C_y = k×C_x²×C_y,

то есть коэффициент в уравнении реакции превращается в показатель степени в формуле для СХР.

ЗАДАЧА.Как изменится скорость одностадийной реакции 2X+Y ® Z, если концентрацию вещества X увеличить в 5 раз?

РЕШЕНИЕ. v_o=k×C_x²×C_y, v₁=k× (5×C_x)²×C_y=25×k×C_x²×C_y=25×v_o.

ОТВЕТ: увеличится в 25 раз.

Сложная реакция может протекать по последовательному (эстафетному) механизму, и с разветвлениями. С участием одних и тех же реагентов могут получаться разные продукты.

Сложные реакции и гетерогенные реакции не могут быть описаны моделью простых столкновений.

Сначала вещества 1 превращаются в вещества 2, потом вещества 2 - в вещества 3. Так, при окислении медного провода (Cu) кислородом воздуха сначала получается Cu₂O, а потом - CuO.

Вещества 1 одновременно превращаются и в вещества 2, и в вещества 3. Так, из сахара при брожении могут получиться: а) этиловый спирт, б) молочная кислота, в) уксусная кислота, г) ацетон и формальдегид.

В многостадийной реакции скорости "бегунов" в эстафете (стадий) могут различаться в миллионы раз. Как быстро дойдёт реакция до финиша, зависит в основном от самой медленной стадии; её называют лимитирующей. В ней могут участвовать не все исходные вещества и произвольные промежуточные продукты.

Поэтому зависимость общей скорости от концентрации исходных веществ (реагентов) может и не подчиняться закону действия масс. Однако лимитирующие стадии часто связаны с ослаблением связи именно в исходных веществах, а не в малопрочных промежуточных продуктах. Поэтому и для многостадийных реакций скорость обычно всё же увеличивается с ростом концентрации исходных веществ.

Запишем реакцию в произвольном виде:

aA + bB + ... ® xX + yY + ...

Для неё может выполняться так называемый кинетический или обобщённый закон действия масс:

v = k×C_A^a×C_B^b×...

В отличие от простой одностадийной реакции, a и b не обязательно равны a и b соответственно, а могут быть любыми числами, в том числе дробными и отрицательными. Величина p=a+b+... называется порядком сложной реакции. Она соответствует молекулярности простой реакции.

Например, взаимодействие тиосульфата натрия Na₂S₂O₃ c серной кислотой с образованием серы проходит в очень много стадий. Суммарное уравнение выглядит примерно так:

Na₂S₂O₃+H₂SO₄ ® Na₂SO₄ + S + H₂SO₃

S₂O₃^2– + H⁺ ® S + HSO₃^–

Хотя это уравнение и не отражает сложности процесса, мы можем ясно наблюдать, что при повышении концентрации тиосульфата скорость реакции возрастает.

Обратимся к температурной зависимости СХР.

С повышением температуры число столкновений частиц увеличивается (примерно на 1% на каждые 10 градусов). Однако обычно СХР растёт значительно быстрее.

Для многих реакций действует правило Вант-Гоффа-

с повышением температуры на каждые 10 градусов скорости многих химических реакций увеличиваются в 2-4 раза:

v₂/v₁ = g ^(t2–t1)/10.

Число g называют температурным коэффициентом реакции Вант-Гоффа.

ЗАДАЧА.Как изменится скорость реакции, если систему с коэффициентом Вант-Гоффа 3 нагреть от 20 до 60 °C?

РЕШЕНИЕ. v₂/v₁ = 3^(60–20)/10 = 3⁴ =81.

ОТВЕТ: увеличится в 81 раз.

Для объяснения также используются модели столкновений в гомогенной среде.

Считается, что частицы реагируют не при всяком столкновении, а только если энергия столкновения достаточна, чтобы преодолеть некоторый барьер, величина которого обычно в районе 30-200 кДж/моль. Его называют энергией активации Е_акт. Необходимо ослабить старые химические связи, образовать новые, а потом полностью разорвать ненужные. Промежуточное, частично разрушенное состояние веществ называют активным комплексом.

Типичная энергия активации в десятки раз ниже энтальпии атомизации реагентов и даже часто заметно ниже энергии отдельной связи. Это указывает на сохранение при активации большинства связей.

Эти представления приводят к следующему уравнению для температурной зависимости константы скорости реакции:

k = A×e-Е_акт/(R×T)или k = ln A - .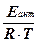

где е=2,718... - основание натуральных логарифмов, R - газовая постоянная, A - константа, не зависящая от T. Его называют уравнением Аррениуса.

Вблизи комнатной температуры коэффициенту Вант-Гоффа 2 отвечает типичная энергия активации в 50 кДж/моль.

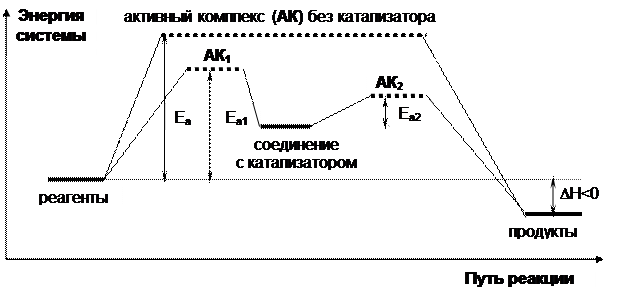Влияние катализатора сводится к снижению энергии активации. Катализатор образует нестойкие соединения с реагентами и изменяет природу лимитирующей стадии. На энергетической диаграмме показан гомогенный катализ (реакция в газе или растворе). Процесс разбивается на 2 стадии, с энергиями активации E_a1 и E_a2 и активными комплексами АК₁ и АК₂. В случае ингибитора АК₂ лежит выше по энергии, чем АК.

6. ХИМИЧЕСКОЕ РАВНОВЕСИЕ

В химии принято считать, что любой процесс может идти не только в прямом, но и в обратном направлении, иначе говоря, обратим.

Например, при 300-400^оС известь (оксид кальция) быстро реагирует с углекислым газом. Образуется карбонат кальция. Если, наоборот, карбонат кальция (известняк) прокалить при 1000^оС, он разложится на известь и углекислый газ. При температуре около 900^ОС в закрытой системе прямой и обратный процесс идут одновременно и примерно с одинаковой скоростью. Сосуществуют продукты реакции и исходные вещества.

В уравнениях реакций обратимость показывают двумя стрелками вместо равенства:

CaCO₃ Û CaO + CO₂.

Система, в которой установились неизменные во времени концентрации реагентов и продуктов и выровнялись температура и давление, называется равновесной. В гетерогенной системе при этом ещё устанавливаются одинаковые концентрации компонентов в каждой фазе.

Равновесие принято описывать термодинамически и кинетически.

Сначала рассмотрим ещё одну важную функцию состояния - энергию Гиббса G. Она даётся определением:

G = H -T×S.

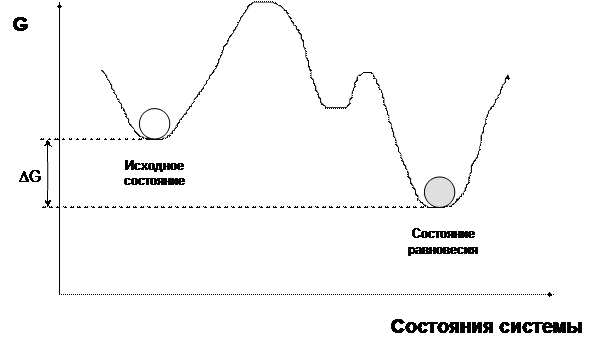
Если реакции проводятся при постоянном давлении и температуре, то самопроизвольно происходят процессы, которые сопровождаются уменьшением энергии Гиббса (DG<0). Точно так же мячик, лежащий на горке, самопроизвольно скатывается в долину или ямку. Процесс идёт до достижения самого глубокого минимума G.

Обычно записывают такое выражение для энергии Гиббса:

DG^o » DH^o-T×DS^o,

а в качестве DH^o и DS^o рассматривают изменение стандартных величин.

Это уравнение позволяет оценить возможность самопроизвольного протекания процесса при разных температурах (давление обычно считается атмосферным). Возможны 4 варианта:

- DH^o<0, DS^o>0; тогда DG^o<0 при любых T;

- DH^o<0, DS^o<0; тогда DG^o<0 при низких T (пренебрегаем вторым слагаемым);

- DH^o>0, DS^o>0; тогда DG^o<0 при высоких T (пренебрегаем первым слагаемым );

-

DH^o>0, DS^o<0; тогда при любых T будет DG^o>0.

Пользуясь следствием из закона Гесса, рассчитаем DH^o и DS^o реакции разложения известняка.

Вещество	DH0 образования, кДж/моль	DS0 образования, кДж/(моль×К)
CaCO3	-1207,0	0,0887
CaO	-635,5	0,0397
CO2	-293,5	0,2137

По этим данным получаем DH^o разложения = +178,0 кДж/моль, DS^o разложения = +0,1647 кДж/(моль×К). Поэтому ожидается, что реакция возможна только при высоких температурах.

Действительно, при 25^ОС (298 K) DG^o=+128,92 кДж/моль, а при 1000^ОС (1273 К) DG^o= 31,66 кДж/моль.

Вернёмся к описанию равновесия.

Итак, с точки зрения термодинамики, при постоянном давлении и температуре равновесию отвечает минимум энергии Гиббса.

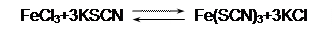В кинетике считают, что в состоянии равновесия выравниваются скорости прямой и обратной реакций.

Рассмотрим реакцию обмена в водном растворе:

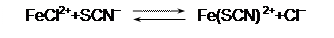В сокращённом ионном виде она выглядит так:

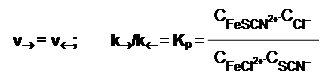Ион Fe(SCN)²⁺ имеет интенсивный красный цвету, остальные вещества бесцветны.

По закону действия масс, скорость для прямой реакции: v_® = k_®×CFeCl²⁺×CSCN^-; для обратной - v = k×CFeSCN²⁺×CCl^-.

При равновесии:

Величина K_p называется константой равновесия реакции. Она выражает соотношение между равновесными концентрациями продуктов реакции (произведение в числителе) и исходных веществ (произведение в знаменателе).

Для газообразных веществ принято концентрации заменять парциальным давлением. Это родственные величины. Из уравнений p×V=n×R×T и C=n/V получаем С=p/(R×T)иp=C×R×T.

Для гетерогенных реакций в константу равновесия, как и в закон действия масс, входят только концентрации веществ, находящихся в жидкой фазе, или парциальные давления веществ, находящихся в газообразной фазе. Поэтому, например, над известняком при каждой температуре своё вполне определённое давление CO₂:

CaCO₃¯ ® CaO¯ + CO₂­.

K_p=pCO₂.

Мы подробно изучим несколько разновидностей констант равновесия в теме "Растворы".

Константа равновесия, как и константа скорости, не зависит от концентраций, но зависит от температуры. Катализаторы на константу равновесия не влияют, однако они ускоряют достижение равновесия.

Существует связь между константой равновесия реакции при данных давлении и температуре и стандартным изменением в ходе неё энергии Гиббса:

K_p = e-DG^o/(R×T)или lnK_p = -DG⁰/(R×T).

Если K_p>>1, то в равновесной смеси сильно преобладают продукты реакции, исходных веществ практически не остаётся, а DG^o<0. Если K_p<<1, то DG^o>0 и реакция практически не идёт (в равновесной смеси сильно преобладают исходные вещества).

В теории равновесий важнейшее место занимает принцип Ле-Шателье: если на систему, находящуюся в равновесии, оказывается внешнее воздействие, в ней усиливается процесс, ослабляющий это воздействие.

Например, при нагревании усиливается эндотермическая реакция и в новом равновесии будет больше продуктов этой реакции. При охлаждении, напротив, усиливается эндотермическая реакция. Например, бурый газ NO₂ превращается в бесцветный газ N₂O₄ c выделением тепла. Около 0^ОС в равновесной смеси преобладает N₂O₄, а около 100^ОС -NO₂.

2NO₂ Û N₂O₄; K_p=pN₂O₄/(pNO₂)²

По значениям DG^o реакции разложения известняка при разных температурах оценим константы равновесия. При 25^oС DG^o=+128,92 кДж/моль и К_р=2,528×10^–23. При 1000^oС DG^o=31,66 кДж/моль и К_р=19,92. Для этой реакции К_р отвечает давлению углекислого газа в атмосферах.

Реакции с участием газов обычно весьма чувствительны к давлению. При повышении давления, по принципу Ле-Шателье, усиливается реакция, идущая со снижением объёма и наоборот. Рассмотренная реакция с оксидами азота приводит к уменьшению объёма (из двух молей исходного газа получается 1 моль газа-продукта), поэтому при повышении давления в равновесной смеси становится больше N₂O₄.

При увеличении концентрации одного из веществ усиливается реакция, в которой это вещество расходуется. Если это исходное вещество, то усиливается прямая реакция, и в новом равновесии становится больше продуктов реакции. Так влияет на приведённое равновесие с солями железа добавка в систему FeCl₃ или KSCN. Если добавить продукт реакции (KCl, точнее, Cl^-), усилится обратная реакция, в результате чего окраска ослабевает (расходуется Fe(SCN)²⁺).

Количество фаз, которые могут находиться в равновесии, ограничено, что выражается правилом фаз Гиббса:

С+Ф = К+П.

Здесь Ф - число фаз, К - число компонентов, П - число параметров состояния, определяющих равновесие (обычно, это - температура и давление, П=2), С - число степеней свободы (число параметров, которые могут изменяться без изменения числа фаз, С³0).

На представленной диаграмме состояния воды (К=1, П=2) есть такие объекты:

двумерные области (С=2), где в равновесии находится одна фаза (поля льда, жидкой воды и пара);

линии (С=1), где в равновесии находятся 2 фазы (линии плавления льда, кипения воды и испарения льда);

тройная точка (С=0), где в равновесии находятся 3 фазы;

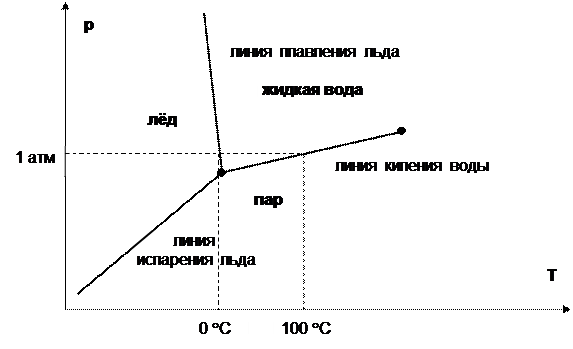
критическая точка (ею справа обрывается линия кипения); в этой точке исчезает различие между жидкостью и паром.

На диаграмме состояния углерода C есть поля графита, алмаза, жидкого и газообразного углерода.

Диаграмма кремнезёма SiO₂ включает поля кварца, тридимита, кристобалита, коэсита, стишовита, а также жидкости и пара.

Такие модификации, как алмаз или стишовит являются темодинамически стабильными только в области высоких температур и/или давлений. Но их удаётся сохранить и вблизи стандартных условий, если быстро снизить температуру и давление. В исторической геологии, пользуясь полиморфизмом, устанавливают температуру и давление в момент формирования горной породы.

строение вещества

7. ОСНОВЫ КВАНТОВОЙ МЕХАНИКИ

Атомы, молекулы и составляющие их частицы настолько малы, что для них не годятся законы природы, привычные для больших объектов. Устройство и саму устойчивость атомов объясняет квантовая механика. Её исходные положения таковы:

- все микрообъекты обладают свойствами и частицы, и волны; так, световым волнам отвечают частицы (фотоны), а электроны, протоны и нейтроны проявляют волновые свойства; длина волны микрообъекта lподчиняется уравнению де Бройля:

l=h/(m×v);

- здесь m - масса, v - скорость, h - постоянная Планка; h=6,626×10^–34 Дж×с;

- любая физическая величина, описывающая микрообъект, изменяется небольшими неделимыми порциями - квантами; в частности, квантуются величины энергииE,механического момента J,магнитного момента M_J; иначе говоря, они имеют дискретные значения, т.е. отдельные, отстоящие друг от друга;

механический момент J = m×v×r характеризует вращение частицы вокруг некоторого центра (с расстоянием r от него); при движении заряженных частиц возникает электрический ток, что характеризуется магнитным моментом M_J = I×S(I - сила тока, S - площадь контура с током);

- в каждом состоянии микрообъект обладает определёнными значениями E, J, M_J и другими измеримыми (наблюдаемыми) физическими величинами; среди состояний микрообъекта есть одно, обладающее наименьшей энергией - основное состояние; остальные состояния системы называются возбуждёнными; при переходе в более высокое по энергии состояние квант энергии (фотон) поглощается, а при переходе в состояние с меньшей энергией - излучается; энергия кванта определяется уравнением Планка:

E=h×f;

где f=с/l - частота кванта, с=2,998×10⁸ м/с - скорость света.

По формулам E=h×f и l=c/f можно вычислить длины поглощаемых или излучаемых волн. Видимой части спектра соответствуют:

Энергия перехода, эВ	Длина волны, нм	Цвет
1,65-1,91	750-650	красный
2,95-3,10	420-400	фиолетовый

Энергии 1эВ на частицу соответствует 96485 кДж/моль.

Состояние квантовой системы полностью описывается так называемой волновой функцией Y (пси). В случае атома водорода интеграл |Y|² по некоторому объему V равен вероятности встретить электрон в этом объёме.

Y можно найти решением волнового уравнения Дирака или Шрёдингера.

Сами эти достаточно сложные уравнения мы записывать и решать не будем.

В СЛУЧАЕ АТОМА ВОЛНОВОЕ УРАВНЕНИЕ ИМЕЕТ РЕШЕНИЕ ТОЛЬКО ПРИ ОПРЕДЕЛЁННЫХ (дискретных) ЗНАЧЕНИЯХ ЭНЕРГИИ, т.е. ЭНЕРГИЯ АТОМА КВАНТУЕТСЯ.

Вот почему спектры атомов - линейчатые (состоят из отдельных линий). Например, атом водорода может иметь значения энергии:

E_n = -13,6/n² эВ,

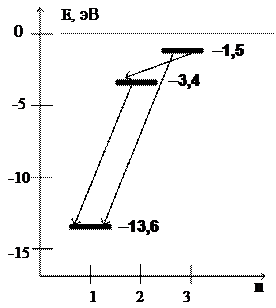где n - целое положительное число, называемое главным квантовым числом. n определяет не только энергию, но и размер атома.

Как видно, энергии атомов имеют отрицательные значения, т.к. за ноль принята энергия свободных электронов и ядер. n=1 соответствует наиболее низкая энергия, то есть, это - основное состояние H.

В случае атома водорода особенно просто разделяют механический момент Jна орбитальный момент (отвечает движению электрона вокруг ядра) L и собственный (он же - спиновый) момент S (условно отвечает вращению электрона вокруг своей оси). L и S квантуются и складываются как векторы, давая полный момент J.

Названным величинам отвечают новые квантовые числа:

- орбитальное l (орбитальный механический момент), целые числа, 0 £ l <n;

- магнитное m_l (его ориентация в пространстве), целые числа, - l £ m_l £ l;

- спиновое s (собственный механический момент), s=1/2;

- магнитное спиновое m_s (его ориентация в пространстве), -1/2 или 1/2.

Для водорода состояние атома определяется его единственным электроном. Поэтому квантовые числа ПРИПИСЫВАЮТ не атому в целом, а электрону.

Обычно состояние электрона в атоме характеризуют тройкой квантовых чисел (n,l,m_l). Это называется орбиталью. Говорят, что на орбитали располагается электрон со значением спина (точнее, m_s) -1/2 или 1/2. Каждой орбитали соответствует своё значение энергии и своя волновая функция Y.

Энергия атома водорода зависит только от n. Совокупность состояний с одинаковым значениемn называютэнергетическим уровнем.

Совокупность состояний одного уровня с одинаковым значениемl называют энергетическим подуровнем. Подуровни обозначают буквами:

l
обозначение	s	p	d	f
ml	0	-1, 0, 1	-2, -1, 0, 1, 2	-3, -2, -1, 0, 1, 2, 3
число орбиталей

Орбитали можно изображать графически. Формой орбитали обычно называют поверхность, внутри которой электрон находится с вероятностью 95%. s-орбиталь имеет сферическую форму, p-орбиталь - гантелеообразную, d-орбиталь - четырёхлепестковую форму или форму гантели с колечком.

8. МНОГОЭЛЕКТРОННЫЕ АТОМЫ

Гораздо более сложную систему, чем атом водорода, представляют собой многоэлектронные атомы. В них, кроме взаимодействия ядра и электронов, есть и межэлектронное взаимодействие. Усложнение атома проявляется, например, в значительном увеличении количества спектральных линий, которое зависит от числа квантовых состояний атома.

Волновое уравнение в случае многоэлектронного атома тоже усложняется и для него могут быть найдены только приближённые решения.

Обычно пользуются одноэлектронным (иначе - орбитальным) приближением. Считают, что состояние атома складывается из состояний отдельных электронов, а каждый из них характеризуют таким же набором квантовых чисел, что и электрон в атоме водорода. Затем говорят только о состояниях отдельных электронов - их волновых функциях, энергиях, орбитальных и собственных моментах.

Мы тоже ограничимся орбитальным приближением.

Для многоэлектронных атомов выполняется принцип Паули: в атоме не может быть двух электронов с одинаковым набором квантовых чисел.

Иначе говоря, на одной орбитали может разместиться максимум 2 электрона, но с противоположными ориентациями спина, т.е. со значениями m_s 1/2 и -1/2. При этом электроны называют спаренными. Обычно орбиталь обозначают квантовой ячейкой - клеткой или чертой, где стрелочкой показывают ориентацию спинов.

Легко понять, что s-подуровень может вместить до двух электронов, p-подуровень - до шести, d-подуровень - до 10, f-подуровень - до четырнадцати.

Энергия электрона в многоэлектронном атоме определяется не только значением n, но и значением других квантовых чисел, особенно - l. Именно поэтому выделяют не только энергетические уровни, но и подуровни - состояния с одинаковыми значениями n и l (и, вследствие этого, близкие по энергии).

Удобную схему порядка заполнения подуровней в нейтральных многоэлектронных атомах предложил Клечковский.

Согласно первому правилу Клечковского, подуровни заполняются в порядке увеличения суммы n+l (главного и орбитального квантовых чисел). Это отражает сильную зависимость энергии от обоих этих чисел.

Например, сначала заполняется 2s-подуровень (n+l=2), потом 2p-подуровень (n+l=3).

Согласно второму правилу Клечковского, в случае одинаковой суммы n+l, в первую очередь заполняются подуровни с минимальным n. Это означает, что энергия больше зависит от n, чем от l.

Например, подуровни с n+l = 5 заполняются в такой последовательности: 3d (n = 3, l = 2), 4p (n = 4, l = 1), 5s (n = 5, l = 0).

Заполнение электронами подуровня подчиняется правилу Хунда: из двух состояний выгоднее обладающее наибольшим суммарным спином (то есть, наибольшим числом неспаренных электронов).

ПРИМЕР. Рассмотрим электронное строение атома Fe. В нём содержится 26 электронов. Порядок заполнения подуровней:

n+l	1	2	3	3	4	4	5	5
подуровень	1s	2s	2p	3s	3p	4s	3d	4p
число электронов подуровня
общее число электронов

Последующие подуровни нам не потребуются. Видно, что последним заполняется 3d-подуровень. Поэтому железо называют 3d-элементом. Согласно правилу Хунда, сначала на каждой орбитали этого подуровня располагается по одному электрону, а потом добавляется ещё один, последний электрон в атоме. Таким образом, в атоме остаётся 4 неспаренных электрона, которые и вызывают магнитные свойства железа и его соединений.

Внешними электронами называют располагающиеся на орбиталях с наибольшими n и l. Эти электроны наиболее удалены от ядра, имеют максимальную энергию, иначе говоря, слабее остальных удерживаются атомом. Внешние электроны и орбитали, которые могут участвовать в образовании химической связи, называют валентными. Остальные электроны в атоме называют внутренними. Они при химических процессах затрагиваются слабо.

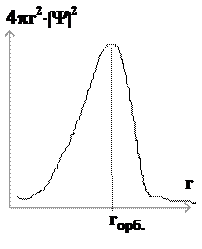
Размер атома - понятие нечёткое (атом не имеет границы). Часто для характеристики размера изолированного атома атома используют наиболее вероятное расстояние от ядра самого внешнего электрона - орбитальный радиус. Наибольший орбитальный радиус (2,52 Ă) - у атома цезия, а наименьший - у гелия (0,29 Ă).

С точки зрения химии важны такие свойства атома как: а) энергетический эффект удаления одного или нескольких электронов из атома; (энергия или потенциал ионизации); б) энергетический эффект присоединения одного дополнительного электрона к атому; (сродство к электрону).

Энергия (потенциал) ионизации атома находится интервале от 3,89 эВ (цезий) до 24,59 эВ (гелий). Видно, что крупный атом ионизировать легче.

Наибольшая энергия сродства к электрону - у хлора (3,62 эВ), а к некоторым атомам (азот, аргон, магний и др.) присоединение дополнительного электрона невыгодно. Обратите внимание: самая большая энергия сродства меньше самой малой энергии ионизации.

Возбуждённые состояния атома отличаются от основного распределением электронов по орбиталям. Например, возбуждённое состояние атома углерода с четырьмя неспаренными электронами выше основного (с двумя неспаренными электронами) на 4,18 эВ. Такого рода возбуждение может произойти под действием ультрафиолетового излучения или при влиянии других атомов.

9. ПЕРИОДИЧЕСКИЙ ЗАКОН

Последовательность заполненных подуровней атома с указанием числа электронов на них называют электронной конфигурацией.

С конфигурацией внешних подуровней атомов связано устройство Периодической системы Менделеева.

Рассмотрим внешние подуровни различных атомов:

Fe	4s2 3d6		C	2s2 2p2
F	2s2 2p5		Cl	3s2 3p5

Вы видите, что электронные конфигурации атомов хлора и фтора сходны. Это приводит и к сходству их химических свойств. Вы знаете, что эти элементы, а также бром и иод называют галогенами. У галогенов одинаковая конфигурация внешних заполненных подуровней ns²np⁵. В периодической системе их помещают в одну седьмую группу.

Также похожи по свойствам кислород, сера, селен и теллур, имеющие конфигурацию атомов ns²np⁴, или литий, натрий, калий, рубидий, цезий с конфигурацией ns¹.

Итак, при последовательном увеличении заряда ядра (то есть атомного номера) у нейтральных атомов периодически повторяется электронная конфигурация внешнего уровня, что приводит к сходству химических свойств.

Это - современная формулировка периодического закона.

В один период помещают элементы, атомы которых имеют одинаковое главное квантовое число n самых внешних электронов. Номер периода равен n.

В одну группу помещают элементы, атомы которых имеют одинаковое электронов на валентных подуровнях. Это число чаще всего равно номеру группы. Элементы, у которых в стадии заполнения электронами находятся только внешний уровень с квантовым числом n, формируют главную подгруппу. Если в стадии заполнения находятся также уровни с n-1 и/или n-2, элементы формируют побочную подгруппу.

Например, главную подгруппу 7 группы формируют галогены с конфигурацией ns²np⁵, а побочную подгруппу - Mn, Tc, Re с конфигурацией (n-1)d⁵ns².

Все свойства атомов (орбитальные радиусы, потенциалы ионизации, энергии сродства к электрону и другие) подчиняются Периодическому закону.

Энергии (или энтальпии) атомизации простых веществ также периодически зависят от атомного номера. Наименьшие, равные нулю стандартные энтальпии атомизации - у инертных газов. Наибольшие - у таких прочных металлов, как вольфрам (849,4 кДж/моль), тантал (782,0 кДж/моль) и других. Из неметаллов всех сильно превосходит углерод (716,7 кДж/моль).

Периодическую зависимость проявляют и многие свойства сложных веществ, например, энтальпии образования оксидов или галогенидов.

В Периодической таблице отличают s-, p-, d- и f-элементы - по орбитальному квантовому числу заполняющегося подуровня.

Выделяют также:

щелочные металлы (s-элементы 1-й группы - Li-Fr),

щелочноземельные металлы (s-элементы 2-й группы - Mg-Ra),

галогены (p-элементы 7-й группы - F-At),

халькогены (p-элементы 6-й группы - O-Po),

триаду железа (3d-элементы 8-й группы - Fe,Co,Ni),

платиновые металлы (4d- и 5d-элементы 8-й группы - Ru,Rh,Pd,Os,Ir,Pt),

редкоземельные металлы (4f-элементы, а также Sc и Y).

В геохимии элементы разделяют на атмофильные элементы (составляющие атмосферу - N, O, Ar и др.), литофильные (слагающие земную кору - Si, Al, Ca, Mg, Na и др.), сидерофильные (подобные железу, преобладающие в ядре Земли - Fe, Co, Ni и др.) и халькофильные (подобные меди, образующие устойчивые сульфидные руды - Cu, Mo, W и др.).

В первые два типа входят преимущественно элементы главных подгрупп, в остальные - преимущественно элементы побочных подгрупп.

10. ХИМИЧЕСКАЯ СВЯЗЬ

Сближение атомов сказывается на движении электронов в них или даже вызывает перераспределение электронов. Этому сопутствует выигрыш энергии, иными словами - образование связи между атомами.

Взаимодействие между атомами считается химической связью, если выигрыш энергии составляет более 1 эВ на атом (обычно: 3-5), иначе говоря - более 100 кДж на моль атомов.

Если же выигрыш энергии составляет 0,1 эВ и менее, взаимодействие называется остаточным (иначе - межмолекулярным, ван-дер-ваальсовым).

Напомню, что энергия, необходимая для превращения вещества в изолированные атомы называется энергией атомизации. Например, для разрыва всех химических связей в одном моле железа требуется 416,3 кДж или 4,31 эВ/атом.

Состояние внутренних электронов атомов в веществе очень похоже на их состояние в изолированных атомах. Однако внешние электроны атомов образуют в веществе совершенно новые молекулярные орбитали и энергетические уровни.

По характеру перераспределения электронов между атомами выделяют следующие типы химической связи:

КОВАЛЕНТНАЯ СВЯЗЬ - осуществляется общей для двух атомов парой электронов с противоположной ориентацией спинов; считается, что положительно заряженные атомные остатки притягиваются к общей области повышенной электронной плотности;

ИОННАЯ СВЯЗЬ - один или более электронов полностью переходят от одного атома к другому; при этом образуются ионы противоположного заряда, которые притягиваются друг к другу;

МЕТАЛЛИЧЕСКАЯ СВЯЗЬ - некоторая часть электронов атома поступает в общее пользование всеми атомами кристалла, иначе говоря - делокализуется; возникает притяжение между газом делокализованных электронов и положительными атомными остатками.

Как видно, все типы связи имеют электрическую природу. Когда атомы находятся один возле другого, их внешние электроны начинают чувствовать соседний атом.

Способность атома в веществе оттягивать на себя электроны называют электроотрицательностью (ЭО).

Можно определить ЭО по свойствам изолированных атомов, её приравнивают к полусумме потенциала ионизации и энергии сродства к электрону:

ЭО=(I₁+E_cр)/2.

В главных подгруппах Периодической системы ЭО сверху вниз уменьшается, а в периодах слева направо - увеличивается. Иначе говоря, рост ЭО означает усиление неметаллических свойств. Если исключить инертные газы и нестабильные элементы, наибольшая ЭО у F, O и Cl, наименьшая - у Cs, Rb, K, Ba.

В соединении тип связи можно предсказать по ЭО атомов.

Если ЭО сильно отличаются, связь будет ионной - например, в NaCl от атомов натрия электрон перейдёт к атомам хлора. Если ЭО близки и велики, связь будет ковалентной, например, в молекуле N₂. Если ЭО близки и малы, связь будет металлической, например, в кристалле натрия.

Почему электронам выгодно переходить от атома к атому? Потому что происходит выигрыш энергии за счёт образования стабильных электронных конфигураций. Чаще всего это восьмиэлектронная благородногазовая оболочка ns²np⁶ (октет). Такая оболочка у Na⁺ (2s²2p⁶) и Cl^–(3s²3p⁶). В октете распределение заряда имеет сферическую симметрию.

Стабильны также конфигурации nd¹⁰ и nd⁵.