Полярографическое исследование кинетики электродного процесса

ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

В полярографическом методе исследования в качестве рабочего используется электрод первого рода в виде растущей капли жидкого металла (обычно ртути), вытекающей из капилляра – капельный электрод. Он состоит из длинного узкого капилля­ра, на конце которого периодически образуются и отрываются небольшие капли металла (диаметром около 1–2 мм). Поляри­зация капли осуществляется относительно большого вспомогательного электрода обычно из того же металла на дне ячейки. Если площадь вспомогательного электрода много больше площади рабочего, то поляризацией вспомогательного электрода можно пренебречь и в простейшем случае отсчитывать потенциал рабочего электрода от потенциала вспомогательного, т.е. использовать его еще и как электрод сравнения (см. рис.1).

Однако в общем случае потенциал рабочего электрода измеряется по отношению к отдельному постоянному электроду сравнения (обычно это нормальный или насыщенный каломельный электрод) (рис. 3).

Рис.1. Схема простой полярографической цепи

1 – вспомогательный электрод, он же электрод сравнения; 2 – раствор электролита; 3 – рабочий капельный электрод. А – амперметр; V – высокоомный вольтметр; И – источник регулируемого напряжения – потенциостат. Площадь вспомогательного электрода намного больше площади рабочего электрода

Ток в цепи капельного электрода зависит от времени. Поэтому при измере­ниях ток усредняют по периоду капанья электрода.

К рабочему и вспомогательному электродам прикладывают напряжение, меняющееся во времени от начального до некоторого заданного значения по определенному (чаще всего линейному) закону, и измеряют силу тока в электролитической цепи, определяя одновременно изменение потенциала капельного электрода относительно электрода сравнения.

Разность потенциалов между капельным электродом и электродом сравнения определяется выражением

Δφ = φ_р.э – φ_э.с. + IR (1)

где φ_р.э – потенциал рабочего электрода; φ_э.с. – потенциал электрода сравнения, который принят равным нулю; I – сила тока в цепи рабочего и вспомогательного электродов; R – сопротивление электролита, между рабочим электродом и электродом сравнения; IR – омическое падение напряжения в электролите между рабочим электродом и электродом сравнения.

Величина IR вносит ошибку в измерение величины φ_р.э, для уменьшения которой снижают R, приближая носик электрода сравнения к рабочему электроду как можно ближе, как это показано на рис.3.

Потенциал капельного электрода смещается в отрицательную сторону от равновесного, на нем идет реакция восстановления и электрод является катодом, на вспомогательном электроде протекает реакция окисления и он является анодом. Через цепь протекает ток небольшой силы, и он лишь незначительно влияет на соотношение кон­центраций веществ в объеме. При этом потенциал вспомогательного электрода не изменяется.

Размер и соответственно площадь капли изменяются от нуля до некоторой величины, после чего капля отрывается и падает вниз на вспомогательный электрод. Так происходит идеальное обновление поверхности рабочего электрода, что обусловливает независимость тока на каплях от времени электролиза. Период капания составляет несколько секунд.

Любая электрохимическая реакция состоит из ряда последовательных стадий. Участники реакции должны доставляться к поверхности электродов – стадия массопереноса или диффузии, затем они могут претерпевать химическое превращение, переводящее их в более реакционноспособную форму –стадия предшествующей химической реакции. После этого происходит присоединение или освобождение одного или нескольких электронов (восстановление или окисление), которое может протекать в одну или несколько стадий - в целом это стадия разряда-ионизации или стадия переноса электрона. После собственно электрохимической стадии должно происходить удаление продуктов реакции.

При стационарном протекании электрохимической реакции скорости всех стадий одинаковы, но скорость суммарной реакции определяется скоростью самой медленной стадии, которая называется лимитирующей.

При замедленной стадии массопереноса реакция является обратимой, при замедленной стадии разряда-ионизации реакция является необратимой.

Ток в цепи полярографической установки между рабочим и вспомогательным электродами начинает течь, когда при изменении напряжения величина потенциала капельного электрода достигает потенциала начала разряда ионов, находящихся в растворе. Сначала с ростом отри­цательного потенциала электрода сила тока увеличивается, но при этом уменьшается концентра­ция электрохимически активного иона – деполяризатора у поверхности электрода, вследствие замедленности стадии подвода ионов деполяризатора из объема раствора к поверхности электрода конвективной диффузией. Когда концентрация уменьшается до нуля, ток достигает постоянной величины, кото­рая зависит от скорости переноса деполяризатора к поверхности электрода. Этот ток называется предельным диффузионным.

Полярографическую кривую, выражающую зависимость силы тока от потенциала капельного электрода называют полярографической волной.

Если в растворе присутствует еще другое вещество, которое может восстанавливаться в области потенциалов, достаточно отличаю­щихся от потенциалов образования первой волны, то при соответст­вующем потенциале наблюдается дальнейшее увеличение силы тока и форми­руется новая полярографическая волна (рис.2).

Высота полярографической волны, т.е. значение предельного диффузионного тока обычно пропорциональна концентрации восстанавливающегося вещества.

Если на капельном электроде протекает обратимая реакция

Ox + ne 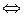Red (2)

где Ox и Red – окисленная и восстановленная формы вещества соответственно; n – число электронов, участвующих в реакции; е – элементарный заряд,

то согласно теории нестационарной диф­фузии, которая реализуется на таком электроде, выражение для плотности предельного диффузионного тока, полученное решением уравнения второго закона Фика, можно представить в виде

i_пр = nFD_Оx 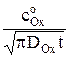(3

где F – число Фарадея, Кл/(моль эквивалентов); D_Оx – коэффициент диффузии деполяризатора – окисленной формы, м²/с; 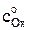– концентрация деполяриза­тора в объеме раствора, моль/м³; t – время поляризации при потенциале, соответствующем предельному диффузионному току, с.

Величина полного предельного диффузионного тока равна

I_пр = i_пр S = 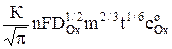, (4)

где S– площадь капли, зависящая от времени по уравнению: S = 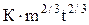, м²; m – скорость вытекания металла из капилляра, кг/с; К = ,

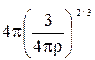r – плотность металла капельного электрода, кг/м³.

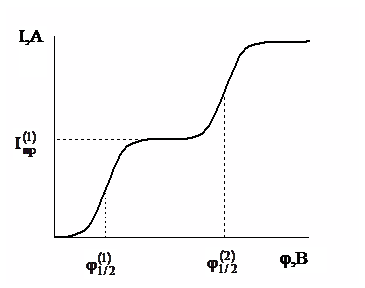Рис. 2. Схема полярограммы при наличии в растворе двух деполяризаторов (1) и (2)

Для ртутного капельного электрода среднюю за время t жизни капли величину предельного диффузионного тока представляют уравнением Д. Ильковича

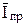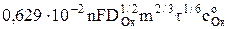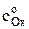= = A_Оx , (5)

где A_Оx= 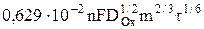– константа Ильковича для процесса восстановления.

На основании уравнения Ильковича установлено, что средний предельный диффузионный ток зависит от высоты h столба ртути в капилляре:

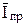~ h^1/2 , то есть с ростом высоты должна возрастать величина 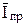. Наличие такой зависимости, полученной экспериментально, подтверждает диффузион­ный режим катодного процесса.

Предположим, что в начале опыта в растворе концентрация восстановленной формы 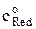равна нулю, присутствует только окисленная форма и её концентрация у поверхности электрода не равна нулю, т.е. предельный ток не достигнут, так как потенциал электрода положительнее потенциала, соответствующего предельному току. Тогда уравнение для среднего тока, протекающего через электрод, запишется в виде

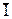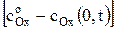= A_Оx , (6)

где с_Оx (0,t) – концентрация окисленной формы у поверхности электрода за пределами двойного электрического слоя в любой момент времени поляризации, моль/м³.

Используя уравнения (5) и (6) и уравнение Нернста для потенциала электрода можно получить выражение для обратимой полярографической волны.

В общем случае при протекании реакции (1) потенциал электрода равен

φ = φ^о + 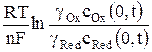, (7)

где g_Оx и g_Red – коэффициенты активности окисленной и восстановленной форм ионов; c_Red(0,t) – концентрация восстановленной формы у поверхности электрода за пределами двойного электрического слоя в любой момент времени поляризации.

Из уравнений (5) и (6) следует

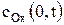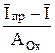= . (8)

Если вещества Ox и Red не адсорбируются на ртути, то в стационарном состоянии поток окисленной формы к поверхности электрода равен потоку восстановленной формы от поверхности ртути в раствор или в объем ртутной капли.

При условии 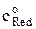= 0 поток восстановленной формы выражается уравнением

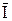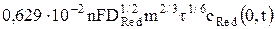= = A_Red 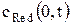, (9)

где A_Red = 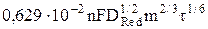– константа Ильковича для процесса окисления.

Подставляя выражения для поверхностных концентраций из (8) и (9) в уравнение Нернста, получим

φ = φ^о + 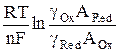+ 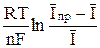(10)

или с учетом выражений для констант Ильковича, имеем

φ = φ^о + 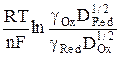+ 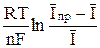= φ_1/2 + 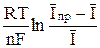. (11)

Полученная зависимость потенциала капельного электрода от средней величины тока является уравнением полярографической волны обратимой электродной реакции.

Величина φ_1/2 = φ^о + 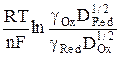называется потенциалом полуволны, так как φ = φ_1/2 при 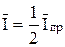. Потенциал полуволны в случае разбавленных растворов, когда можно считать коэффициенты активности постоянными, не зависит от концентрации деполяризатора, а определяется лишь природой окислительно-восстановительной системы.

Когда в растворе присутствуют несколько деполяризаторов, то каждая волна имеет хорошо выраженную площадку предельного тока, если потенциалы полуволны отдельных деполяризаторов различаются не менее, чем на 200 мВ.

Из уравнения (11), построив зависимость φ = f 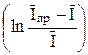, можно рассчитать число электронов, участвующих в элементарном акте разряда.

Если известно n, то, следовательно, известен и теоретический наклон прямой φ = f 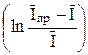для обратимой системы. При температуре 25 ^оС наклоны в случае одно, двух и трехэлектронного процессов равны соответственно 25,7; 12,8 и 8,6 мВ на единицу логарифма. Из указанной графической зависимости можно определить и потенциал полуволны, так как φ = φ_1/2 при 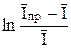=0.

Легко определить, что потенциалы, измеренные при ¼ и ¾ высоты волны, будут описываться уравнениями

φ_1/4 = φ_1/2 + 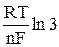, (12)

φ_3/4 = φ_1/2 – 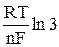. (13)

Из (12) и (13) следует, что полярографическая волна обратимого процесса симметрична относительно потенциала полувол­ны.

Разность между потенциалами ¼ и ¾ высоты волны при 25 ^оС равна

φ_1/4 – φ_3/4 = 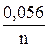. (14)

Таким образом, для одноэлектронного процесса она равна 56 мВ, для двухэлектронного – 28 мВ и т.д. Этот критерий позволяет быстро и точно оценить отклоняется ли исследуемый процесс от обратимого.

В случае, если реакция (2) не обратима, полярографическая волна как показал Я. Коутецкий, может быть представлена уравнением

φ = 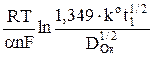+ 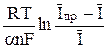= φ_1/2 + 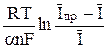, (15)

где φ_1/2 = 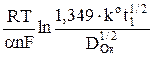– потенциал полуволны необратимых процессов;

k^o – константа скорости реакции, м/с; t₁ – период капания ртути, с; a – коэффициент переноса.

Из уравнения (15) следует, что потенциал полуволны необратимых процессов зависит от периода капания, а наклон прямой φ = f 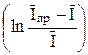больше, чем в случае обратимых волн.

По наклону полученной в эксперименте прямой или используя уравнение

φ_1/4 – φ_3/4 = 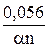, (16)

можно рассчитать величину an.

Измеряя зависимость потенциала полуволны от периода капания и используя уравнение

φ_1/2 = 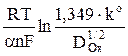+ 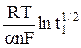, (17)

которое следует из определения φ_1/2, можно из наклона прямой φ_1/2 = f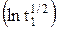

также рассчитать величину an, а, зная значение D_ox из независимых экспериментов, из первого слагаемого уравнения (17) – рассчитать константу скорости реакции.

ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ

Цель работы: освоить методику работы на полярографе и выполнить исследование восстановления ряда катионов для опреде­ления режима процесса, рассчитать коэффициенты диффузии и константы скорости.

Порядок выполнения работы

Общие положения.

1. Изучают методику работы на полярографе по его технической ин­струкции (прилагается).

2. Готовят растворы веществ для выполнения исследования по указанию преподавателя.

3. Тщательно моют все детали полярографической ячейки (см. рис.3) в на­чале водопроводной водой, затем теплой концентрированной H₂SO₄ марки «хч», затем снова водопроводной водой и, наконец, бидистилля­том. Капилляр сверху моют дважды перегнанной H₂SO₄, а затем большим количеством бидистиллята, подставив снизу широкий ста­кан.

4. Собирают ячейку и устанавливают высоту столба ртути такой, что­бы в бидистилляте период капанья был равен 6 –7 с.

5. В течение 15 мин пропускают водород одновременно через боко­вой сосуд Б и центральную часть ячейки А (см. рис. 3).

6. Закрывают кран между частями ячейки А и Б, в сосуд Б заливают исследуемый раствор и в течение 1 ч пропускают через него водород для удаления растворенного О₂. Водород всегда должен выходить из ячейки через гидравлический затвор.

7. Под давлением водорода переводят исследуемый раствор из сосуда Б в центральную часть А и заполняют этим раствором левую часть электролитического ключа (до крана, см. рис. 3). В правую часть электролитического ключа засасывают насыщенный раствор KCl из сосуда В. Исследуемый раствор в центральной части ячейки А до­полнительно продувают водородом в течение 10 мин.

8. Подсоединяют ячейку к измерительной схеме так, чтобы ртутная капля служила катодом, а вспомогательный электрод – анодом (см. рис.1).

9. Выполняют полярографическое исследование для одного из предложенных заданий.

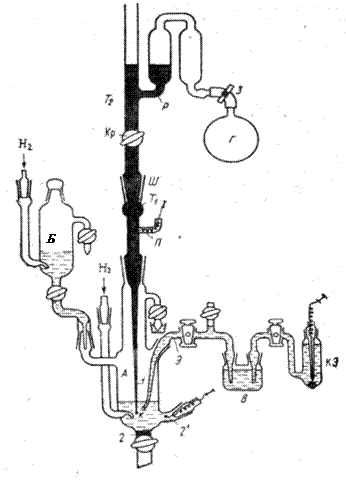Рис. 3. Рабочая схема полярографической ячейки:

А – центральная часть ячейка, в которую на шлифе Ш помещен капилляр (1); К – капля; 2 и 2' – ртутный или платино­вый аноды для поляризации; Б– боковой сосуд для освобождения раствора от кислорода воздуха; В –сосуд с насыщенным раствором KCl; Э – элекгролитический ключ (капилляр Луггина); З –зажим; Г–резиновая груша; Р – ртуть; Т₁ – трубка со ртутью, к которой припаян капилляр (I) и платино­вый контакт (П); Т₂– трубка со ртутью, снабженная краном (Кр) для перекрывания вытекания ртути из капилляра; КЭ – каломельный электрод сравнения

10. Определяют режим процесса и рассчитывают его кинетические характеристики.

Задание должно быть выполнено самостоятельно при условии получения консультации у преподавателя.

В работе должно быть выполнено одно из заданий.

А. Исследование электрохимической реакции в условиях лимитирующей стадии массопереноса на примере восстановления ионов свинца.

Б. Изучение кинетики разряда иона (Fe(CN)₆)^3- .

Необходимые растворы электролитов приготовьте согласно заданию, выданному преподавателем.

По результатам работы делают выводы и вычисляют абсолютную и относительную ошибки

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. В чем сущность полярографии?

2. Напишите уравнение полярографической волны.

3. Дайте описание обратимого и необратимого электродного про­цесса.

4. Рассчитайте константу скорости электродной реакции.

5. Каким способом можно установить кинетический режим протекания процесса?

6. Как выглядит график полярографической волны при восстановлении одного и двух веществ?

7. От каких параметров зависит величина полного предельного диффузионного тока?

8. Пояснить понятие предельного тока.

9. Проанализировать выражение (11) для обратимой полярографической волны.

10. Проанализировать выражение (15) для необратимой полярографической волны.

11. Пояснить понятия потенциала полуволны, три четверти и четверть волны.

12. Почему зависимость плотности тока от потенциала электрода имеет форму волны?

13. Какие величины можно определить, используя уравнение обратимой полярографической волны?

14. Какие величины можно определить, используя уравнение необратимой полярографической волны?

15. Написать и проанализировать уравнение связи потенциала электрода с активностями окисленной и восстановленной форм.

16. Размерности величин в уравнениях.

Работа 14