Второй закон термодинамики – включает в себя первое начало и позволяет судить о направленности процессов и положении равновесия

Вполне очевидно, что реакции с суммарным уменьшением энтальпии (экзотермические) могут идти самопроизвольно, как катящийся с горы камень. Однако хорошо известно, что самопроизвольно идут также некоторые реакции, сопровождающиеся увеличением энтальпии и охлаждением реактора (эндотермические).

Для характеристики эндотермических процессов и определения условий их самопроизвольного осуществления была введена новая функция состояния – энтропия. Изменение энтропии (ΔS) равно (по определению) минимальной теплоте, подводимой к системе в обратимом (все промежуточные состояния равновесны) изотермическом процессе, деленной на абсолютную температуру процесса:

S = Q_мин./T

На данном этапе изучения термодинамики следует принять как постулат, что существует некоторое экстенсивное свойство системы S, называемое энтропией, изменение которого так связано с процессами в системе:

В самопроизвольном процессе S > Q_мин./T

В равновесном процессе S = Q_мин./T

В несамопроизвольном процессе S < Q_мин./T

Для изолированной системы, где dq = 0, получим:

В самопроизвольном процессе S > 0

В равновесном процессе S = 0

В несамопроизвольном процессе S < 0

В общем случае энтропия изолированной системы или увеличивается, или остается постоянной.

Понятие энтропии возникло из полученных ранее формулировок второго закона (начала) термодинамики. Энтропия – свойство системы в целом, а не отдельной частицы.

Второе начало по У.Томсону (1851): "«в природе невозможен процесс, единственным результатом которого была бы механическая работа, совершенная за счет охлаждения теплового резервуара"»

По Р.Клаузиусу (1850): "«теплота сама по себе не может перейти от более холодного тела к более теплому"» или: "«невозможно сконструировать машину, которая, действуя посредством кругового процесса, будет только переносить теплоту с более холодного тела на более теплое"»

Самая ранняя формулировка второго начала термодинамики появилась раньше первого начала, на основании работы фр. С.Карно (1824) и ее математической интерпретации фр. Э.Клапейроном (1834) как КПД идеальной тепловой машины:

КПД = (T₁ –T₂)/T₁

Карно и Клапейрон сформулировали закон сохранения теплорода – невесомой неуничтожимой жидкости, содержание которой определяет температуру тела. Теория теплорода господствовала в термодинамике до середины XIX века, при этом законы и соотношения, выведенные на основе представлений о теплороде, оказались действительными и в рамках молекулярно-кинетической теории теплоты.

Второй закон термодинамики: в изолированной системе самопроизвольно протекающие процессы увеличивают энтропию системы.(На основании второго закона термодинамики возникла теория тепловой смерти Вселенной.)

В окружающем нас мире мы не всегда замечаем действие второго закона термодинамики, наблюдая высокую упорядоченность живых систем: в любой живой клетке всех животных и человека происходят тысячи упорядоченных по последовательности и во времени химических процессов. По расписанию ходят поезда, летают самолеты, работают люди и т.д. Высокая степень упорядоченности жизнедеятельности на Земле обязана, прежде всего, энергии Солнца. Нетрудно предугадать, что произойдет в том случае, если Земля лишится этого источника энергии. Следствие из второго закона термодинамики – высокая степень упорядоченности в системе возможна при поступлении энергии и вещества из-за пределов системы.

Третий закон термодинамики устанавливает, что энтропия физической системы при стремлении температуры к абсолютному нулю не зависит от параметров системы и остается неизменной. (В формулировке М. Планка энтропия S = 0 при T = 0 К.)

Проследим изменение энтропии по мере нагревания ионного кристалла. В идеальном ионном кристалле вблизи абсолютного нуля температуры существует наивысший порядок. Зависимость энтропии ионного кристалла от температуры (рис. 6.3).

Рис.6.3. Качественная зависимость энтропии ионного кристалла от температуры

Приведенный график демонстрирует, что энтропия жидкости обычно гораздо выше, чем энтропия твердого тела, а энтропия газа выше, чем энтропия соответствующей жидкости. Это означает, что с точки зрения второго закона термодинамики жидкостью быть более выгодно, чем твердым телом, а газом – выгоднее, чем жидкостью.

Таким образом, для самопроизвольного протекания реакции требуется, с одной стороны, уменьшение суммы энтальпий: если сумма энтальпий образования продуктов меньше суммы энтальпий образования реагентов, т.е. Н < 0, то такой процесс энергетически выгоден. С другой стороны, самопроизвольно может протекать лишь процесс, в котором сумма энтропий продуктов превышает сумму энтропий реагентов, т. е. изменение энтропии в ходе процесса должно быть положительным ( S > 0).

Энергия Гиббса

Возможно несколько вариантов изменения сумм энтальпий образования и энтропий веществ в ходе процесса.

1. Н < 0, S > 0. Процесс однозначно энергетически выгоден и может протекать самопроизвольно.

2. Н > 0, S < 0. Процесс однозначно энергетически невыгоден и не может протекать самопроизвольно.

3. Н < 0, S < 0. Уменьшение Н благоприятно для самопроизвольного протекания реакции, тогда как уменьшение S препятствует этому. (Неясно, возможно ли самопроизвольное протекание такой реакции.)

4. Н > 0, S > 0. Увеличение Н не способствует самопроизвольному протеканию реакции, однако возрастание S повышает ее вероятность. (Неясна возможность самопроизвольного протекания такой реакции.)

Роль арбитра, определяющего возможность самопроизвольного протекания реакции при постоянном давлении, играет энергия Гиббса:

G = Н – T S, где T – абсолютная температура, К.

Вычисление Δ_rG⁰ можно проводить также по уравнению, аналогичному тому, которое используется для расчета Δ_rН⁰

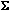
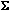
Δ_rG⁰= G_f ⁰ (прод.) – G_f ⁰(реаг.).

При G < 0 реакция может протекать самопроизвольно, а при G > 0 реакция термодинамически запрещена. Если G = 0, то реакционная система находится в состоянии равновесия (скорости прямой и обратной реакций равны).

Возможность самопроизвольной реакции в изолированной системе определяется сочетанием знаков энергетического (энтальпийного) и энтропийного факторов:

Знак ΔH	Знак ΔS	Возможность самопроизвольной реакции
+	-	Нет
-	+	Да
-	-	Зависит от соотношения ΔH и TΔ S
+	+	Зависит от соотношения ΔH и TΔ S

При изохорно-изотермическом процессе (V, T = const) может быть посчитан изохорно-изотермический потенциал А (энергия Гельмгольца). Расчёт полностью аналогичен расчету G.

Самопроизвольное протекание эндотермической реакции возможно лишь тогда, когда она сопровождается значительным увеличением энтропии. Примером такого процесса является взаимодействие гексагидрата дихлорида кобальта с хлористым тионилом, сопровождающееся ярко выраженным эндотермическим эффектом ( Н = +400 кДж/моль, наблюдается обледенение).

Уравнение реакции:

СоСl₂•6Н₂О + 6SOCl₂ = CoCl₂ + 6SO₂ + 12HCl

вскрывает причину протекания такого сильно эндотермического процесса: на 1 моль прореагировавшего кристаллогидрата образуется 18 моль (!) газообразных веществ.

Возможность или невозможность протекания реакции устанавливают с помощью уравнения Гиббса следующими способами.

1ля температуры 25 °С на основе табличных данных рассчитывают G⁰ по соотношению:

1 G⁰ = Н⁰– 298 S⁰.

2ля температуры, отличающейся от 25 °С, расчет проводят по соотношению:

1 G = G⁰ + RTlnK_р.

K_р при данной температуре можно найти, преобразовав выражение для равновесия

G = 0 G⁰ + RTlnK_р = 0

к виду:

Это соотношение позволяет получить значение константы равновесия при любой температуре.

Для окислительно-восстановительных реакций выражение для энергии Гиббса при стандартных условиях принимает следующий вид:

1 G⁰ = –nF ⁰,

где n – количество передаваемых электронов, F – постоянная Фарадея ( 96 500Кл/моль),
⁰ – ЭДС реакции. Из этого выражения следует, что реакция протекает при положительном значении ЭДС.

4. Из условия равновесия реакции ( G = 0) имеем: 0 = Н – T S.

Отсюда Т = Н/ S – температура, при которой реакция находится в состоянии равновесия.

Термодинамические расчеты позволяют оценить, например, возможность восстановления водородом некоторых элементов из их оксидов (табл. 6.2).

Таблица 6.2 Термодинамическая оценка возможности восстановления водородом элементов из их оксидов

Уравнение реакции	Н, кДж/моль	Температура, °С, при которой G = 0	Осуществление процесса на практике
MnO2 + 2H2 = Mn + 2H2O			Возможно
1/2Fe2O3 + 3/2H2 = Fe + 3/2H2O			Возможно
1/2Cr2O3 + 3/2H2 = Cr + 3/2H2O			Невозможно
SiO2 + 2H2 = Si + 2H2O			Невозможно
CaO + H2 = Ca + H2O			Невозможно

Термодинамика позволяет в принципе оценить возможность протекания химических реакций. Однако она ничего не говорит о реальных скоростях их протекания.

VII. КИНЕТИКА ХИМИЧЕСКИХ РЕАКЦИЙ

Предсказания химической термодинамики наиболее верны в своей «запрещающей» части. Если, например, для реакции

N₂ + O₂ = 2 NO ΔG⁰ = +176 кДж,

то эта реакция не пойдет самопроизвольно, и никакой катализатор ей не поможет. Известный заводской процесс получения NO из воздуха требует огромных затрат энергии и неравновесного проведения процесса.

С другой стороны, далеко не все реакции, для которых ΔG < 0, «спешат» осуществиться на практике. Куски каменного угля могут веками лежать на воздухе, хотя для реакции

C + O₂ = CO₂ ΔG⁰ = -395 кДж

Предсказание скорости химической реакции, а также выяснение зависимости этой скорости от условий проведения реакции осуществляет химическая кинетика – наука о химическом процессе, его механизме и закономерностях протекания во времени.

Скорость химической реакции – это изменение концентрации какого-либо из реагирующих веществ в единицу времени при неизменном объёме системы в случае гомогенной реакции.

Скорость химической реакции определяется как изменение концентрации одного из участвующих в реакции веществ (исходное вещество или продукт реакции) в единицу времени. Содержание всех остальных может быть найдено из уравнения реакции.

Скорость не является постоянной, она изменяется во времени. Различают среднюю и истинную.

V_ср. = ± ((С₂ – С₁) / (τ₂ –τ ₁)) = ± (DС / D τ)

где С₁ и С₂ –молярные концентрации веществ в моменты времени τ ₁ и τ ₂ соответственно (знак (+) – если скорость определяется по продукту реакции, знак (–) – по исходному веществу).

V_ист. = ± dс / d τ, Δτ → 0

Изменение концентрации за бесконечно малый промежуток времени.

Скорость не бывает отрицательной величиной, концентрации берут по модулю.

Реакции происходят при столкновении молекул реагирующих веществ. Ее скорость определяется количеством столкновений и вероятностью того, что они приведут к превращению. Число столкновений определяется концентрациями реагирующих веществ, а вероятность реакции – энергией сталкивающихся молекул.

Факторы, влияющие на скорость химических реакций:

1) природа реагирующих веществ;

2) концентрация веществ;

3) температура;

4) наличие катализатора;

5) другие факторы, например: давление.

1. Природа реагирующих веществ. Большую роль играет характер химических связей и строение молекул реагентов. Реакции протекают в направлении разрушения менее прочных связей и образования веществ с более прочными связями. Так, для разрыва связей в молекулах H₂ и N₂ требуются высокие энергии; такие молекулы мало реакционноспособны. Для разрыва связей в сильнополярных молекулах (HCl, H₂O) требуется меньше энергии, и скорость реакции значительно выше. Реакции между ионами в растворах электролитов протекают практически мгновенно.

Примеры

Фтор с водородом реагирует со взрывом при комнатной температуре, бром с водородом взаимодействует медленно и при нагревании.

Оксид кальция вступает в реакцию с водой энергично, с выделением тепла; оксид меди – не реагирует.

2. Концентрация. С увеличением концентрации (числа частиц в единице объема) чаще происходят столкновения молекул реагирующих веществ -–скорость реакции возрастает.

Закон действующих масс (К. Гульдберг, П.Вааге, 1867г.) – основной закон кинетики.